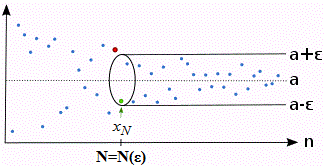
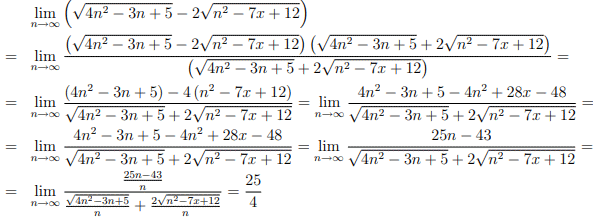Число a называется пределом числовой последовательности {xn}, если для любого как угодно малого положительного числа ε>0 найдется натуральное число N=N(ε), такое что при всех n>N выполняется неравенство |xn-a|<ε.
Если a является пределом последовательности то этому соответствует запись
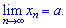
Вычисление предела числовой последовательности
Пример 1 Легкое задание, которое учит выносить доминантные множители в дробях, которые дают наибольший вклад при номере, стремлящемся к бесконечности, и упрощать на них
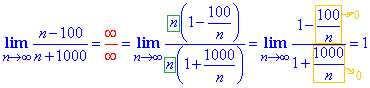
В этом вся сложность алгоритма вычисления предела последовательности при переменной стремящейся к бесконечности, но бывают исключения, о которых поговорим делее.
Если последовательность сходится, то она имеет конечный лимит. Если предел равен бесконечности, то говорят, что такая последовательность расходится.
Для установления сходимости последовательностей нужно хорошо уметь находить пределі, что мы с Вами постоянно совершенствуем.
Пример 2 Имеем неопределенность вида бесконечность минус бесконечность (∞-∞), поэтому теорему о разнице пределов здесь применять нельзя. Преобразуем выражение, умножением и делением на сопряженное выражение. Для вычисления значения предела упрощаем дробь на выражение, что вносит наибольший вклад при аргументе стемящемся к бесконечности. Как выносить множители из под корня Вы должны научиться самостоятельно, без этого трудно будет раскрывать пределы с корнями.
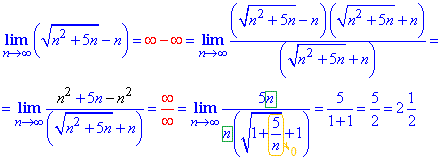
Пример 3 Разницу корней в знаменателе дроби не уножаєм на сопряженное выражение, а просто номер n выносим из под корня (внимательно посмотрите как это делать), а дальше упрощаем с n выделенным в числителе
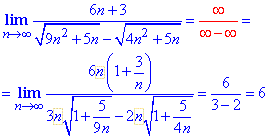
Пример 4 Последовательность из частки иррациональных выражений имеет конечную границу, если степень номера n в знаменателе равен степени в числителе (или больше). Его выделяем по указанной в методике формуле, и упрощаем
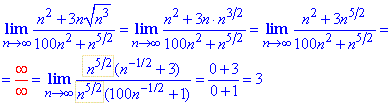
Пример 5 Найти предел последовательности 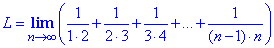
Вычисления: Проанализировав, как меняются слагаемые для всех номеров k=2,3,4 можем записать формулу
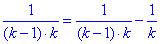
Таким образом исходную сумму сводим к виду
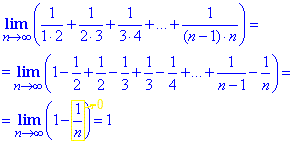
Единого устоявшегося алгоритма, как раскрывать такие суммы нет. Порой можно увидеть простые схемы чередования слагаемых, в других заданиях бывает нужно вычислить суммы арифметических или геометрических прогрессий. Лишь бы оценить сверху, что последовательность ограничена, и к какому значению стремится.
Пример 6 Лимит последовательности из частки показательных выражений вычисляют путем выделения и упрощения доминантных множителей в числителе и знаменателе дроби. В заданном лимите основания равны 2 и 4, их можно свести к общему 4 в (высшем) степени ровному n. Все остальное и даст значение к которому стремится дробь.
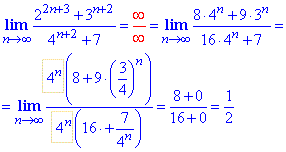
Пример 7 Предел последовательности из разности бесконечно больших дробей раскрываем методом сведения их к общему знаменателю и упрощения в числителе и знаменателе множителя, что вносит главный вклад
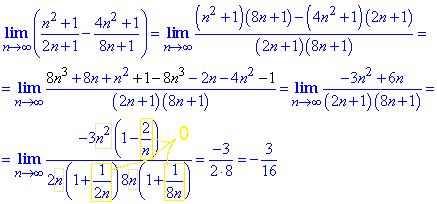
Пример 8 Найти лимит последовательности
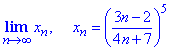
Вычисления: Представим общий член последовательности {xn} в виде
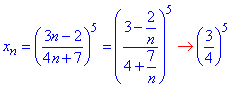
По теореме о границе показательной функции, она равна показателю от границы основы, если степень конечна. Отсюда lim{xn}=(3/4)^5.
Пример 9 В такого сорта заданиях вынесения n в главной степени за скобки в числителе и знаменателе дроби к упрощению не приведет. Попробуйте проверить самостоятельно, остается взглянуть в формулы сокращенного умножения и расписать разницы и суммы в кубе и в четвертой степени по следующим формулам
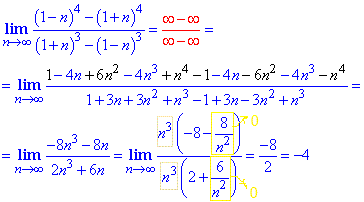
Таким образом, получим слагаемые с противоположными знаками, которые в сумме дадут 0, остальные слагаемые в предельном переходе упростятся по приведенной выше методике.
И напоследок, еще несколько решений на предел последовательности, которые предлагаем разобрать самостоятельно.
10 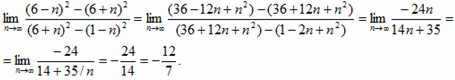
11 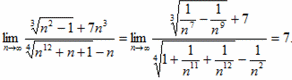
12 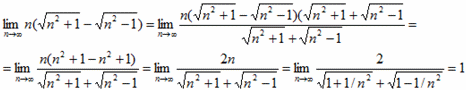
13