Знаходження границь займає вагоме місце в курсі вищої математики. Для цього потрібно знати чимало правил та прийомів. Про все це піде мова в даному розділі та для початку дамо означення границі числової послідовності.
Означення числової послідовності: Множину чисел 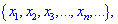
 яка визначена для кожного натурального числа за однаковим правилом називають числовою послідовністю і позначають {xn}, де x1,x2,x3,... – члени числової послідовності, xn– загальний член послідовності.
яка визначена для кожного натурального числа за однаковим правилом називають числовою послідовністю і позначають {xn}, де x1,x2,x3,... – члени числової послідовності, xn– загальний член послідовності.
Означення границі послідовності: Число a називається границею числової послідовності {xn}, якщо для будь-якого як завгодно малого додатного числа 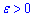 знайдеться таке натуральне число
знайдеться таке натуральне число 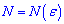 , таке що при всіх n>N виконується нерівність
, таке що при всіх n>N виконується нерівність
Якщо a є границею послідовності то записують
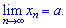
Є декілька типів числових послідовностей, які ви обов'язково повинні знати:
1) Зростаюча послідовність – кожен її член більший від попереднього
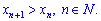
2) Неспадна послідовність – кожен наступний член не менший від попереднього
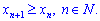
3) Спадна послідовність – кожен новий член менший за попередній
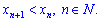
4) Незростаюча послідовність – кожен старший член не більший за попередній
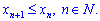
5) Обмежена послідовність має місце тоді, коли знайдуться такі дійсні числа m і M, що для всіх натуральних чисел 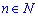 виконується нерівність
виконується нерівність 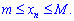
6) Послідовність {xn} називається необмеженою, якщо вона постійно або зростає або спадає.
7) Послідовність, що має границю називається збіжною. Протилежна до неї послідовність – відповідно розбіжною.
ВЛАСТИВОСТІ ЗБІЖНИХ ПОСЛІДОВНОСТЕЙ
1) Границя сталої послідовності рівна сталій.
2) Якщо послідовність має границю, то границя єдина. Звідси слідує, що така послідовність обмежена.
3) Нехай границя числової послідовності існує і рівна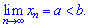
Тоді знайдеться таке число N, що для всіх більших за нього значень n>N виконується нерівність xn<b.
4) Припустимо, що виконується нерівність
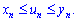
Якщо послідовності {xn} та {yn} збіжні та їх границі рівні
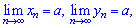
то послідовність {un} також буде збіжною, а її співпадатиме з границями бокових послідовностей
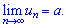
5) Будь-яка монотонно обмежена послідовність має границю.
Частковим випадком числових послідовностей є арифметична та геометрична прогресії.
Одними з простих завдань є визначення формули загального члена послідовності за відомими першими. Для прикладу, виберемо такі задачі із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Написати формулу загального члена послідовності.
1) (4. 258) 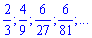
Розв'язок. При визначенні загального члена послідовності слід вловити особливість зміни наступного його члена до попереднього. Різниця між ними може носити лінійний, показниковий чи інший характер. В даному випадку приклади не важкі, оскільки кожен наступний член описаний в тому вигляді, в якому його визначають, а не у вигляді дробу (в чисельнику і знаменнику одне число). Варто зазначити те, що при виведенні загального члена послідовності прийнято записувати першими змінні n, тобто у вигляді
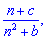
а не
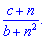
Перейдемо до знаходження шуканих величин.
З особливості зміни чисельника і знаменника
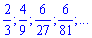
бачимо, що чисельник зростає лінійно, а знаменник за показниковим законом.
Загальний член послідовності записуэмо формулою
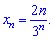
В чисельнику отримали лінійну залежність, знаменнику - показникову.
2) (4. 261) 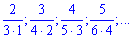
Розв'язок. В цьому завданні і чисельник і знаменник змінюються лінійно, зміщуючись від одиниці на певні константи. Тільки в знаменнику маємо добуток чисел, тому в формлі загального члена
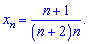
це виражається квадратичною залежністю.
3) (4. 265) 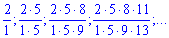
Розв'язок.В даному прикладі зміна чисельника та знаменника є нелінійною, проте загальний член послідовності вловити можна.
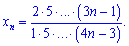
Для знаходження формули загального члена послідовності дослідіть поведінку окремо чисельника та знаменника. Визначте чи вони змінюються лінійно, нелінійно, степенево і т.д. На основі закономірностей виведіть формулу загального члена послідовності. Це вся інструкція при виведенні формули загального члена послідовності. Спочатку буде важкувато, зато пысля вправлянь будете малювати загальний член як художни картину.


