Теорія границь - один з розділів математичного аналізу, який одним під силу освоїти, інші з труднощами обчислюють границі. Питання знаходження границь є досить загальним, оскільки існують десятки прийомів знаходження границь різних видів. Одні і ті ж границі можна знайти як за правилом Лопіталя, так і без нього. Буває, що розклад в ряд безмежно малих функцій дозволяє швидко отримати потрібний результат. Існує набір технік, що дозволяють знайти границю функції будь-якої складності. В даній статті спробуємо розібратися в основних типах границь, які найбільш часто зустрічаються на практиці. Теорію та означення границі ми тут давати не будемо, в інтернеті безліч ресурсів де це розжовано. Тому перейдемо до практики обчислення границь, саме тут у Вас і починається "не знаю! не вмію! нас не вчили!"
Обчислення границь методом підстановки
Приклад 1. Знайти границю функції
Lim((x2-3*x)/(2*x+5), x=3).
Розв'язання: Такого типу приклади обчислюють звичайною підстановкою
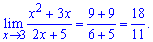
Границя рівна 18/11.
Нічого складного і мудрого в таких границях немає, підставили значення, обчислили, записали границю у відповідь. Зате на базі таких границь всіх привчають, що перш за все потрібно підставити значення у функцію (принаймі перевірити, що отримаємо? чи - до чого прямує границя?).
Далі границі ускладнюють, вводять поняття безмежності, невизначеності і т.д.
Границі з невизначеністю типу безмежність розділити на безмежність. Методи розкриття невизначеності
Приклад 2. Знайти границю функції
Lim((x2+2x)/(4x^2+3x-4), x=infinity).
Розв'язання: Задана границя виду поліном розділити на поліном, причому змінна прямує до безмежності
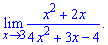
Проста підстановка значення до якого прямує змінна знайти границю не допоможе, отримаємо невизначеність виду безмежність розділити на безмежність.
Алгоритм обчислення границі полягає у знаходженні найбільшого степеня "ікс" в чисельнику чи знаменнику. Далі на нього спрощують чисельник і знаменник і знаходять границю
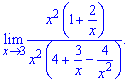
Оскільки значення 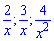 прямують до нуля при змінній прямуючій до нескінченності то ними нехтують, або записують в кінцевий вираз у вигляді нулів
прямують до нуля при змінній прямуючій до нескінченності то ними нехтують, або записують в кінцевий вираз у вигляді нулів
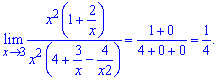
Зразу з практики можна отримати два висновки, які є підказкою в обчисленнях. Якщо змінна прямує до нескінченності і найбільший степінь чисельника перевищує найбільший степінь знаменника то границя рівна нескінченності (+ чи -, знак потрібно уточняти). В протилежному випадку, якщо вираз в знаменнику старшого порядку ніж в чисельнику границя рівна нулю.
Формулами границі можна записати так
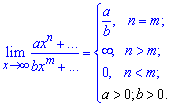
Якщо маємо в границі звичайний поліном без дробів, то границя теж рівна нескінченності
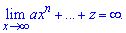
Наступний тип прикладів на границі базується на поведінці функції біля нуля.
Приклад 3. Знайти границю функції
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Розв'язання: Тут вже виносити найстарший доданок полінома не потрібно. З точністю до навпаки, необхідно знайти найменший степінь чисельника і знаменника та тільки їх і врахувати при обчисленні границь
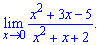
Значення x^2; x прямують до нуля коли змінна прямує до нуля  Тому ними нехтують, таким чином отримаємо
Тому ними нехтують, таким чином отримаємо
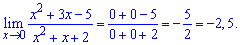
Границя рівна 2,5.
Границі з невизначеністю типу 0/0 і методи їх обчислень
Зразу всі згадують правило, що ділити на нуль не можна. Однак в цьому контексті маємо на увазі безмежно малі функції.
Розглянемо для наочності приклад
Приклад 4. Знайти границю функції
Lim((3x^2+10x+7)/(x+1), x=-1).
Розв'язання: При підстановці у знаменник x=-1 отримаємо нуль, також 0 отримаємо в чисельнику. Отже маємо невизначеність типу 0/0.
Боротися з такою невизначеністю просто: потрібно розкласти квадратний тричлен на множники, а точніше - виділити множник, який перетворює вираз на нуль.
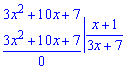
Отже, границю можна записати у вигляді
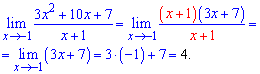
Ось і вся методика. Подбним чином поступаємо, якщо маємо границі частки многочленів третього та вищого степеня.
Приклад 5. Знайти границю функції
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Розв'язання: Пряма підстановка показує
2*4-7*2+6=0;
3*4-2-10=0
що маємо невизначеність типу 0/0.
Поділимо квадратний тричлен на множник, що дає особливість
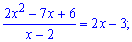
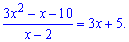
Є практики, які вчать, що многочлени 2 порядку, тобто квадратні тричлени, слід розв'язувати через дискримінант. Але сам факт, що в точці прямим підставленням отримуємо нуль прямо вказує, що вона є розв'язком, іншу дістанемо роздленням вільного члена на неї. Тобто, при "ікс" прямуючому до 2 в чисельнику отримали 0, тоді вільний член =6 ділимо на 2 і отримаємо, що другий корінь квадратного тричлена =6/2=3.
Обчислення дискримінанту і коренів не є доцільним в план затраченого часу в порівнянні з методом запропонованим вище, тому позбувайтеся особливості у границі за вказаним алгоритмом.
Записуємо розклад квадратного тричлена на множників та розписуємо границю
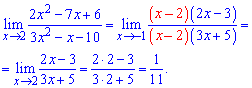
Як бачите, нічого складного в розкритті таких границь немає. Якщо задають частку многочленів вищого порядку за 2, то на момент вивчення границь Ви знаєте, як їх длити на одночлен, принаймі за програмою мали вже пройти. Серед завдань на невизначеність типу 0/0 зустрічаються такі, в яких потрібно застосовувати формули скороченого множення. Але якщо Ви їх не знаєте, то діленням многочлена на одночлен можна отримати потрібну формулу
Приклад 6. Знайти границю функції
Lim((x^2-9)/(x-3), x=3).
Розв'язання: Маємо невизначеність типу 0/0. В чисельнику застосовуємо формулу скороченого множення
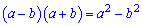
і обчислюємо потрібну границю
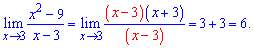
В результаті розкриємо невизначеність та отримаємо 6.
Метод розкриття невизначеності множенням на спряжене
Метод застосовують до границь, в яких невизначеність породжують ірраціональні функції. Чисельник або знаменник перетворюється в точці знаходження границі в нуль і невідомо як розкривати особливість 0/0.
Приклад 7. Знайти границю функції
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Розв'язання: Подамо границю у вигляді формули
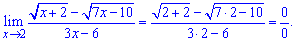
При підставленні значення x=2 отримаємо невизначеність типу 0/0.
Схема розкриття даної особливості полягає у множенні ірраціонального виразу, що її містить, на спряжене. Щоб вираз не змінився знаменник потрібно поділити на таке ж значення
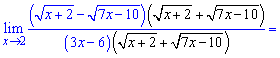
За правилом різниці квадратів перетворюємо чисельник та обчислюємо границю
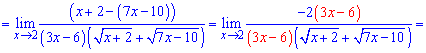
Спрощуємо доданки, що вносять особливість в границю та виконуємо підставлення
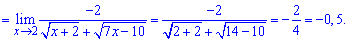
Вкінці залишиться обчислити корені квадратні в знаменнику та спротити дріб.
Приклад 8. Знайти границю функції
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Розв'язання: Границя має особливість виду 0/0.
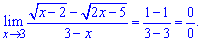
Для розкриття множимо і ділимо на спряжений вираз
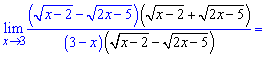
Записуємо різницю квадратів
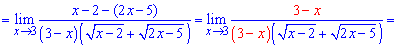
Спрощуємо доданки, що вносять особливість та знаходимо границю
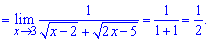
Достатньо простий прикад розкриття особливості методом позбуття ірраціональності.
Приклад 9. Знайти границю функції
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Розв'язання: Підставимо двійку в границю.
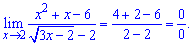
Отримаємо невизначеність 0/0.
Знаменник потрібно домножити на спряжений вираз, а в чисельнику розкласти квадратний тричлен шляхом розв'язку відповідного квадратного рівняння. Оскільки відомо, що 2 є коренем, то другий корінь знаходимо за теоремою Вієта
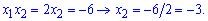
Таким чином чисельник запишемо у вигляді
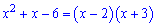
та підставимо у границю
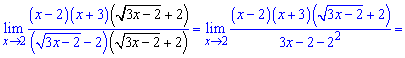
Звівши різницю квадратів позбуваємося особливості в чисельнику і знаменнику
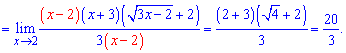
Наведеним чином можна позбутися особливості в багатьох прикладах, а застосування правила треба передбачатии всюди, де задають різницю коренів, що перетворюється в нуль при підстановці. Інші типи границь містять показникові функції, нескінченно малі функції, логарифми, особливі границі і т.д., та нові для Вас методики розкриття. Про це Ви зможете прочитати в наведених далі уроках на границі.
Обчислення границь в Мейплі
Даний матеріал корисний перш за все для студентів. Можливо в програмі навчання, а дехто для себе вивчає математичні програми та пакети, які дозволяють полегшити ручні розрахунки і перевірки розв'язків, автоматизувати обчислення.
Це можуть бути математичні пакети MathСad, Мathematica, Maple, MatLab.
Обчислення границь в Мейплі досить просто організувати навіть новачку.
Все, що потрібно - правильно ввести функцію, границю якої знаходимо.
> restart;
Границя першої функції в Мейпл матиме наступний запис.
Тиснемо вкінці набраного коду "Enter" і отримаємо кінцеве значення границі
> limit((x^2+3*x)/(2*x+5),x=3); 18/11
Границю другої функції отримаємо із запису
> limit((x^2+2*x)/(4*x^2+3*x-4),x=infinity); 1/4
Третій приклад прийме наступний вигляд:
> limit((x^2+3*x-5)/(x^2+x+2),x=infinity); 1
Мейпл без проблем знаходить першу чудову границю
> limit(sin(x)/x,x=0); 1
та другу чудову границю
> limit((1+1/x)^x,x=infinity); exp(1).
Фрагмент обчислення границь в математичному пакеті Мейпл наведено нижче
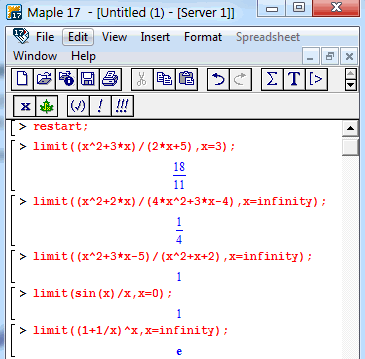 В наступних публікаціях проаналізовано готові відповіді до понад 200 прикладів на границі.
В наступних публікаціях проаналізовано готові відповіді до понад 200 прикладів на границі.
Матеріал в повній мірі відповідає вимогам ВУЗ-ів та доможе вивчити тему самому лінивому студенту.
Головне - не спішіть, а уважно перечитуйте все що написано.
Решта перетворень містять формули, які розписані до дрібниць.


