Швидким способом знаходження границь функцій, що мають особливості виду нуль на нуль {0/0} є застосування еквівалентних нескінченно малих функцій. Вони вкрай необхідні, якщо потрібно знаходити границі без застосування правила Лопіталя. Еквівалентності полягають в заміні функції її розкладом в ряд Маклорена. Як правило, при обчисленні границь використовують не більше двох членів розкладу. Для зручності наведемо еквівалентності основних функцій при прямуванні змінної до нуля 
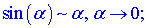
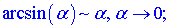
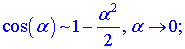
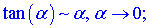
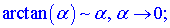
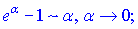
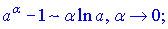
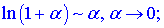
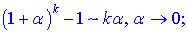
є ще кілька формул, проте вони зустрічаються рідко.
Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" для закріплення практичних знань.
Приклад 1. Знайти границі функцій.
1) (5. 492. 1) 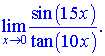
Розв'язок. Згідно правил розкладу в околі нуля поведінка синуса та тангенса буде наступною
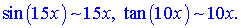
На основі розкладу обчиюємо границя
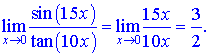
З формул бачимо, що це набагато швидше, ніж зводити до першої чудової границі (sin(15x)/(15x); 10x/tan(10x)).
2) (5. 492. 7) 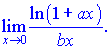
Розв'язок. На основі правил еквівалентності
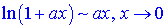
границя прийме значення
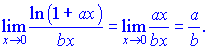
3) (5. 492. 8) 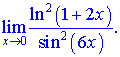
Розв'язок. Замінимо логарифм та синус їх розкладом в околі нуля
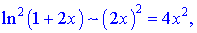
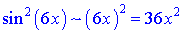
та підставимо у границю
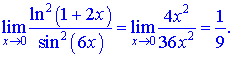
В результаті отримаємо 1/9.
4) (5. 492. 9) 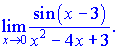
Розв'язок.Якщо Вам зустрічаються подібні приклади то потрібно виконати наступне. На основі формул розкладу спростити чисельник
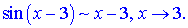
Підстановкою в границю отримаємо невизначеність типу (0/0).
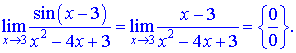
Для її розкриття потрібно розкласти квадратичну функцію на прості множники.
Щоб не розв'язувати квадратне чи інші рівняння, які можуть бути задані, можете сміло ділити знаменник на чисельник
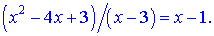
Підставляємо в границю і знаходимо
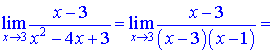
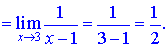
Такого роду приклади задумані так, що знаменник і чисельник мають особливості, позбувшись яких без проблем обчислюємо границю.
5) (5. 492. 11) 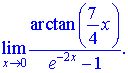
Розв'язок.За правилами еквівалентних нескінченно малих фунцій арктангенс і експоненту заміняємо першими членами розкладу в ряд в околі нуля
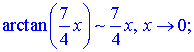
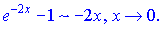
Далі підставляємо в функцію та обчислюємо границю
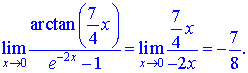
В інший спосіб обчислення прикладу займе цілий урок та прийдеться застосовувати кілька граничних теорем.
6) (5. 492. 13)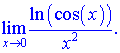
Розв'язок. Проводимо заміну функцій еквівалентними розкладами
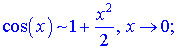
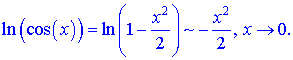
На основі цього отримаємо
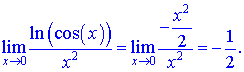
границю, яка рівна -1/2.
7) (5.492.15) 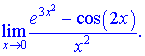
Розв'язок.Для застосування правил еквівалентності додамо і віднімемо в чисельнику одиницю.
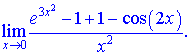
Далі запишемо розвинення експоненти і косинуса
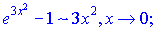
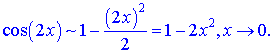
та підставимо в дробову функцію
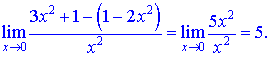
В підсумку отримаємо 5.
8) (5. 492. 17) 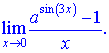
Розв'язок. Перетворимо чисельник за формулою
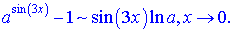
замінимо показникову функцію та зведемо до першої визначної границі
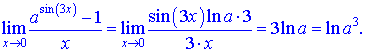
9) (5. 492. 19) 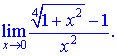
Розв'язок. Згідно розкладу кореневої функції в околі нуля отримаємо
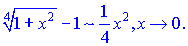
Границя перетвориться до частки квадратичних функцій
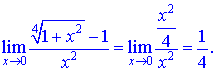
Застосування еквівалентних функцій дозволяє швидко знаходити границі показникових, тригонометричних та інших функцій. Використовуйте їх в тих випадках коли це необхідно, вивчайте та збагачуйте знання самостійним розв'язуванням. Це дозволить Вам бути спокійними та впевненими при написанні контрольних робіт, тестів.
Переглянути подібні матеріали


