Ефективним способом знаходження границь функцій, які мають особливості типу безмежність розділити на безмежність ∞/∞ чи нуль розділити на нуль 0/0 є застосування правила Лопіталя:
Теорема: Границя відношення двох нескінченно малих або двох нескінченно великих функцій рівна границі відношення їх похідних, якщо такі існують
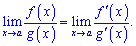
І не важливо, до якого значення прямує аргумент, головне отримати одну з вказаних особливостей. Якщо після однократного використання правила Лопіталя знову отримаємо особливість виду 0/0 або ∞/∞ то правило необхідно застосовувати повторно, і так аж до того часу, доки не позбудемося особливості.
Розкриття невизначеностей виду нескінченність мінус нескінченність, нуль помножити на нескінченність, нуль в степені нескінченність або навпаки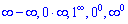 
зводиться до розглянутих вище невизначеностей за наведеною далі схемою.
Якщо одна функція прямує до нуля f(x)→0, а друга до безмежності g(x)→∞ при змінній прямуючій до певного значення x→a, то для застосування правила Лопіталя необхідно виконати наступні перетворення
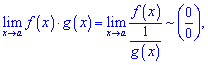
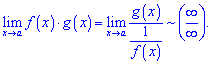
У випадку трьох останніх невизначеностей (1*∞, 0^∞, 0^0 ) потрібно застосовувати метод логарифмування
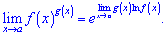
На практиці логарифмування є ефективним способом розкриття границь, хоча мало студентів його на повну використовують. Наприкінці цієї статті та в наступній такі завдання ми наводимо, тож можете переглянути схеми обчислень.
Правило Лопіталя. Розкриття невизначеностей 0/0 та ∞/∞
Щоб зекономити на час загрузки сторінки і дати максимумальну клькість готових прикладів до деяких завдань умову пропустимо, а наведемо алгоритм обчислення границі
Приклад 1 Перше завдання на першу важливу границю. Вона відповідає першому правилу Лопіталя, коли маємо частку двох нескінченно малих функцй, тобто особливість виду 0/0. Для розкриття особливості продиференціюємо чисельник та знаменник дробу, а далі підставимо значення аргумента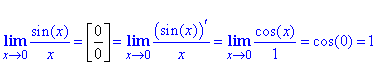
Аналогчний результат можна отримати через еквівалентні нескінченно малі величини, але це вже друга не менш ефективна методика знаходження границь.
Приклад 2 Знайти границю функції користуючись правилом Лопіталя та не застосовуючи його
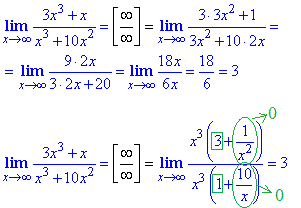
Для розкриття невизначеності типу ∞/∞ двічі (самостійно тричі) знаходимо похідні чисельника та знаменника дробу, а далі спрощуємо отриманий вираз.
Якщо правилом Лопіталя користуватися не можна, то маємо змінну,що прямує до безмежності, тому з чисельника та знаменника дробу виносимо множники, які вносять найбльший вклад. Далі оцінюємо вирази, що залишилися в дужках та знаходимо кінцеве значення границі.
Приклад 3 Для частки нескінченно малих функцій, що дають невизначеність типу 0/0 один раз застосуємо правило Лопіталя
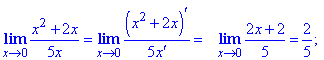
Приклад 4 Маємо частку двох нескінченно малих функцій tan(x)-sin(x) та x^3 при аргумент прямуючому до нуля
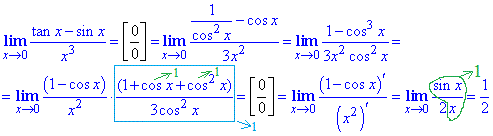
Для розкриття особливості виду 0/0 повторно використали формулу Лопіталя та розклали в чисельнику різницю кубів за формулами скороченого множення.
Приклад 5 Двічі застосувавши правило Лопіталя, позбуваємося невизначеності типу ∞/∞.
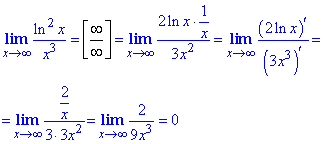
Приклад 6 Частка ln(x)/cot(x) дає невизначеність типу безмежність розділити на безмежність ∞/∞ при змінній прямуючій до нуля. Обчислюємо ліміт за правилом Лопіталя шляхом диференціювання чисельника та знаменника дробу
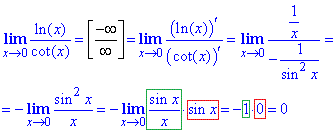
Далі виділяємо першу важливу границю та множник, що прямує до нуля.
Приклад 7. Часто правило Лопіталя ефективно застосовувати коли маємо показникові функції в чисельнику чи знаменнику дробу.
Знайдемо похідну чисельника та знаменника за змінною та виконаємо граничний перехід
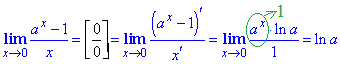
Розглянемо декілька прикладів із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" на застосування правила Лопіталя.
Приклад 8 (5.626) Знайти границю
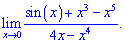
Розв'язування: Підстановкою встановлюємо, що маємо невизначеність виду нуль на нуль (0/0). Щоб її позбутися застосуємо правило Лопіталя
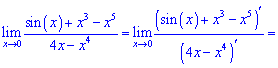
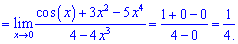
Границя функції рівна 1/4.
Приклад 9 (6.629) Обчислити границю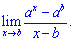 
Розв'язування: Як і у попередньому прикладі маємо невизначеність типу (0/0). За правилом Лопіталя обчислюємо похідну окремо чисельника і знаменника
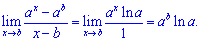
Другий доданок в чисельнику є сталою, тому його похідна рівна нулю.
Приклад 10 (6.634) Знайти границю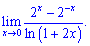 
Розв'язування: Враховуючи особливість (0/0) застосовуємо формулу Лопіталя
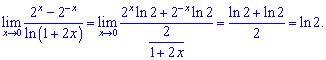
Показникові функції в нулю рівні одиниці, тому залишаться тільки логарифми.
Приклад 11 (4.639) Обчислити границю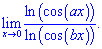 
Розв'язування: Розкриваємо невизначеність виду (0/0)
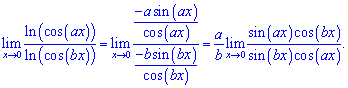
Чисельник та знаменник перетворимо до суми синусів на основі правила добутку
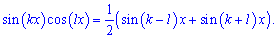
В результаті запишемо чисельник і знаменник через формули
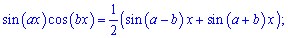
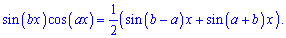
Підставимо знайдені значення в границю
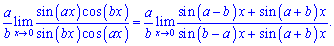
Знову отримали особливість 0/0, тому повторно застосовуємо правило Лопіталя
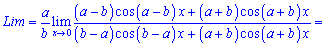
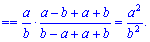
Похідна від синуса рівна косинусу, ну і осільки маємо складену функцію то множимо на похідну від залежності під синусом. При граничному переході враховано, що косинус функція прямує до одиниці при змінній, що прямує до нуля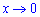 
.
Приклад 12 (4.645) Знайти границю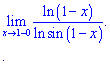 
Розв'язування: Маємо особливість виду безмежність розділити на безмежність ∞/∞.
Знайдемо похідні логарифмів
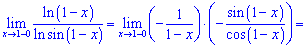
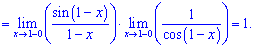
Після підстановки отримаємо дві функції, одну з яких знаходимо через першу чудову границю.
Приклад 13 (4.668)Знайти границю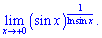 
Розв'язування: Зводимо функцію під формулу другої чудової границі
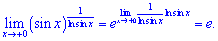
Отримали у результаті обчислень експоненту.
Метод логарифмування. Розкриття невизначеностей ∞^0, 0^0, 1^∞
Приклад 14 Знайти границю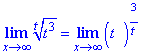 
Розв'язування: Маємо невизначеність типу безмежність в нульовому степені. Позначимо y=(t3 )1/t та про логарифмуємо
ln(y)=3ln(t)/t.
далі за правилом Лопіталя обчислюємо
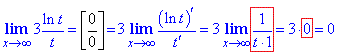
Відновлюємо границю
ln(y)=0→y=e0=e.
Приклад 15 Обчислити границю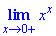 
Для обчислення границі використаємо логарифмування, для цього позначимо за нову функцію y=xx, і від логарифма ln(y) знайдемо ліміт.
ln(y)=ln(xx)= x•ln(x).
Знайдемо границю функції за правилом Лопіталя
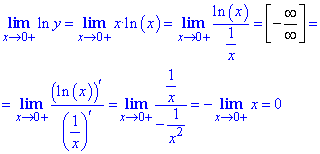
Повернемося до заміни функцій
ln(y)=0→y=e0=e.
Решта 15 готових прикладів, які більш повно розкривають метод логарифмування та правило Лопіталя ви знайдете у наступній статті.
Застосуванням правила Лопіталя швидко та ефективно можна розкрити невизначеності виду 0/0 та ∞/∞. Користуйтеся формулою Лопіталя на практиці і Вам не буде важко знаходити подібні границі у навчанні.
Переглянути подібні матеріали
