Арифметична та геометрична прогресія не буде для Вас складною темою після перегляду завдань із "Збірника задач для вступників. Математика" виданого Волинським державним університетом імені Лесі Українки у 2001 році. Уважно перегляньте відповіді 2 рівня складності та виберіть для себе найнеобхідніше. Якщо наведені приклади для Вас важкі, прочитайте для початку прості задачі на арифметичну та геометричну прогресію (1 рівень).
Група Б (рівень 2)
Приклад 1. В арифметичній прогресії а8=12,4; a23=4,7. Обчислити суму а14+a17.
Розв'язання: Представимо 14 член прогресії через 8 та 17 через 23. У формулах вони матимуть запис
a14=а8+6d;
a17=a23-6d.
Знаходимо шукану суму членів прогресії
a14+a17=a8+6d+a23-6d=a8+a23;
a14+a17=12,4+4,7=17,1.
Відповідь: сума рівна 17,1.
Приклад 2. У геометричній професії b4=3; b17=14,7. Обчислити добуток b9*b12.
Розв'язання: Враховуючи властивості геометричної прогресії, запишемо її 9 член через 4 та 12 через 17.
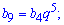
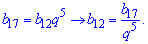
Бачимо, що при множенні знаменник геометричної прогресії спрощується
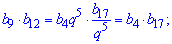
b9*b14=3*14,7=44,1.
Відповідь: добуток рівний 44,1.
Приклад 3. Сума n перших членів арифметичної прогресії виражається формулою Sn=3n2+6n. Обчислити a6.
Розв'язання: Знайдемо перший член прогресії та суму двох
a1=S1=3+6=9;
a1+a2=2a1+d=S2=3*2^2+6*2=24.
З другого рівняння, враховуючи значення першого члену, знаходимо крок прогресії
d=24-2a1=24-2*9=6.
За загальною Формулою Обчислюємо 6 член арифметичної прогресії
a6=a1+5d=9+5*6=39.
Відповідь: a6=39.
Приклад 4. Сума n перших членів арифметичної прогресії виражається формулою Sn=n2+5n. Обчислити a10.
Розв'язання: Завдання ідентичне попередньому, тільки цього разу спробуємо розв'язати за іншою методикою. Використаємо суму арифметичної прогресії у вигляді
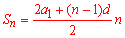
Підставимо у цю формулу заданий запис суми та прирівняємо коефіцієнти при однакових степенях n
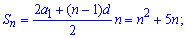
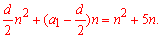
Це і є важлива формула, з якої знаходимо перший член прогресії та різницю (крок)
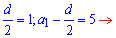
d=2; a1=5+d/2=6.
Обчислюємо 10 член прогресії
a10=a1+9d=6+9*2=24.
Відповідь: a10=24.
Приклад 5. Обчислити суму всіх парних натуральних чисел до 100 включно.
Розв'язання: Перший елемент послідовності рівний a1=2, останній рівний 100. Від 1 до 10 маємо 5 парних чисел. В сотні всього 10 десятків тобто 10*5 парних чисел. Якщо міркувати по іншому, то половина елементів до 100 парні, половина – непарні.
100/2=50 – кількість парних чисел.
Різниця прогресії рівна 2.
Далі підставляємо відомі значення в формулу та обчислюємо
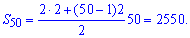
Сума парних чисел до 100 рівна 2550.
Відповідь: S50=2550.
Приклад 6. Обчислити суму всіх двоцифрових натуральних чисел.
Розв'язання: Номер члена прогресії буде рівний його значенню
a1=1;… a99=99.
Різниця прогресії рівна одиниці d=1. Знаходимо суму арифметичної прогресії за формулою
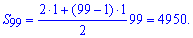
Сума рівна 4950.
Відповідь: S99=4950.
Приклад 7. В арифметичній прогресії а2+a9=9, а8+a4=5. Обчислити різницю прогресії.
Розв'язання: Номер члена прогресії буде рівний його значенню
a1=1;… a99=99.
Різниця прогресії рівна одиниці d=1.
Знаходимо суму арифметичної прогресії за формулою
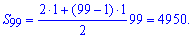
Сума рівна 4950.
Відповідь: S99=4950.
Приклад 8. В арифметичній прогресії а2+a11=10, а5+a6=13. Обчислити різницю прогресії.
Розв'язання: Алгоритм розв'язування подібних прикладів наступний: Виражаємо члени прогресії через один, який має найменший порядковий номер
a11=a2+9d;
a5=a2+3d;
a6=a2+4d.
Підставляємо записи у суми членів прогресії
a2+a2+9d=2*a2+9d=10;
a2+3d+a2+4d=2*a2+7d=13.
Маємо два рівняння з двома невідомими. Для відшукання різниці прогресії від першого рівняння віднімаємо друге
9d-7d=2d=10-13;
2d=-3; d=-1,5.
Відповідь: d=-1,5.
Приклад 9. В арифметичній прогресії а2+a11=10, а5+a6=13. Обчислити a1.
Розв'язання: Завдання аналогічне попередньому. Виражаємо, для зручності, усі члени суми через 1 номер
a2=a1+d; a11=a1+10d;
a5=a1+4d; a6=a1+5d.
Підставляємо у формули і складаємо рівняння
a1+d+a1+10d=2*a1+11d=10;
a1+4d+a1+5d=2*a1+9d=13.
Від першого рівняння віднімемо друге і знайдемо крок прогресії
11d-9d=2d=10-13=-3.
2d=-3; d=-1,5.
Знаючи крок прогресії, перший її елемент знаходимо з рівняння
2*a1+9*(-1,5)=13; 2*a1=13+13,5=26,5;
a1=26,5/2=13,25.
Відповідь: a1=13,25.
Приклад 10. Обчислити суму всіх двоцифрових натуральних чисел, які при діленні на 3 дають в остачі 2.
Розв'язання: Спочатку запишемо загальну формулу члена прогресії для даного завдання. Враховуючи умову матимемо залежність
a[n]=3*n+2.
Перше двоцифрове число, яке задовольняє умову це 11.
a[3]=3*3+2=11.
Останнє число рівне 98 і воно відповідає 32 номеру прогресії
a[32]=3*32+2=98.
Дальше маємо вибір із двох варіантів – шукати часткову суму прогресії або від повної суми відняти перших два елементи. Поступимо за другою схемою
a1=3+2=5; a2=3*2+2=8;
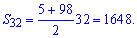
Від знайденої суми віднімаємо перші два елементи прогресії
S=1648-5-8=1635.
Відповідь: S=1635.
Приклад 11. Обчислити суму всіх двоцифрових натуральних чисел, які при діленні на 4 дають в остачі 1.
Розв'язання: Випишемо загальну формулу члена прогресії
a[n]=4*n+1.
Завжди поступайте таким чином для опису прогресії.
Перше потрібне число рівне 13. Його легко отримати перебравши кілька членів прогресії – 5; 9;13; ...
З останнім номером трохи більше пошуків, але також можна встановити, що це буде 97.
a[3]=13; a[24]=97.
Крок прогресії складає d=4.
Знаходимо суму двоцифрових натуральних чисел
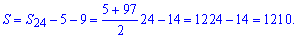
Отримали в сумі 1210.
Відповідь: S=1210.
Приклад 12. Обчислити суму всіх непарних натуральних чисел, від 13до 81 включно.
Розв'язання: Запишемо формулу непарних натуральних чисел.
a[n]=2*n+1, n=0; 1; …
Зробимо заміну в прогресії так, щоб елемент під першим номером дорівнював 13.
a[n]=2*n+1=13.
Звідси n=6. Значить нова прогресія утворюється з попередньої додаванням до індекса n+1=6; n=5.
b[n]=2(n+5)+1.
Знайдемо під яким номером в прогресії іде число 81.
2*(n+5)+1=81;
n+5=(81-1)/2=40; n=35.
Отже b[35]=81.
Знаходимо суму перших 35 членів прогресії
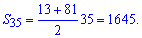
Отже шукана сума дорівнює 1645.
Другий метод полягає у знаходженні суми прогресії a[n] з певного її номера. Для цього потрібно знати формулу, яку деколи немає можливості на контрольній чи тестах виводити з формули суми прогресії
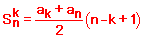
Якщо Ви її знаєте, то в даному випадку потрібну знайти суму від 6 до 40 члена прогресії a[n]
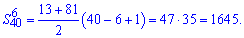
І на "закуску" третій спосіб, який полягає у відніманні від повної суми прогресії суми її перших членів.
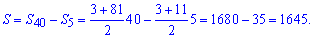
На цьому обчислення прикладу завершені.
Відповідь: S=1645.
Приклад 13. В арифметичній прогресії а18=12,3; a32=2,8. Обчислити а21+a29.
Розв'язання: Якщо Ви уважно переглянули відповіді до попередніх прикладів то знаєте як поступати у цьому завданні. Спершу виражаємо 21 і 29 член прогресії через 18 і 32
a21=a18+(21-18)d=a18+3d;
a29=a32+(29-32)d=a32-3d.
Легко бачити, що при сумуванні різниця прогресії пропадає
a21+a29=a18+a32=12,3+2,8=15,1.
Відповідь: сума рівна 15,1.
Приклад 14. Сума п перших членів арифметичної прогресії виражається формулою Sn=13n2+5n. Обчислити різницю прогресії.
Розв'язання: Подібне завдання розглядали під номером 3, 4. Запишемо загальну формулу суми прогресії та прирівняємо до заданої
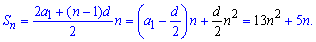
Прирівняємо коефіцієнти при квадраті номера прогресії
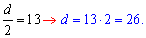
Різниця прогресії рівна 26
Відповідь: d=26.
Приклад 15. Сума п перших членів арифметичної прогресії виражається формулою Sn=3n2+8n. Обчислити різницю прогресії.
Розв'язання: Тут не будемо Вас втомлювати і по аналогії з попереднім прикладом запишемо, що коефіцієнт при квадраті індексу рівний половині різниці прогресії
d/2=3; d=3*2=6.
Як просто знайти різницю прогресії.
Відповідь: d=6.
Приклад 16. У геометричній прогресії bm-n=7,2; bm=9,6. Обчислити bm+n
Розв'язання: На вигляд завдання на геометричну прогресію складне, проте прості формули дозволяють обчислити все.
Запишемо bт через попередній відомий член прогресії bm-n
b[m]=b[m-n]*q^n.
Таке саме виконаємо для bm+n
b[m+n]= b[m]*q^n.
Залишилося з першого рівняння виразити знаменник прогресії
q^n= b[m]/b[m-n]
та підставити у друге
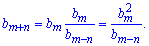
Підставимо задані значення у формулу
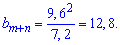
Шуканий член геометричної прогресії рівний 12,8.
Відповідь: b[m+n]=12,8.
Приклад 17. У геометричній прогресії bm+n=6,3; bm=4,2. Обчислити bm-n
Розв'язання: Цей приклад побудований за оберненим принципом до попереднього, хоча хід обчислень подібний. З аналізу значень геометричної прогресії слідує, що bm-n повинно бути меншим від bm=4,2. А з аналогії з попереднім виходить, що відповіддю буде квадрат меншого числа розділений на більше значення.
bm-n= bm* bm/bm+n
і зараз Ви в цьому переконаєтеся.
Запишемо наступні члени геометричної прогресії через попередні
b[m]=b[m-n]*q^n;
b[m+n]= b[m]*q^n.
З першої залежності знаходимо bт-п, а з 2 – q^n.
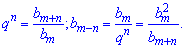
Виконаємо відповідні розрахунки
b[m-n]=4,2*4,2/6,3=2,8.
Відповідь: b[m-n]=2,8.
Приклад 18. В арифметичній прогресії аm+n=1,4; аm-n=92,8. Обчислити аm.
Розв'язання: Невідомий член арифметичної прогресії рівний середньому арифметичному сусідніх елементів. Оскільки аm+n і аm-n є рівновіддаленими елементами прогресії від аm то його знаходимо за формулою
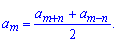
a[m]=(92,8+1,4)/2=47,1.
Відповідь: a[m]=47,1.
Приклад 19. В арифметичній прогресії аm =8,75; аm+n=13,8. Обчислити аm-n.
Розв'язання: Виразимо наступні члени прогресії через попередні
a[m+n]=a[m]+n*d;
a[m]=a[m-n]+ n*d.
З першої формули знаходимо добуток n*d та підставимо у другу
n*d= a[m+n]-a[m];
a[m-n]=a[m]-n*d=2*a[m]-a[m+n].
Підставимо значення у формулу та знайдемо потрібний елемент прогресії
a[m-n]= 2*8,75-13,8=3,7.
Відповідь: a[m-n]=3,7.
Приклад 20. У геометричній прогресії b21*b7=62,7. Обчислити b19 якщо b9=5,5.
Розв'язання: Завдання одне із складних, які розглянуті тут, однак на практиці розв'язати можливо. Запишемо всі старші члени геометричної прогресії через b7
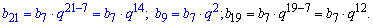
Запишемо добуток 21 і 7 члена геометричної прогресії та розписане b9
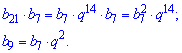
Щоб отримати вираз для 19 члена прогресії потрібно добуток b21*b7 розділити на b9
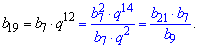
З досвідом Ви побачите, що в подібних прикладах залишається ділити одні значення на другі або множити, приклади де потрібно тягнути корені чи підносити до степені в геометричних прогресіях зустрічаються вкрай рідко.
Обчислюємо b19
b[19]=62,7/5,5=11,4.
Відповідь: b[19]=11,4.
Приклад 21. Обчислити суму перших двадцяти членів арифметичної прогресії (ап), якщо а6 +а9+а12+ а15 = 20 .
Розв'язання: Виглядає на перший погляд незрозуміло, як з такого запису отримати суму. Однак, якщо згадати формулу суми арифметичної прогресії, то все що там фігурує – це перший та останній член суми, а також їх кількість. Таким чином слід представити суму заданих членів прогресії через перший та останній елемент. Запевняю Вас, що різниця прогресії в розрахунках спроститься і задана умова не що інше, як подвоєна сума першого та 20 члена прогресії. В цьому Ви зараз наглядно переконаєтеся. Розписуємо перші два доданки суми через a[1], а останні через a[20].
a[6]=a[1]+5d;
a[9]=a[1]+8d;
a[12]=a[20]-8[d];
a[15]=a[20]-5d.
Просумувавши їх усіх, отримаємо
a[6]+a[9]+a[12]+a[15]=2*a1+2*a[20].
Формула суми 20 членів арифметичної прогресії має вигляд
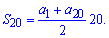
Чисельник дробу і є заданою сумою, розділеною на 2. Тому зразу виконуємо обчислення
S[20]=20/2/2*20=100.
Відповідь: S[20]=100.
Приклад 22. Сума першого і п'ятого членів арифметичної прогресії дорівнює 28, а добуток четвертого і третього членів 280. Обчислити суму перших десяти членів прогресії.
Розв'язання: В цьому завданні і подібних потрібно складати систему рівнянь. Для цього запишемо спершу у мову у вигляді
a[1]+a[5]=28; a[3]*a[4]=28.
Оскільки 3 член прогресії є рівновіддаленим від 1 і 5, то їх середнє арифметичне і буде 3 членом прогресії
a[3]=(a[1]+a[5])/2=28/2=14.
Добуток розпишемо через 3 член прогресії
a[3]*a[4]=a[3]*(a[3]+d)=280;
14*(14+d)=280.
Звідси знаходимо різницю прогресії
14+d=280/14=20;
d=20-14=6.
Обчислимо 1 і 10 член арифметичної прогресії
a[1]=a[3]-2d=14-2*6=2;
a[10]=a[3]+7d=14+7*2=28.
Маємо все необхідне для обчислення суми прогресії
S[10]=(2+28)*10/2=150.
Відповідь: S[10]=150.
Приклад 23. Знайти чотири числа, які утворюють геометричну прогресію, у якій третій член більший за перший на 9, а другий більший за четвертий на 18. У відповіді записати їх суму.
Розв'язання: Запишемо умову завдання у вигляді
b[3]-b[1]=9; b[2]-b[4]=18.
Розпишемо члени геометричної прогресії через 1 елемент
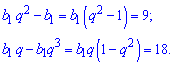
Поділивши перше друге рівняння на перше отримаємо знаменник прогресії
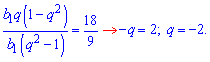
З першого рівняння знаходимо 1 член геометричної прогресії
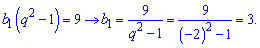
Всі решта члени прогресії отримуємо до множенням попереднього номера на знаменник.
b[2]=b[1]*q=3*(-2)=-6;
b[3]=b[2]*q=-6*(-2)=12;
b[4]=12*(-2)=-24.
Залишилося обчислити суму членів геометричної прогресії
S=3-6+12-24=-15.
Відповідь: S=-15.
Приклад 24. Знаменник геометричної прогресії 1/3, третій член геометричної прогресії 1/9, а сума всіх членів геометричної прогресії 13/9. Знайти кількість членів геометричної прогресії.
Розв'язання: Суму членів геометричної прогресії знаходимо за формулою
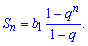
Знайдемо перший член прогресії через 3 та знаменник.
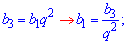
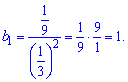
Підставимо значення у формулу суми та знайдемо кількість просумованих членів
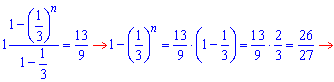
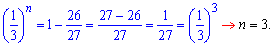
Отже, сумували 3 члени геометричної прогресії.
Відповідь: n=3.
Приклад 25. Дано дві арифметичні прогресії. Перший і п'ятий члени першої прогресії відповідно дорівнюють 7 і -5. Перший член другої прогресії дорівнює 0, а останній 7/2. Обчислити суму членів другої прогресії, якщо відомо, що треті члени обох прогресій рівні між собою.
Розв'язання: Запишемо умову прикладу
a[1]=7;a[5]=-5;
b[1]=0; b[n]=7/2;
a[3]=b[3]; S[n]-?
Знайдемо 3 член першої прогресії через середнє арифметичне сусідніх
a[3]=(a[1]+a[5])/2=(7-5)/2=1.
Враховуючи, що
b[3]=a[3]=1,
знайдемо крок другої прогресії.
b[3]=b[1]+2*d;
1=0+2*d; d=1/2=0,5.
Знайдемо номер останнього члена другої прогресії
b[n]=0+(n-1)d=7/2=3,5;
n-1=3,5/d=3,5/0,5=7;
n=7+1=8.
Знаходимо суму восьми членів прогресії
S[8]=(0+3,5)*8/2=3,5*4=14.
Відповідь: S[8]=14.
Після такої практики, я думаю Ви знаєте як знаходити суму арифметичної та геометричної прогресії. Якщо ні перегляньте приклади від початку (це був жарт).
Якщо приклади були корисні Вам - порекомендуйте їх друзям.
Переглянути схожі матеріали:


