Приклади на арифметичну та геометричну прогресію взято із "Збірника задач для вступників. Математика" виданого Волинським державним університетом імені Лесі Українки у 2001 році. Уважно перегляньте відповіді та виберіть для себе найважливіше.
Група А (рівень 1)
Приклад 1. Обчислити шостий член арифметичної прогресії
21,3; 22,4; …,
Розв'язання: Знайдемо різницю (крок) прогресії
d=a2-a1=22,4-21,3=1,1.
Далі обчислюємо шостий член арифметичної прогресії
a6=a1+(6-1)d=21,3+5*1,1=26,8.
Приклад 2. Обчислити шостий член геометричної прогресії
5; 10; 20; ...
Розв'язання: Знайдемо знаменник геометричної прогресії
q=b2/b1=10/5=2.
Обчислюємо шостий член геометричної прогресії
b6=b1q6-1=5*25=5*32=160.
Він рівний сто шістдесят.
Приклад 3. В арифметичній прогресії a1=2,1 a10=12,9.
Обчислити різницю прогресії.
Розв'язання: Представимо десятий член прогресії у вигляді формули
a10=a1+(10-1)d= a1+9d.
Підставимо відомі значення та розв'яжемо
12,9=2,1+9d;
9d=12,9-2,1=10,8;
d=10,8/9=1,2.
Відповідь: різниця прогресії d=1,2.
Приклад 4. В геометричній прогресії b1=2,56; b4=4,42368.
Обчислити знаменник прогресії.
Розв'язання: Знаходимо знаменник прогресії
q=b2/b1=4,42368/2,56=1,728.
Без калькулятора тут не обійтись.
Відповідь: знаменник прогресії рівний q=1,728.
Приклад 5. В арифметичній прогресії a1=20,1, d=1,3.
Обчислити суму перших восьми членів прогресії.
Розв'язання: Cуму арифметичної прогресії знаходимо за формулою
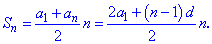Виконуємо обчислення
S8=(2*20,1+(8-1)*1,3)*8/2=197,2.
Відповідь: S8=197,2.
Приклад 6. В геометричній прогресії b1=1,5; q=1,2.
Обчислити суму перших чотирьох членів прогресії.
Розв'язання: Cуму геометричної прогресії обчислюємо за формулою
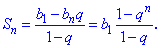
Знаходимо суму прогресії
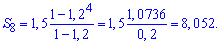
Відповідь: S8=8,052.
Приклад 7. В арифметичній прогресії a1=1,35 d=-2,4.
Обчислити номер члена прогресії, який дорівнює -25,05.
Розв'язання: Член арифметичної прогресії знаходять за формулою
an=a1+(n-1)d.
За умовою задано все крім порядкового номера, знайдемо його
-25,05=1,35+(n-1)(-2,4);
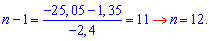
Відповідь: n=12.
Приклад 8. Обчислити сьомий член прогресії
23,5; 24,82; 26,14; ...
Розв'язання: Оскільки в умові не задано, то спершу потрібно встановити, яка прогресія задана. Отримаєте, що арифметична
d=a2-a1=24,82-23,5=1,32;
d=a3-a2=26,14-24,82=1,32.
Знаходимо сьомий член прогресії
a7=a1+(7-1)d=23,5+6*1,32=31,42.
Відповідь: a7= 31,42.
Приклад 9. Обчислити номер члена прогресії 2,1; 3,3; 4,5; ... ,
що дорівнює 11,7.
Розв'язання: Легко переконатись, що задана арифметична прогресія. Знайдемо різницю прогресії
d=a2-a1=3,3-2,1=1,2.
За формулою члена прогресії
an=a1+(n-1)d
знайдемо номер
11,7=2,1+(n-1)*1,2;
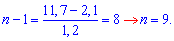
Відповідь: n= 9.
Приклад 10. Обчислити четвертий член прогресії
1,5; 1,8; 2,16; ....
Розв'язання: Без перевірки можна сказати, що прогресія – геометрична. Знайдемо її знаменник
q=b2/b1=1, 8/1,5=1,2.
Обчислимо 4 член геометричної прогресії за формулою
b4=b1q3=1,5*1,23=2,592.
Відповідь: b4=2,592.
Приклад 11. Обчислити номер члена прогресії 1,2; 1,8; 2,16; ... ,
що дорівнює 4,05.
Розв'язання: маємо геометричну прогресію. Знайдемо знаменник прогресії
q=b2/b1=1, 8/1,2=1,5.
Знайдемо номер прогресії із залежності
bn=b1qn-1.
4,05=1,2*1,5n-1;
1,5n-1=4,05/1,2=3,375=1,53;
n-1=3; n=4.
Відповідь: n=4.
Приклад 12. В арифметичній прогресії a5=14,91 a9=20,11.
Обчислити a1.
Розв'язання: Виразимо 9 член прогресії через 5
a9= a5+(9-5)d
та знайдемо крок прогресії
20,11=14,91+4d;
4d=5,2; d=5,2/4=1,3.
Виразимо 5 член прогресії через 1 та обчислимо перший
a5= a1+4d;
14,91= a1+5,2;
a1=14,91-5,2=9,71.
Відповідь: a1=9,71.
Приклад 13. В арифметичній прогресії а7=12,01; a11=17,61.
Обчислити різницю прогресії.
Розв'язання: Виразимо 11 член прогресії через 7
a11= a7+(11-7)d.
Звідси обчислимо крок прогресії
17,61=12,01+4d;
4d=5,6; d=5,6/4=1,4.
Відповідь: d=1,4.
Приклад 14. У геометричній прогресії b5=64; b8=1. Обчислити b3.
Розв'язання: Виразимо 8 член прогресії через 5
b8= b5q8-5.
Звідси знаходимо знаменник прогресії
1=64 q3;
q3=1/64=(1/4)3;
q=1/4.
Відповідно знаходимо b3 через b5
b3= b5/q2=64*42=1024.
Відповідь: b3=1024.
Приклад 15. В арифметичній прогресії а9+а15=14,8.
Обчислити а12
Розв'язання: В цьому прикладі слід врахувати, що 12 член прогресії знаходиться посередині між 9 її номером і 15. Тому сусідні члени прогресії (9, 15) можна виразити через 12 наступним чином
a9= a12-(12-9)d;
a15= a12+(15-9)d;
a9= a12-3d;
a15= a12+3d.
Просумуємо крайні члени прогресії
a9+ a15= a12-3d+ a12+3d=2a12.
Звідси знаходимо 12 член прогресії
a12=(a9+a15)/2=14,8/2=7,4.
Відповідь: a12=7,4.
Приклад 16. В геометричній прогресії b10*b14=289.
Обчислити модуль 12 члена прогресії |b12|.
Розв'язання: Алгоритм розв'язку завдання міститься в попередньому прикладі. Слід виразити 10 і 14 член геометричної прогресії через 12. За властивостями геометричної прогресії отримаємо
b10= b12/q2; b14= b12*q2.
Легко помітити, що при їх добутку знаменник прогресії пропадає
b10* b14= (b12)2=289=172.
Звідси знаходимо модуль| b12|
(b12)2=289=172 -> | b12|=17.
Відповідь: | b12|=17.
Приклад 17. В геометричній прогресії b8=1,3.
Обчислити b6*b10.
Розв'язання: Схема обчислень аналогічна попередньому прикладу – виражаємо 6 і 10 член прогресії через 8.
b6= b8/q2; b10= b8*q2.
При їх множенні знаменники скорочуються і отримаємо квадрат відомого члена прогресії
b6*b10= (b8)2=1,32=1,69.
Відповідь: b6*b10=1,69.
Приклад 18. В арифметичній прогресії а10=3,6: a12=8.
Обчислити а8
Розв'язання: Запишемо члени прогресії в ряд а8, а10, a12. Між ними одинаковий крок, знайдемо його
a12= a10+2d;
2d= a12- a10=8-3,6=4,4.
Таким самим методом знаходимо а8
a10= a8+2d;
a8= a10-2d=3,6-4,4=-0,8.
Ось такі нескладні розрахунки.
Відповідь: a8=-0,8.
Приклад 19. У геометричній прогресії b14=8; b16=2.
Обчислити b12.
Розв'язання: Опускаючи детальні пояснення, запишемо добуток 14 і 16 члена прогресії
b14*b16=(b12)2.
Це рівносильно середньому геометричному. Знайшовши корінь з добутку членів, матимемо шукане значення
(b12)2=8*2=16; b12=4.
Відповідь: b12=4.
Приклад 20. В арифметичній прогресії а5=3,4; a11=6,9.
Обчислити а17.
Розв'язання: Між 5,11 і 17 членом прогресії однаковий крок і він рівний 6d. Тому кінцевий розв'язок можна записати у вигляді
а17= a11+6d= a11+(a11- а5)=2*6,9-3,4=10,4.
Думаю, що Ви розумієте,чому такий запис. Якщо ні – спробуйте розписати 11 член прогресії через 5.
Відповідь: а17=10,4.
Приклад 21. Обчислити 6-й член геометричної прогресії
3; 12;... .
Розв'язання: Знайдемо знаменник прогресії
q=b2/b1=12/3=4.
Скористаємося загальною формулою члена геометричної прогресії
bn= b1*qn-1.
Звідси отримаємо
b6= b1*q5=b2*q4.
Як бачите, головне в записі, щоб сума індексу (2) та степеня (4) відповідала порядковому номеру члена прогресії (6). Виконуємо обчислення
b6= 12*44=12*256=3072.
Отримали велике число, але геометрична прогресія тим і відрізняється, що її члени або швидко зростають, або – спадають.
Відповідь: b6=3072.
Приклад 22. В арифметичній прогресії а3=48; a5=42.
Обчислити а7.
Розв'язання: Оскільки різниця прогресії між заданими членами і шуканим стала і рівна 2d то формула 7 члена прогресії матиме вигляд
а7= a5+2d= a5+(a5- а3);
а7=2*42-48=36.
Відповідь: а7=36.
Приклад 23. Обчислити суму перших п'ятнадцяти непарних чисел.
Розв'язання: Запишемо декілька членів цієї прогресії 1, 3, 5, ... Різниця прогресії рівна d=2. Обчислимо 15 член прогресії
а15= а1+14d=1+14*2=29.
Підставимо у формулу суми арифметичної прогресії
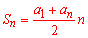
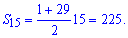
Відповідь: Сума прогресії рівна 225.
Приклад 24. Обчислити перший член арифметичної прогресії, якщо сума перших дванадцяти її членів дорівнює 642 і дванадцятий член дорівнює 48.
Розв'язання: Тут потрібно скласти два рівняння з яких визначити дві невідомі. Суму 12 членів арифметичної прогресії можна знайти за формулою
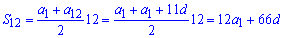
12а1+66d=642.
Друге рівняння запишемо із формули 12 члена прогресії
а12= а1+11d=48.
Виразимо 11d із другого рівняння та підставимо в перше
11d=48-а1;
12а1+6*11d=642;
12а1+6*(48-а1)=642;
6а1+288=642;
6а1=642-288=354;
а1=354/6=59.
Відповідь: а1=59.
Приклад 25. Обчислити знаменник геометричної прогресії, яка складається з дійсних чисел,
якщо b5=162; b8=4374.
Розв'язання: Виразимо 8 член геометричної прогресії через 5
b8= b5*q3.
Звідси виразимо знаменник
q3= b8/ b5=4374/162=27=33; q=3.
Знаменник рівний 3.
Відповідь: q=3.
На цьому прості завдання на арифметичну та геометричну прогресію розв'язано. Добре розберіть наведені варіанти та схеми обчислень, вони не надто складні і зрозуміло обґрунтовані.
Переглянути схожі матеріали:
