Зібрані завдання на арифметичну прогресію містять в умові сторони трикутника, його площу, гіпотенузу. Таких прикладів на прогресії багато, тому ми спробували згрупувати їх за подібністю і типові розжувати Вам. Це допоможе засвоїти методику обчислень і надасть впевненості в подібних завданнях. Крім цього, завдання досить цікаві з практичної сторони, оскільки одночасно поєднують знання геометрії (трикутників) та арифметичної прогресії.
Задача 1. Сторони прямокутного трикутника утворюють арифметичну прогресію. Обчислити площу трикутника, якщо більший катет дорівнює 4.
Розв'язання. Площа прямокутного трикутника рівна половині добутку катетів. Позначимо сторони трикутника a-d, a, a+d.
З наведених позначень площа рівна
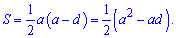
Знайдемо складові формули площі.
Більший катет рівний 4 означає
a =4.
Складаємо рівняння за теоремою Піфагора
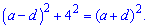
Розкриємо дужки у рівнянні
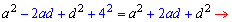
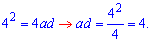
Підставимо знайдене значення у формулу площі
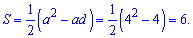
Отже площа рівна 6 квадратних одиниць.
Задача 2. Сторони прямокутного трикутника утворюють арифметичну прогресію. Обчислити периметр трикутника, якщо його гіпотенуза дорівнює 10.
Розв'язання. Знову потрібно знайти певну залежність, з якої визначити сторони. Позначимо відому сторону за а, тоді два катети будуть рівні a-d, a-2d.
Складаємо рівняння гіпотенузи через катети
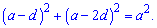
Далі підставляємо значення гіпотенузи та розкриваємо дужки

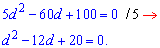
Отримали квадратне рівняння для визначення різниці арифметичної прогресії. Обчислюємо дискримінант
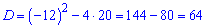
та корені рівняння
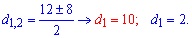
Перше значення відкидаємо, оскільки при d=10 отримаємо не трикутник а пряму. При d=2 сторони трикутника приймуть значення
10;10-2=8; 8-2=6.
Знайдемо периметр трикутника
10+8+6=24.
Ось такі хитрі прийоми часом доводиться застосовувати, щоб отримати правильну відповідь.
Задача 3. Сторони прямокутного трикутника утворюють арифметичну прогресію. Обчислити менший його катет, якщо площа трикутника дорівнює 54.
Розв'язання. З попередніх завдань бачимо, що шуканий трикутник подібний до трикутника зі сторонами 3,4,5, тільки збільшений в декілька разів. Площа найменшого рівна
S=3*4/2=6.
Поділимо 54 на 6, щоб знайти пропорцію між трикутниками
54/6=9.
Отже кожну сторону трикутника треба збільшити на корінь з 9, тобто 3. Шуканий трикутник матиме сторони, 9,12, 15. Менший катет трикутника рівний 9.
Задача 4. Сторони прямокутного трикутника утворюють арифметичну прогресію. Обчислити його периметр, якщо площа трикутника дорівнює 96.
Розв'язання. Методика наступна. Сторони прямокутного трикутника, які рівні 3, 4, 5 утворюють арифметичну прогресію. Площа на їх базі рівна S=6 (з попереднього прикладу). Ділимо задану площу на базову
96/6=16=4*4.
Отже сторони потрібно збільшити у 4 рази, тобто вони рівні
12,16, 20.
Обчислюємо периметр трикутника
P=12+16+20=48.
Задача 5. Сторони прямокутного трикутника утворюють арифметичну прогресію. Обчислити його периметр, якщо медіана, проведена до гіпотенузи, дорівнює 5.
Розв'язання. Завдання і просте і складне одночасно. Суть знаходження розв'язку зводиться до знання однієї теореми, згідно якої для описаного навколо прямокутного трикутника гіпотенуза є діаметром. Відповідно, задана медіана є нічим іншим, як радіус кола. Звідси гіпотенуза рівна двом радіусам, тобто AC=2*5=10, а інші сторони рівні 2*3=6 і 2*4=8.
Знайти периметр трикутника після написаного вище легко
6+8+10=24.
Задача 6. Сторони трикутника, один із кутів якого 120°, утворюють арифметичну прогресію, другий член якої дорівнює 5. Обчислити площу, помножену на корінь з трьох 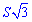 .
.
Розв'язання. Приклад необхідно обчислювати за теоремою косинусів
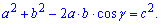
Для початку позначимо сторони через формули прогресії. Найменша 5-d, друга – 5 за умовою, і найбільша 5+d. Підставляємо у рівняння
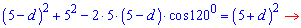
Враховуючи, що cos(120)=-1/2 рівняння спроститься до наступного
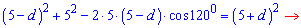
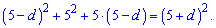
розкриваємо дужки та спрощуємо подібні доданки
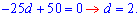
При кроці d=2 менша сторона трикутника рівна 5-2=3. Знаходимо площу трикутника
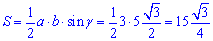
Множимо площу на корінь з трьох
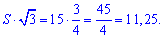
Отримали, що шукана величина рівна 11,25.
Задача 7. У трикутнику з кутом 120 градусів сторони утворюють арифметичну прогресію з різницею 1 см. Знайти периметр.
Розв'язання. Позначимо коротку сторону через х. Тоді середня рівна - (х+1), а довша - (х+2). Найбільша сторона (x+2) лежить навпроти кута 120 градусів. За теоремою косинусів складаємо рівняння (x+2)^2=x^2+(x+1)^2-2*x*(x+1)*cos(120);
(x+2)^2=x^2+(x+1)^2-x*(x+1);
x^2+4x+4=x^2+x^2+2x+1+x^2+x;
2x^2-x-3=0
Дискримінант рівний
D=1+4*3*2=25.
Обчислюємо найменшу сторону
x=(1+5)/4=1,5.
Другий корінь відкидаємо, оскільки він від'ємний x=-1.
Інші сторони відповідно рівні
1,5+1=2,5;
2,5+1=3,5.
Обчислюємо периметр трикутника
P=1,5+2,5+3,5=7,5.
Якщо зустрінете подібні завдання на арифметичну прогресію де в умові задані сторони трикутника, то постарайтеся поділитися з нами. Унікальні приклади будуть добавлені до цієї статті, а можливо оформлені в новій. Все залежить від отриманої кількості завдань та Вашого бажання співпрацювати.
Переглянути схожі матеріали:


