Для полегшення Вам навчання зібрані розв'язки прикладів підвищеної складності з арифметичної та геометричної прогресії. Завдання взяті із "Збірника задач для вступників. Математика" виданого Волинським державним університетом імені Лесі Українки у 2001 році. Методика обчислень є корисною для практичних занять як в школі, так і ВУЗ-ах та відповідає шкільній програмі. Якщо наведені приклади для Вас важкі, прочитайте для початку прості задачі на арифметичну та геометричну прогресію.
Приклад 1. У геометричній прогресії b10* b14* b21=-0,125. Обчислити b15.
Розв'язання. Знайдемо суму індексів членів прогресії.
10+14+21=45.
Число 45 націло ділиться на 15 і в результаті ділення отримуємо 3. Отже заданий добуток не що інше, як
b10* b14* b21=(b15)^3
Звідси обчислюємо потрібний член прогресії
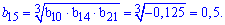
15 член прогресії рівний -0,5.
Приклад 2. Сума трьох чисел, які становлять зростаючу арифметичну прогресію дорівнюють 21. Якщо до них, відповідно, додати 2, 3, і 9, то утворені числа становитимуть геометричну прогресію. Знайти найбільше з шуканих чисел.
Розв'язання. Завдання на знання формул арифметичної та геометричної прогресії. Позначимо члени зростаючої прогресії через a-d, a, a+d. Тоді їх сума рівна 3a=21, звідки a=21/3=7. Отже середній член арифметичної прогресії відомий. Тепер знайдемо члени геометричної прогресії
Перший – a-d+2=7-d+2=9-d
другий a+3=7+3=10.
третій a+d+9=7+d+9=16+d.
За властивістю геометричної прогресії квадрат середнього її члена рівний добутку рівновіддалених, тобто
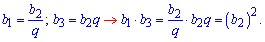
Підставимо члени геометричної прогресії у формулу
(9-d)(16+d)=10^2=100.
Розкриємо дужки та зведемо до квадратного рівняння відносно різниці арифметичної прогресії.
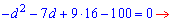
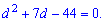
Знаходимо дискримінант
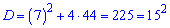
та крок арифметичної прогресії
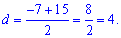
Більший член арифметичної прогресії рівний
a+d=7+4=11.
Ось такі складні завдання на прогресію Вам можуть зустрітися у навчанні.
Приклад 3. Три числа, що становлять зростаючу арифметичну прогресію, дають у сумі 15. Якщо до першого і другого з них додати по одиниці, а до третього числа додати 4, то нові числа становитимуть геометричну прогресію. Знайти найбільше з шуканих чисел.
Розв'язання. Завдання аналогічне попередньому. Вводимо ті самі позначення, тоді середній член арифметичної прогресії рівний 15/3=5, а сусідні – 5-d та 5+d.
Знайдемо члени геометричної прогресії
(5-d+1)=6-d; 5+1=6; 5+d+4=9+d
та складемо з них рівняння
(6-d)(9+d)=6*6=36.
Розкриваємо дужки та зводимо до квадратного рівняння
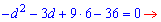
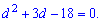
Обчислюємо дискримінант
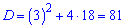
та різницю арифметичної прогресії
d=(-3+9)/2=3.
Найбільше з шуканих чисел рівне 8
a+d=5+3=8.
Приклад 4. Три числа b1, b2, b3 утворюють зростаючу геометричну прогресію. Обчислити b3, якщо b1*b2*b3=64, b1+b2+b3=14.
Розв'язання. Знову маємо завдання на складання рівняння. Позначимо члени геометричної прогресії у вигляді
b/q;b;b*q.
Підставивши в умову можна знайти середній член прогресії
b/q*b*b*q=b^3=64.
Звідси знаходимо середній член геометричної прогресії
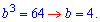
Підставимо значення членів прогресії у другу умову завдання. Враховуючи знайдене значення будемо мати
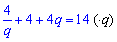
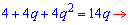

Знаходимо дискримінант рівняння
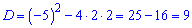
та знаменник геометричної прогресії
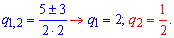
Друге значення відкидаємо, оскільки при ньому геометрична прогресія спадаюча, а за умовою ми шукаємо зростаючу прогресію. Тепер без труднощів знаходимо старший член геометричної прогресії
b*q=4*2=8.
Приклад 5. Три числа b1, b2, b3 утворюють спадну геометричну прогресію. Обчислити b3, якщо b1*b2*b3=27, b1+b2+b3= 13.
Розв'язання. За властивістю геометричної прогресії маємо
b2/q*b2*b2*q=2^3=27.
Звідси b[2]=3. З другої умови отримаємо рівняння
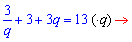
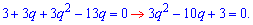
Знаходимо дискримінант квадратного рівняння
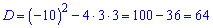
та визначаємо знаменник прогресії
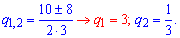
Перше значення q=3 не задовольняє початкову умову. При q=1/3 третій член геометричної прогресії рівний
b[3]=b[2]*q=3/3=1.
Застосовуйте наведений алгоритм обчислень в подібних завданнях.
Приклад 6. Визначити сьомий член зростаючої арифметичної прогресії, якщо а3+а9=24, а3*а9=108.
Розв'язання. Завдання не складне, оскільки маємо дві умови і дві невідомі. Отже розв'язок знайти можна. Виразимо з першого рівняння a[9] та підставимо у друге
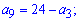
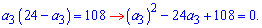
Останнє рівняння розв'язуємо через дискримінант
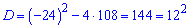
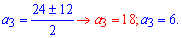
З першої умови
а3+а9=24
бачимо, що при а3=18 прогресія не буде зростаючою. Отже, залишається а3=6. Звідси
a[9]=24-a[3]=24-6=18.
З іншої сторони
a[9]=a[3]+6d
маємо умову для знаходження різниці прогресії
6+6d=18; 6d=12; d=12/6=2.
За формулою знаходимо сьомий член арифметичної прогресії
a[7]=a[3]+4d=6+4*2=14.
Ось і вся схема подібних обчислень.
Приклад 7. Визначити восьмий член зростаючої арифметичної прогресії, якщо а2+а7=18, а2*а7=56.
Розв'язання. Маємо подібне за схемою обчислень завдання. Виразимо з першого рівняння a[2] та підставимо у друге
a[2]=18-a[7]; (18-a[7]) a[7]=56.
Розкриваємо дужки та зводимо до квадратного рівняння
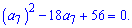
За допомогою дискримінанту
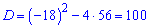
обчислюємо невідомий член прогресії
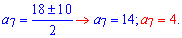
З першої умови робимо висновок, що тільки при a[7]=14 арифметична прогресія буде зростаючою. Відповідно
a[2]=18-a[7]=18-14=4.
За формулою
a[7]=a[2]+5d
визначаємо крок прогресії
14=4+5d; 10=5d; d=2.
Знаходимо 8 член арифметичної прогресії
a[8]=a[7]+d=14+2=16.
Для самоперевірки можете підставити знайдені члени прогресії в умову прикладу.
Приклад 8. Обчислити суму перших восьми членів спадної арифметичної прогресії якщо а2+а6=24, а2*а6=128.
Розв'язання. Щоб знайти суму прогресії нам потрібно знати перший і восьмий член прогресії, або 1 член прогресії і різницю (крок). Для початку визначимо з двох рівнянь хоча би один член прогресії
a[2]=24-a[6];
(24-a[6])*a[6]=128.
При розкритті дужок отримаємо квадратне рівняння
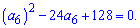
За стандартною схемою порахуємо дискримінант
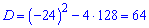
та 6 член арифметичної прогресії
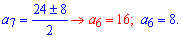
При a[6]=8 арифметична прогресія є спадною. Знаходимо різницю прогресії
a[2]=24-a[6]=24-8=16.
a[6]=a[2]+4d=16+4d=8;
4d=-8;d=-2.
Легко помітити, що значення другого члена прогресії завжди співпадає з коренем рівняння, який відкидаємо за умовою завдання. Це свого роду підказка правильності обчислень. Знаходимо перший і восьмий член прогресії
a[1]=a[2]-d=16-(-2)=18;
a[8]=a[6]+2d=8+2*(-2)=4.
Знайдені значення підставляємо у формулу суми арифметичної прогресії
S=(a[1]+a[8])*8/2=(18+4)*8/2=88.
Сума восьми членів прогресії рівна 88.
Звичайно це не всі приклади, які можна зустріти в інтернеті серед можливих, однак і на їх базі можна витягнути для себе декілька вдалих прийомів, які можна використовувати на практиці при розв'язанні вправ на арифметичну та геометричну прогресії. Вміння приходить з практикою, тому шукайте подібні завдання і самовдосконалюйтесь в обчисленнях!
Переглянути схожі матеріали:


