Арифметическая и геометрическая прогрессия не будет для Вас сложной темой после просмотра следующих примеров. Внимательно ознакомьтесь с ответами среднего уровня сложности и выберите для себя самое необходимое. Если приведенные примеры для Вас тяжелые, прочитайте для начала простые примеры на арифметическую и геометрическую прогрессию (1 уровень).
Группа Б (уровень 2)
Пример 1. В арифметической прогрессии а8=12,4; a23=4,7. Вычислить сумму а14+a17.
Решение: Представим 14 член прогрессии через 8 и 17 через 23. В виде формул они будут запись
a14=а8+6d;
a17=a23-6d.
Находим искомую сумму членов прогрессии
a14+a17=a8+6d+a23-6d=a8+a23;
a14+a17=12,4+4,7=17,1.
Ответ: сумма равна 17,1.
Пример 2. В геометрической профессии b4=3; b17=14,7. Вычислить произведение b9*b12.
Решение: Учитывая свойства геометрической прогрессии, запишем ее 9 член через 4, а 12 через 17.
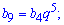
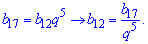
Видим, что при умножении знаменатель геометрической прогрессии упрощается
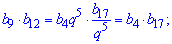
b9*b14=3*14,7=44,1.
Ответ: произведение равно 44,1.
Пример 3. Сумма п первых членов арифметической прогрессии выражается формулой Sn=3n2+6n. Вычислить a6.
Решение: Найдем первый член прогрессии и сумму первых двух
a1=S1=3+6=9;
a1+a2=2a1+d=S2=3*2^2+6*2=24.
Из второго уравнения, учитывая значение первого члена, находим шаг прогрессии
d=24-2a1=24-2*9=6.
По общей формуле вычисляем 6 член арифметической прогрессии
a6=a1+5d=9+5*6=39.
Ответ: a6=39.
Пример 4. Сумма п первых членов арифметической прогрессии выражается формулой Sn=n2+5n. Вычислить a10.
Решение: Задача идентичное предыдущей, только на этот раз попробуем решить по другой методике. Используем сумму арифметической прогрессии в виде
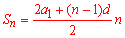
Подставим в эту формулу заданную зависимость суммы и приравняем коэффициенты при одинаковых степенях n
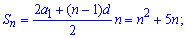
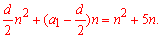
Это и есть важная формула, из которой находим первый член прогрессии и разность (шаг)
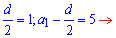
d=2; a1=5+d/2=6.
Вычисляем 10 член прогрессии
a10=a1+9d=6+9*2=24.
Ответ: a10=24.
Пример 5. Вычислить сумму всех четных натуральных чисел до 100 включительно.
Решение: Первый элемент последовательности равен a1=2, последний равен 100. От 1 до 10 имеем 5 четных чисел. В сотни всего 10 десятков то есть 10*5 четных чисел. Если рассуждать по-другому, то половина элементов до 100 четные, половина - нечетные.
100/2=50 – количество четных чисел.
Разница прогрессии равна 2.
Далее подставляем известные значения в формулу и вычисляем
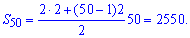
Сумма четных чисел до 100 равна 2550.
Ответ: S50=2550.
Пример 6. Вычислить сумму всех двузначных чисел.
Решение: Номер члена прогрессии будет равен его значению
a1=1;… a99=99.
Разница прогрессии равна единице d=1. Находим сумму арифметической прогрессии по формуле
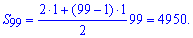
Сумма равна 4950.
Ответ: S99=4950.
Пример 7. В арифметической прогрессии а2+a11=10, а5+a6=13. Вычислить разницу прогрессии.
Решение: Аглоритм решения подобных примеров следующий: Выражаем члены прогрессии через один, имеющий наименьший порядковый номер
a11=a2+9d;
a5=a2+3d;
a6=a2+4d.
Подставляем ету запись в сумму членов прогрессии
a2+a2+9d=2*a2+9d=10;
a2+3d+a2+4d=2*a2+7d=13.
Есть два уравнения с двумя неизвестными. Для отыскания разницы прогрессии от первого уравнения вычитаем второе
9d-7d=2d=10-13;
2d=-3; d=-1,5.
Ответ: d=-1,5.
Пример 8. В арифметической прогрессии а2+a11=10, а5+a6=13. Вычислить a1.
Решение: Задача аналогична предыдущей. Выражаем, для удобства, все члены суммы через 1 номер
a2=a1+d; a11=a1+10d;
a5=a1+4d; a6=a1+5d.
Подставляем в формулы и составляем уравнение
a1+d+a1+10d=2*a1+11d=10;
a1+4d+a1+5d=2*a1+9d=13.
От первого уравнения вычтем второе и найдем шаг прогрессии
11d-9d=2d=10-13=-3.
2d=-3; d=-1,5.
Зная шаг прогрессии, первый ее элемент находим из уравнения
2*a1+9*(-1,5)=13; 2*a1=13+13,5=26,5;
a1=26,5/2=13,25.
Ответ: a1=13,25.
Пример 9. Вычислить сумму всех двузначных натуральных чисел которые при делении на 3 дают в остатка 2.
Решение: Сначала запишем общую формулу члена прогрессии для данной задачи. Учитывая условие получим зависимость
a[n]=3*n+2.
Первое двузначное число, которое удовлетворяет условию это 11.
a[3]=3*3+2=11.
Последнее число равно 98 и оно соответствует 32 номеру прогрессии
a[32]=3*32+2=98.
Дальше есть выбор из двух вариантов - искать частичную сумму прогрессии или от полной суммы вычесть первых два элемента. Поступим по второй схеме
a1=3+2=5; a2=3*2+2=8;
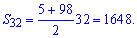
От найденной суммы вычитаем первые два элемента прогрессии
S=1648-5-8=1635.
Ответ: S=1635.
Пример 10. Вычислить сумму всех двузначных натуральных чисел которые при делении на 4 дают в остатка 1.
Решение: Выпишем общую формулу члена прогрессии
a[n]=4*n+1.
Всегда поступайте таким образом для описания прогрессии.
Первое нужное число равно 13. Его легко получить взяв несколько членов прогрессии – 5; 9;13; ...
С последним номером немного больше поисков, но можно установить, что это будет 97.
a[3]=13; a[24]=97.
Шаг прогрессии составляет d=4.
Находим сумму двузначных натуральных чисел
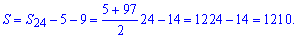
Получили в сумме 1210.
Ответ: S=1210.
Пример 11. Вычислить сумму всех нечетных натуральных чисел от 13до 81 включительно.
Решение: Запишем формулу нечетных чисел.
a[n]=2*n+1, n=0; 1; …
Сделаем замену в прогрессии так, чтобы элемент под первым номером был равен 13.
a[n]=2*n+1=13.
Отсюда n=6. Значит новая прогрессия выходит с предыдущей добавлением к индексу n+1=6; n=5.
b[n]=2(n+5)+1.
Найдем под каким номером в прогрессии идет число 81.
2*(n+5)+1=81;
n+5=(81-1)/2=40; n=35.
Итак b[35]=81.
Находим сумму первых 35 членов прогрессии
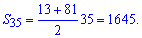
Следовательно, искомая сумма равна 1645.
Второй метод заключается в нахождении суммы прогрессии a[n] с определенного ее номера. Для этого нужно знать формулу, которую порой нет возможности на контрольных или тестах выводить из формулы суммы прогрессии
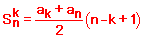
Если Вы ее знаете, то в этом случае нужную найти сумму от 6 до 40 члена прогрессии a[n]
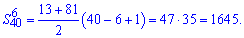
И на "закуску" третий способ, который заключается в вычитании из полной суммы прогрессии суммы ее первых членов.
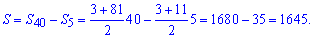
На этом вычисления примера завершены.
Ответ: S=1645.
Пример 12. В арифметической прогрессии а18=12,3; a32=2,8. Вычислить а21+a29.
Решение: Если Вы внимательно просмотрели ответы в предыдущих примерах то знаете как поступить в этом задании. Сначала выражаем 21 и 29 член прогрессии через 18 и 32.
a21=a18+(21-18)d=a18+3d;
a29=a32+(29-32)d=a32-3d.
Легко видеть, что при суммировании разница прогрессии пропадает
a21+a29=a18+a32=12,3+2,8=15,1.
Ответ: сумма равна 15,1.
Пример 13. Сумма п первых членов арифметической прогрессии выражается формулой Sn=13n2+5n. Вычислить разницу прогрессии.
Решение: Подобная задача рассматривали под номером 3, 4. Запишем общую формулу суммы прогрессии и приравняем к заданной
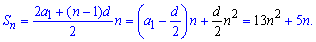
Приравняем коэффициенты при квадрате номера прогрессии
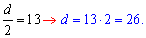
Разница прогрессии равна 26
Ответ: d=26.
Пример 14 Сумма п первых членов арифметической прогрессии выражается формулой Sn=3n2+8n. Вычислить разницу прогрессии.
Решение: Здесь не будем Вас утомлять и по аналогии с предыдущим примером запишем, что коэффициент при квадрате индекса равен половине разницы прогрессии
d/2=3; d=3*2=6.
Видим, наскоько просто найти разницу прогрессии.
Ответ: d=6.
Пример 15. В геометрической прогрессии bm-n=7,2; bm=9,6. Вычислить bm+n
Решение: На вид задания на геометрическую прогрессию сложное. Однак простые формулы позволяют вычислить все.
Запишем bm через предварительный известный член прогрессии bm-n
b[m]=b[m-n]*q^n.
Такое же выполним для bm+n
b[m+n]= b[m]*q^n.
Осталось из первого уравнения выразить знаменатель прогрессии
q^n= b[m]/b[m-n]
и подставить во второе
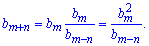
Подставим заданные значения в формулу
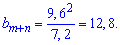
Искомый член геометрической прогрессии равен 12,8.
Ответ: b[m+n]=12,8.
Пример 16. В геометрической прогрессии bm+n=6,3; bm=4,2. Вычислить bm-n
Решение: Этот пример построен по обратному принципом к предыдущему, однако ход вычислений подобный. Из анализа значений геометрической прогрессии следует, что bm-n должен быть меньше bm=4,2. А аналогии с предыдущим примером позволяют припустить, что ответом будет квадрат меньшего числа разделен на большее значение.
bm-n= bm* bm/bm+n
и сейчас Вы в этом убедитесь.
Запишем следующие члены геометрической прогрессии через предыдущие
b[m]=b[m-n]*q^n;
b[m+n]= b[m]*q^n.
С первой зависимости находим bт-п, а з 2 – q^n.
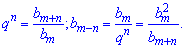
Выполним соответствующие расчеты
b[m-n]=4,2*4,2/6,3=2,8.
Ответ: b[m-n]=2,8.
Пример 17. В арифметической прогрессии ат+п=1,4; ат-п=92,8. Вычислить ат.
Решение: Неизвестный член арифметической прогрессии равен среднему арифметическому соседних элементов. Поскольку ат+п и ат-п есть равноудалены елементами прогрессии от ат , то его находим по формуле
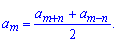
a[m]=(92,8+1,4)/2=47,1.
Ответ a[m]=47,1.
Пример 18. В арифметической прогрессии ат =8,75; ат+п=13,8. Вычислить a[m-n]
Решение: Выразим следующие члены прогрессии через предыдущие
a[m+n]=a[m]+n*d;
a[m]=a[m-n]+ n*d.
С первой формулы находим произведение n*d и подставляем во вторую
n*d= a[m+n]-a[m];
a[m-n]=a[m]-n*d=2*a[m]-a[m+n].
Подставим значение в формулу и найдем нужный элемент прогрессии
a[m-n]= 2*8,75-13,8=3,7.
Ответ: a[m-n]=3,7.
Пример 19. В геометрической прогрессии b21*b7=62,7. Вычислить b19 если b9=5,5.
Решение: Задача одна из сложных среди всех которые рассмотренные здесь, однако на практике решить возможно. Запишем все старшие члены геометрической прогрессии через b7
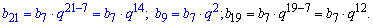
Запишем произведение 21 и 7 члена геометрической прогрессии и расписано b9
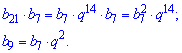
Чтобы получить выражение для 19 члена прогрессии нужно произведение b21*b7 разделить на b9
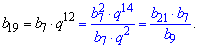
С опытом Вы увидите, что в подобных примерах остается делить одни значения на вторые или умножать, примеры где нужно тянуть корни или подносить к степени в геометрических прогрессиях встречаются крайне редко.
Вычисляем b19
b[19]=62,7/5,5=11,4.
Ответ: b[19]=11,4.
Пример 20. Вычислить сумму первых двадцати членов арифметической прогрессии (аn) если а6 +а9+а12+ а15 = 20 .
Решение: Выглядит на первый взгляд непонятно, как с такой записи получить сумму. Однако, если вспомнить формулу суммы арифметической прогрессии, то все что там фигурирует - это первый и последний член суммы, а также их количество. Таким образом следует представить сумму заданных членов прогрессии через первый и последний элемент. Уверяю Вас, что разница прогрессии в расчетах упростится и заданное условие не что иное, как удвоенная сумма первого и 20 члена прогрессии. В этом Вы сейчас наглядно убедитесь. Расписываем первые два слагаемые суммы через a [1], а остальные через a[20].
a[6]=a[1]+5d;
a[9]=a[1]+8d;
a[12]=a[20]-8[d];
a[15]=a[20]-5d.
Просуммировав их всех получим
a[6]+a[9]+a[12]+a[15]=2*a1+2*a[20].
Формула суммы 20 членов арифметической прогрессии имеет вид
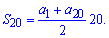
Числитель дроби и является заданной суммой, разделенной на 2 Поэтому сразу выполняем вычисления
S[20]=20/2/2*20=100.
Ответ: S[20]=100.
Пример 21. Сумма первого и пятого членов арифметической прогрессии равна 28,а произведение четвертого и третьего членов 280. Вычислить сумму первых десяти членов прогрессии.
Решение: В этом задании и подобных нужно составлять систему уравнений. Для этого запишем сначала условие задания в виде
a[1]+a[5]=28; a[3]*a[4]=28.
Поскольку 3 член прогрессии является равноудален от 1 и 5, то их среднее арифметическое и будет 3 членом прогрессии
a[3]=(a[1]+a[5])/2=28/2=14.
Произведение распишем через 3 член прогрессии
a[3]*a[4]=a[3]*(a[3]+d)=280;
14*(14+d)=280.
Отсюда находим разницу прогрессии
14+d=280/14=20;
d=20-14=6.
Вычислим 1 и 10 член арифметической прогрессии
a[1]=a[3]-2d=14-2*6=2;
a[10]=a[3]+7d=14+7*2=28.
Есть все необходимые елементы для вычисления суммы прогрессии
S[10]=(2+28)*10/2=150.
Ответ: S[10]=150.
Пример 22. Знайты четыре числа которые образуют геометрическую прогрессию в которой третий член больше первого на 9, а второй больше четвертого на 18. В ответе записать их сумму.
Решение: Запишем условие задачи в виде
b[3]-b[1]=9; b[2]-b[4]=18.
Распишем члены геометрической прогрессии через 1 элемент
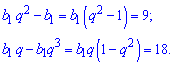
Поделив второе уравнения на первое получим знаменатель прогрессии
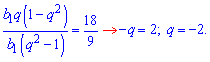
Из первого уравнения находим 1 член геометрической прогрессии
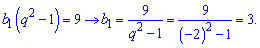
Все остальные члены прогрессии получаем умножением предыдущего номера на знаменатель.
b[2]=b[1]*q=3*(-2)=-6;
b[3]=b[2]*q=-6*(-2)=12;
b[4]=12*(-2)=-24.
Осталось вычислить сумму членов геометрической прогрессии
S=3-6+12-24=-15.
Ответ: S=-15.
Пример 23. Знаменатель геометрической прогрессии 1/3, третий член геометрической прогрессии 1/9, а сумма всех членов геометрической прогрессии 13/9. Найти количество членов геометрической прогрессии.
Решение: Сумма членов геометрической прогрессии находим по формуле
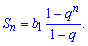
Найдем первый член прогрессии через 3 и знаменатель.
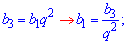
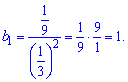
Подставим значение в формулу суммы и найдем количество суммируемых членов
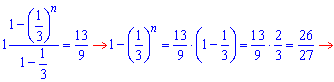
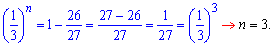
Итак, получили 3 члена геометрической прогрессии.
Ответ: n=3.
Пример 24. Дано две арифметические прогрессии. Первый и пятый члены первой прогрессии соответственно равны 7 и -5. Первый член второй прогрессии равна 0, а последний 7/2. Вычислить сумму членов второй прогрессии если известно,что третьи члены обеих прогрессий равны между собой.
Решение: Запишем условие примера
a[1]=7;a[5]=-5;
b[1]=0; b[n]=7/2;
a[3]=b[3]; S[n]-?
Найдем 3 член первой прогрессии через среднее арифметическое соседних
a[3]=(a[1]+a[5])/2=(7-5)/2=1.
Учитывая что
b[3]=a[3]=1,
найдем шаг второй прогрессии.
b[3]=b[1]+2*d;
1=0+2*d; d=1/2=0,5.
Найдем номер последнего члена второй прогрессии
b[n]=0+(n-1)d=7/2=3,5;
n-1=3,5/d=3,5/0,5=7;
n=7+1=8.
Вычислим сумму восьми членов прогрессии
S[8]=(0+3,5)*8/2=3,5*4=14.
Ответ: S[8]=14.
После такой практиктики я думаю Вы знаете как находить сумму арифметической и геометрической прогрессии. Если нет ознакомьтесь с примерами изначально (это была шутка).
Похожие материалы:
Если примеры были полезны Вам - посоветуйте их друзьям.

