Прогресії середньої складності наведені на поширених для школи та вступу прикладах і стануть в нагоді всім хто їх уважно розбере, а також візьме для себе нове та потрібне. Методика обчислень не нова і не унікальна, однак хто прогресії не використовує часто - довго розжовує наведені приклади і, можливо, не може порахувати.
Приклад 1. В арифметичній прогресії а3+а9+а11+а13=48.
Обчислити а9
Розв'язання. В цьому та подібних завданнях необхідно записати суму арифметичної прогресії через один із її членів. Який саме? – підказує завдання, тому розписуємо усі члени прогресії через 9 та підставляємо у формулу суми
a9-6d+a9+a9-2d+a9-4d=4*a9;
4*a9=48; a9=48/4=12.
Таким чином знайшли 9 член прогресії і він рівний 12.
Приклад 2. У геометричній прогресії b3* b9* b11* b13=625.
Обчислити |b9|
Розв'язання. Даний приклад обчислюємо за тим же алгоритмом, тільки слід пам'ятати, що маємо справу з геометричною прогресією. Виписуємо формули членів геометричної прогресії, що фігурують в добутку, через 9
b3=b9/q6; b11=b9*q2; b13=b9*q4
та підставляємо у формулу
b9/q6*b9*b9*q2*b9*q4=(b9)4;
(b9)4=625. Не важко знайти додатний корінь четвертого степеня з 625, він рівний 5. Отже 9 член прогресії рівний 5
|b9|=5.
Приклад 3. В арифметичній прогресії а11=13,5.
Обчислити а5+а11+а12+а16.
Розв'язання. Запишемо потрібні члени прогресії через 11. Не важко здогадатися, що крок арифметичної прогресії має скоротитися при сумуванні
a5=a11-6d; a12=a11+d; a16=a11+5d.
Уважно перегляньте наведені записи, при їх підстановці в умову отримаємо
а5+а11+а12+а16=4* a11=4*13,5=54.
Сума членів прогресії рівна 54.
Приклад 4. У геометричній прогресії b11=4.
Обчислити b5* b11* b12* b16.
Розв'язання. Тут розжовувати знайомі Вам формули не будемо. Наведемо лиш перевірочну схему. Обчислимо суму індексів членів прогресії у добутку
5+11+12+16=44.
Дане число (44) ділиться без остачі на 11 і у відповіді отримаємо 4. Отже добуток b5* b11* b12* b16 рівний добутку 4 b11 або(b11) 4.
b5* b11* b12* b16 =(b11) 4=44=256.
Приклад 5. В арифметичній прогресії а4n=18, а2n=12.
Обчислити аn
Розв'язання. Необхідно певним чином виразити відомі члени прогресії через той, який потрібно знайти. Запишемо спочатку формулами
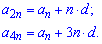
В рівняннях фігурує різниця прогресії (d), щоб її позбутися від 1 рівняння помноженого на 3 віднімемо друге
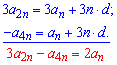
З цієї залежності записуємо формулу для обчислення
a[n] a[n]=(3a[2n]-a[4n])/2.
Підставляємо значення членів прогресії та обчислюємо
a[n]=(3*12-18)/2=9.
Приклад 6. У геометричній прогресії з додатним знаменником b4n=4, b2n=25.
Обчислити bn
Розв'язання. Запишемо відомі члени геометричної прогресії через невідомий
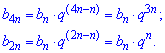
Розділимо перше рівняння на друге, в результаті знайдемо знаменник геометричної прогресії
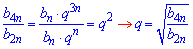
Обчислимо його значення
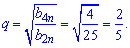
З другого рівняння виразимо потрібний член прогресії
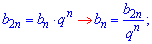
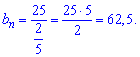
Отже b[n]=62,5, а Ви тепер знаєте, як знайти член геометричної прогресії в подібних завданнях.
Приклад 7. В арифметичній прогресії а[n]=9, а[2n] = 12.
Обчислити а[4n].
Розв'язання. Запишемо молодші члени прогресії через старший
a[n]=a[4n]-3n*d;
a[2n]=a[4n]-2n*d.
Далі є 2 способи знайти член арифметичної прогресії.
Перший – виключенням з рівнянь кроку прогресії;
Другий – знаходженням кроку.
В даному завданні друга схема простіша. Від другого рівняння віднімемо перше, в результаті матимемо
a[2n]-a[n]=n*d.
Обчислимо різницю прогресії
n*d=12-9=3
та підставимо у другу формулу
a[4n]=a[2n]+2n*d=12+2*3=18.
Ось і всі обчислення.
Знайдіть в інтернеті чи збірниках аналогічні завдання та спробуйте перевірити знання самостійно. Це допоможе краще засвоїти методику і перевірити знання властивостей арифметичної та геометричної прогресій.
Переглянути схожі матеріали:


