Арифметичною прогресією називають послідовність чисел (членів прогресії)

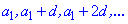
в якій кожен наступний член відрізняється від попереднього на сталий доданок, який ще називають кроком або різницею прогресії.

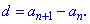
Таким чином, задаючи крок прогресії та її перший член можна знайти будь-який її елемент за формулою

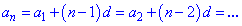
Властивості арифметичної прогресії

1) Кожен член арифметичної прогресії, починаючи з другого номера є середнім арифметичним від попереднього та наступного члена прогресії

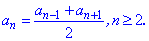
Обернене твердження також вірне. Якщо середнє арифметичне сусідніх непарних (парних) членів прогресії рівне члену, який стоїть між ними то дана послідовність чисел є арифметичною прогресією. За цим твердженням дуже просто перевірити будь-яку послідовність.

Також за властивістю арифметичної прогресії, наведену вище формулу можна узагальнити до наступної

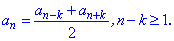
В цьому легко переконатися, якщо розписати доданки справа від знака рівності

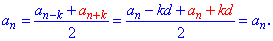
Її часто застосовують на практиці для спрощення обчислень в задачах.

2) Суму n перших членів арифметичної прогресії обчислюють за формулою

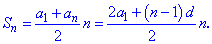
Запам'ятайте добре формулу суми арифметичної прогресії, вона незамінна при обчисленнях та досить часто зустрічається в простих життєвих ситуаціях.

3) Якщо потрібно знайти не всю суму, а частину послідовності починаючи з k-го її члена то в нагоді Вам стане наступна формула суми

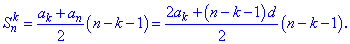
4) Практичний інтерес має відшукання суми n членів арифметичної прогресії починаючи з k-го номера. Для суми використовуйте формулу

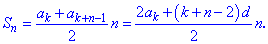
На цьому теоретичний матеріал добігає кінця і переходимо до розв'язування поширених на практиці задач на прогресію.

Приклад 1. Знайти сороковий член арифметичної прогресії 4; 7; ...

Розв'язання: Згідно умови маємо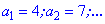
Визначимо крок прогресії

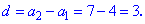
За відомою формулою знаходимо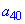

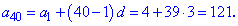
На цьому обчислення закінчено.

Приклад 2. Арифметична прогресія задана третім та сьомим її членом 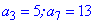. Знайти перший член прогресії та суму десяти.

Розв'язання:Розпишемо задані елементи прогресії за формулами

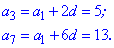
Від другого рівняння віднімемо перше, в результаті знайдемо крок прогресії

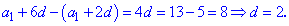
Знайдене значення підставляємо в любе із рівнянь для відшукання першого члена арифметичної прогресії

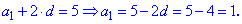
Обчислюємо суму перших десяти членів прогресії

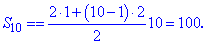
Всі шукані величини знайдені.

Приклад 3. Арифметичну прогресію задано знаменником d=5 та одним з її членів 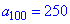. Знайти перший член прогресії , суму 50 її членів починаючи з 50 та суму 100 перших.

Розв'язання:Запишемо формулу сотого елемента прогресії у вигляді

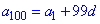
Можемо знайти перший член прогресії

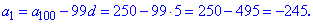
На основі першого знаходимо 50 член прогресії

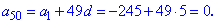
Знаходимо часткову суму прогресії

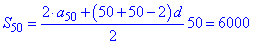
та суму перших 100 членів

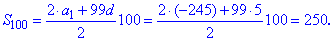
Якщо попередньої формули не знати, то її результат можна отримати віднявши від суми ста членів прогресії суму 49.
Догадайтесь, чому так?

Приклад 4. Знайти число членів арифметичної прогресії, якщо:
а3-а1=8, а2+а4=14, Sn=111.

Розв'язання:Запишемо рівняння через перший член та крок прогресії та визначимо їх

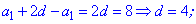
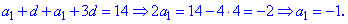
Отримані значення підставляємо у формулу суми для визначення кількості членів у сумі

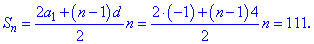
Виконуємо спрощення формули

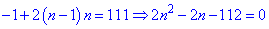
та розв'язуємо квадратне рівняння

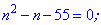
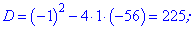
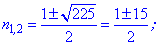
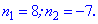
Із знайдених двох значень умові задачі підходить лише число 8. Таким чином, сума перших восьми членів прогресії рівна 111.

Приклад 5. Розв'язати рівняння
1+3+5+...+х=307.

Розв'язання: Дане рівняння є сумою арифметичної прогресії. Випишемо перший її член та знайдемо різницю прогресії

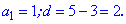
Знайдені величини підставимо в формулу суми прогресії для відшукання кількості доданків

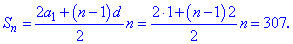
Як і в попередньому завданні, виконуємо спрощення та розв'яжемо квадратне рівняння

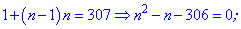
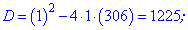
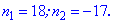
Вибираємо більше із двох значень. Маємо, що сума 18 членів прогресії з заданими величинами а1=1, d=2 рівна Sn=307.
На цьому знайомство із арифметичними прогресіями завершується. В книжках ви знайдете багато подібних задач та нових, які не були розглянуті. Наведеного матеріалу повинно вистачити Вам з головою, щоб розібратися і розв'язати задачі самостійно. Якщо ж ні то звертайтеся і ми Вам допоможемо з обчисленнями.