Практикум з ТІМС
Обчислення моди, медіани, дисперсії, середнього квадратичного відхилення, коефієнта асиметрії та ексцесу
Завдання 1. Побудувати статистичний розподіл вибірки, записати емпіричну функцію розподілу та обчислити такі числові характеристики:
- вибіркове середнє;
- вибіркову дисперсію;
- підправлену дисперсію;
- вибіркове середнє квадратичне відхилення;
- підправлене середнє квадратичне відхилення;
- розмах вибірки;
- медіану;
- моду;
- квантильне відхилення;
- коефіцієнт варіації;
- коефіцієнт асиметрії ;
- ексцес для вибірки:
Вибірка задана наступними значеннями
4, 9, 7, 4, 7, 5, 6, 3, 4, 5, 7, 2, 3, 8, 5, 6, 7, 4, 3, 4.
Розв'язання: Записуємо вибірку у вигляді варіаційного ряду (у порядку зростання):
2; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 7; 7; 7; 7; 8; 9.
Запишемо статистичний розподіл вибірки у вигляді дискретного статистичного розподілу частот:
![]()
Значення емпіричної функції розподілу визначаємо за формулою
![]()
де nx кількість елементів вибірки, що менші за х. Використовуючи таблицю, а також враховуючи, що обсяг вибірки n=1+3+5+3+2+4+1+1=20, запишемо емпіричну функцію розподілу:
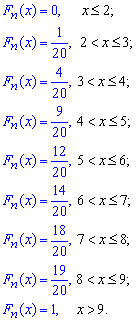
Далі обчислимо числові характеристики статистичного розподілу вибірки.
1. Вибіркове середнє обчислюємо за формулою
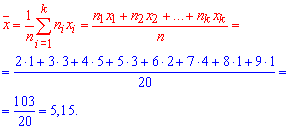
2. Вибіркову дисперсію обчислюємо за формулою
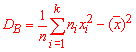
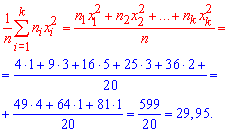
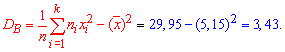
3. Підправлену дисперсію встановлюємо за формулою
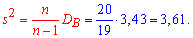
4. Вибіркове середнє квадратичне відхилення обчислюємо за формулою
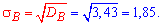
5. Підправлене середнє квадратичне відхилення знаходимо за формулою
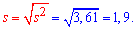
6. Розмах вибірки обчислюємо як різницю між найбільшим і найменшим значеннями її варіант, тобто:
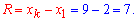
7. Медіану визначають за формулами:
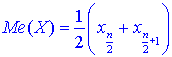 якщо число n – парне;
якщо число n – парне;
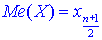 якщо число n – непарне.
якщо число n – непарне.
Тут беремо індекси в x[i] згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку п=20, тому
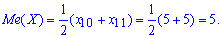
8. Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
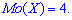
9. Квантильне відхилення знайдемо за формулою
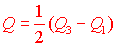
половини різниці 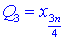 – третього та
– третього та 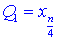 – першого квантилів.
– першого квантилів.
Самі ж квантилі отримуємо штучним розбиттям варіаційного ряду на 4 однакові частини. У нашому випадку
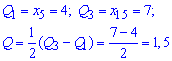
10. Коефіцієнт варіації обчислюємо за формулою
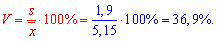
11. Коефіцієнт асиметрії знаходимо за формулою
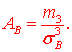
Тут m3 центральний емпіричний момент 3-го порядку,
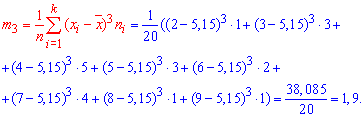
Звідси коефіцієнт асиметрії рівний 0,3
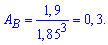
12. Ексцесом EB статистичного розподілу вибірки називається число, яке знаходять за формулою:
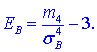
В чисельнику маємо m4 центральний емпіричний момент 4-го порядку,
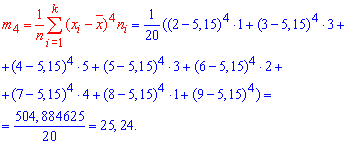
Момент та середня квадратичне відхилення підставляємо у формулу та визначаємо ексцес
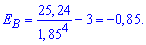
ПРАКТИКУМ з теорії ймовірностей і математичної статистики
Завдання 4.1 За даними вибірки знайти моду та медіану.
|
xi |
1 |
3 |
4 |
5 |
8 |
9 |
|
ni |
30 |
19 |
10 |
16 |
15 |
10 |
Розв'язування: Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
M0(X)=1,
(адже при найбільшій частоті n=30 маємо x30=1).
Формули медіани для дискретного закону розподілу мають вигляд:
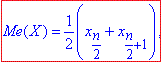 якщо число n= ∑ni – парне,
якщо число n= ∑ni – парне,
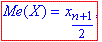 якщо число n – непарне,
якщо число n – непарне,
тут беремо індекси в xi згідно з нумерацією варіант у варіаційному ряді, у нашому випадку n=∑ni=100, (при n=50 маємо x50=4 і при n=51 маємо x51=4), тому
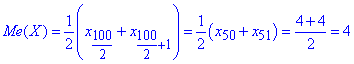
Відповідь: M0(X)=1, Me(X)=4.
Завдання 4.2 За даними вибірки знайти середнє вибіркове 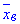 .
.
|
xi |
1 |
3 |
4 |
5 |
8 |
9 |
|
ni |
30 |
19 |
10 |
16 |
15 |
10 |
Розв'язування: Вибіркове середнє x знаходимо за формулою
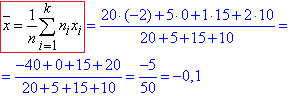
Відповідь: x=-0,1.
З того, як все доступно і зрозуміло на практиці виглядає робимо висновок, що знайти моду, медіану та дисперсію повинен вміти кожен, хто вивчає ймовірність.
]]>Знаходження числових характеристик статистичного розподілу
Варіант 13 . Індивідуальне завдання 1.
Завдання 1. Побудувати статистичний розподіл вибірки, записати емпіричну функцію розподілу та обчислити такі числові характеристики:
- вибіркове середнє;
- вибіркову дисперсію;
- підправлену дисперсію;
- вибіркове середнє квадратичне відхилення;
- підправлене середнє квадратичне відхилення;
- розмах вибірки;
- медіану;
- моду;
- квантильне відхилення;
- коефіцієнт варіації;
- коефіцієнт асиметрії ;
- ексцес для вибірки:
Завдання сформовані у вигляді таблиці (далі – по варіантах, № варіанту = № студента у списку групи)
7, 6, 5, 8, 6, 5, 6, 9, 8, 7, 10, 5, 4, 9, 7, 9, 6, 9, 11, 6.
Розв'язання:
Запишемо вибірку у вигляді варіаційного ряду (у порядку зростання):
4; 5; 5; 5; 6; 6; 6; 6; 6; 7; 7; 7; 8; 8; 9; 9; 9; 9; 10; 11.
Запишемо статистичний розподіл вибірки у вигляді дискретного статистичного розподілу частот:
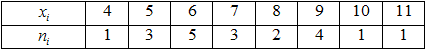 Емпіричну функцію розподілу визначатимемо за формулою
Емпіричну функцію розподілу визначатимемо за формулою
![]()
де nx кількість елементів вибірки, що менші за х.
Використовуючи таблицю і враховуючи, що обсяг вибірки
![]()
запишемо емпіричну функцію розподілу:
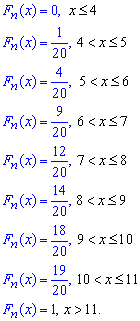

Далі обчислимо числові характеристики статистичного розподілу вибірки.
1) Вибіркове середнє знайдемо за формулою
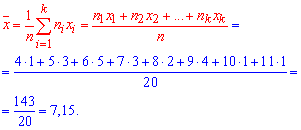
2) Вибіркову дисперсію обчислюємо за формулою
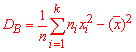
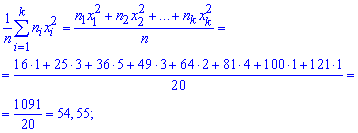
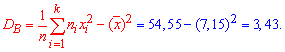
3) Підправлену дисперсію знаходимо за формулою
![]()
4) Вибіркове середнє квадратичне відхилення обчислюємо за формулою
![]()
5) Підправлене середнє квадратичне відхилення знаходимо з формули
![]()
6) Розмах вибірки визначаємо як різницю між найбільшим і найменшим значеннями її варіантів, тобто:
![]()
7) Медіану обчислюють за формулами:
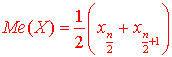
якщо число n – парне;
![]()
якщо число п – непарне.
Тут беремо індекси в ![]() згідно з нумерацією варіант у варіаційному ряді.
згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку п=20, тому
![]()
8) Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто Mo(X)=6.
9) Квантильне відхилення обчислюють за формулою
![]()
де ![]() – перший квантиль,
– перший квантиль, ![]() – третій квантиль.
– третій квантиль.
Квантилі отримуємо, якщо варіаційний ряд розбити на 4 однакові частини.
У нашому випадку
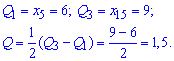

10) Коефіцієнт варіації встановимо із залежності
![]()
11) Обчислюємо коефіцієнт асиметрії
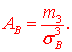
Тут ![]() центральний емпіричний момент 3-го порядку,
центральний емпіричний момент 3-го порядку,
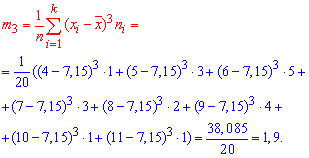
Отже, коефіцієнт асиметрії рівний 0,3
![]()
12) Ексцесом EB статистичного розподілу вибірки називається число, яке знаходять за формулою:
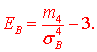
Тут m4 центральний емпіричний момент 4-го порядку,
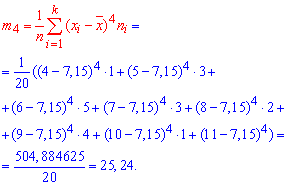
Отже, отримаємо від'ємний ексцес
На цьому індивідуальне завдання №1 розв'язано. З нього Ви повинні навчитися знаходити числові характеристики дискретного розподілу.
Завдання 1.Куб, всі грані якого замальовані, розпиляний на 1000 кубиків однакового розміру. Визначити ймовірність того, що кубик, витягнутий навмання, матиме :
- а) одну замальовану грань;
- б) дві замальовані грані.
Обчислення: Якщо куб розпиляти на кубики однакового розміру, то всі грані будуть поділені на 100 квадратів. (Приблизно як на малюнку)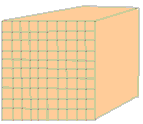 Далі за умовою кубик повинен мати одну замальовану грань – це означає, що кубики повинні належати зовнішній поверхні, але не лежати на ребрах куба (2 замальовані поверхні) і не на кутах – мають три поверхні.
Далі за умовою кубик повинен мати одну замальовану грань – це означає, що кубики повинні належати зовнішній поверхні, але не лежати на ребрах куба (2 замальовані поверхні) і не на кутах – мають три поверхні.
Отже шукана кількість рівна добутку 6 граней на кількість кубиків в квадраті розміром 8*8.
6*8*8=384 – кубики з 1 замальованою поверхнею.
Ймовірність рівна кількості сприятливих подій до загальної їх кількості P=384/1000=0,384.
б) Дві замальовані грані мають кубики по ребрах без вершин куба. На одному ребрі буде 8 таких кубиків. Всього в кубі 12 ребер, тому дві замальовані грані матимуть
8*12=96 кубиків.
А ймовірність витягнути їх серед 1000 всіх рівна
P=96/1000=0,096.
Завдання 2. На однакових картках написані букви А, А, А, Н, Н, С. Яка ймовірність того, що випадково розмістивши картки в ряд, отримаємо слово АНАНАС?
Обчислення: Потрібно розмірковувати завжди від того, що відомо. Дано 3 букви А, 2-Н,та 1 – С, всього їх 6. Почнемо вибирати букви для слова "ананас". Першою йде буква А, її можемо вибрати 3 способами із 6, бо є 3 букви А серед 6 відомих. Тому ймовірність витягнути першою А рівна
P1=3/6=1/2.
Друга буква Н, але слід не забувати, що після того як витягнули А залишається 5 букв для вибору. Тому ймовірність витягнути під 2 номером Н рівна
P2=2/5.
Наступну А ймовірність витягнути серед 4, що лишилося
P3=2/4.
Далі Н можна витягнути з ймовірністю
P4=1/3.
Чим ближче до кінця тим більша ймовірність, і вже А можемо витягнути при
P5=1/2.
Після цього залишається одна картка С, тому ймовірність її витягнути рівна 100 процентам або
P6=1.
Ймовірність скласти слово АНАНАС рівна добутку ймовірностей
P=3/6*2/5*2/4*1/3*1/2*1=1/60=0,016(6).
На цьому і базуються подібні завдання із теорії ймовірностей.
Завдання 3. З партії виробів товарознавець навмання вибирає зразки. Ймовірність того, що навмання узятий виріб опиниться вищого сорту рівна 0,8. Знайти ймовірність того, що серед 3 відібраних виробів буде два вироби вищого сорту?
Обчислення: Даний приклад на застосування формули Бернуллі.
p=0,8; q=1-0,8=0,2.
Ймовірність обчислюємо за формулою ![]()
Якщо пояснювати не мовою формул, то потрібно скласти комбінації з трьох подій, дві з яких сприятливі, а одна ні. Це можна записати сумою добутків
![]()
Обидва варіанти є рівносильні, тільки перший можемо застосувати в усіх завданнях, а другий в подібних до цього.
Завдання 4. З п'яти стрільців двоє попадають в ціль з ймовірністю 0,6 і троє з ймовірністю 0,4. Що вірогідніше: навмання вибраний стрілець попадає в ціль чи ні?
Обчислення: За формулою повної імовірності визначаємо ймовірність, що стрілець попаде.
P=2/5*0,6+3/5*0,4=0,24+0,24=0,48.
Ймовірність менша P<0,5, отже вірогідніше, що навмання вибраний стрілець не попаде у ціль.
Ймовірність, що не влучить становить
![]()
або
P=2/5*(1-0,6)+3/5*(1-0,4)=0,16+0,36=0,52.
Отже, робимо висновок, що вірогідніше стрілець не влучить.
Завдання 5. З 20 студентів, що прийшли на іспит, 10 підготовлені відмінно(знають всі питання), 7 добре(знають по 35 питань), а 3 погано (10 питань). У програмі 40питань. Навмання викликаний студент відповів на три питання квитка. Яка ймовірність того, що він підготовлений на
- а) відмінно;
- б) погано.
Обчислення: Суть задачі полягає в тому, що студент відповів на три питання квитка, тобто на всі що були задані, а от яка ймовірність їх витягнути ми зараз обчислимо.
Знайдемо ймовірність, що студент відповів на три питання. Це буде відношення кількості студентів до всієї групи помножене на ймовірність витягнути білети, що вони знають серед всієї їх кількості
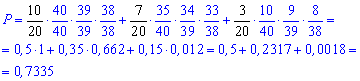
Тепер знайдемо ймовірність, що студент належить групі, що підготовлена на відмінно. Це рівносильно частці першого доданку попередньої ймовірності, до цієї ймовірності
![]()
б) Ймовірність, що студент належить групі, що погано підготувалася досить мала і рівна 0,00216.
![]()
На цьому завдання виконано. Добре його розберіть та запам'ятайте як обчислювати його, оскільки на контрольних і тестах воно поширене.
Завдання 6. Монету кидають 5 разів. Знайти ймовірність того, що герб падає менше 3 разів?
Обчислення: Ймовірність витягнути герб чи решку рівносильна і рівна 0,5. Менше 3 разів означає, що герб може випасти або 0, або 1, або 2 рази. "Або" завжди в ймовірності в операціях позначається додаванням.
Ймовірності знаходимо за формулою Бернуллі
![]()
Оскільки p=q=0,5, то ймовірність рівна
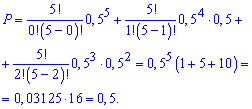
Ймовірність рівна 0,5.
Завдання 7. При штампуванні металевих клем виходить в середньому 90% стандартних. Знайти ймовірність того, що серед 900 клем стандартними будуть не менше 790 і не більше 820 клем.
Обчислення: Обчислення необхідно проводити за інтегральною теоремою Муавра-Лапласа.
Записуємо відомі величини
n=900; p=0,9; q=1-0,9=0,1; k1=790; k2=820.
Ймовірність знаходимо за формулою
![]()
де ![]() інтегральна функція Лапласа
інтегральна функція Лапласа
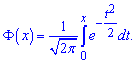
Значення x1, x2 обчислюємо за формулою
![]()
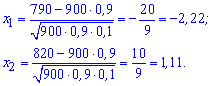
Далі знаходимо ймовірність, що серед 900 клем стандартними будуть не менше 790 і не більше 820 клем
![]()
Значення функції Лапласа беремо з таблиці.
Якщо поясните подібні завдання так як тут написано, то за контрольну з ймовірності отримаєте оцінку "відмінно".
ВАРІАНТ – 17
Завдання 1 Із урни, в якій 10 білих, 4 чорних та 5 синіх кульок, навмання вибирають три кульки. Знайти ймовірність того, що серед них будуть:
- а) всі білі;
- б) всі чорні;
- в) 1 біла, 1 синя, 1 чорна.
Розв'язання: На методиці вирішення таких задач зупинятися не будемо, нагадаємо лише, що кількість подій - сприятливих та можливих знаходимо через розміщення. Число всіх можливих подій за якими можна вибрати 3 кульки з 19 (10+4+5) рівне A193:
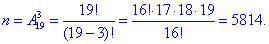
Формулу для факторіалів Ви повинні використовувати досить легко, оскільки майже всі формули теорії ймовірностей побудовані на факторіалах.
а) Число сприятливих подій за якими можна вибрати три білі кульки із 10 можливих рівна A103=720:
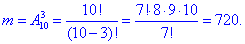
Ймовірність події A, при якій вибирають три кульки білого кольору знаходимо за класичною формулою рівна:
P(B)=m/n=720/5814=0,1238.
б) Кількість способів, за якими можна вибрати три чорні кульки із 4 можливих рівна A43: 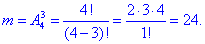
Знаменник завжди той самий, оскіьки кількість можливих варіантів вибрати три кульки ми знайшли на початку. Далі через частку m/n обчислюємо ймовірність події B, при якій вибирають три кульки чорного кольору:
P(B)=m/n=24/5814=0,0041.
в) Цей пункт на пратиці багато студентів виконує неправильно. Число сприятливих подій за якими можна вибрати 1 білу кульку з 10, 1 чорну кульку з 4 і 1 синю кульку з 5 знаходимо через добуток розміщень:
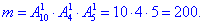
Ймовірність події C, при якій вибирають 1 білу, 1 чорну і 1 синю кульки рівна:
P(C)=m/n=200/5814=0,0344.
Якщо Ви читали відповіді до попередніх контрольних то мабуть зауважили, що є інший спосіб обчислити ймовірності.
Завдання 2 В продукції заводу брак складає 5% від загальної кількості деталей. Для контролю відібрано 20 деталей. Знайти ймовірність того, що серед відібраних
- а) одна бракована;
- б) не більше чотирьох бракованих;
- в) жодна не бракована.
Розв'язання: Ймовірність відбирання бракованих деталей змінюється за біноміальним законом, де n=20, p=0,05, q=1-p=0,95:
Формула розподілу ймовірностей має вигляд
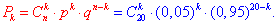
а) Ймовірність того, що серед відібраних одна бракована k=1:
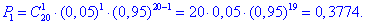
б) Ймовірність того, що серед відібраних не більше чотирьох бракованих – це означає або 0, або 1, або 2, або 3, або4 бракованих:
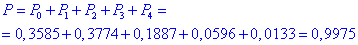
Умова "або" при обчисленні ймовірності виражається знаком додавання, а не множення. Це вивчіть і застосовуйте де потрібно.
в) Ймовірність того, що серед відібраних жодна не бракована означає 0 з 20: 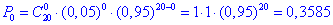
Ось такими легкими можуть бути відповіді, якщо знаєте формули.
Завдання 3 На контроль надійшли вироби, які виготовлені трьома робітниками. Перший виготовив 30 виробів, серед яких 7% браку, другий – 50 виробів, серед яких 4% браку, а третій – 40, серед яких 3% браку. Взятий навмання виріб – доброякісний. Знайти ймовірність того, що виріб виготовив 2-й робітник.
Розв'язання: Ви повинні знати, що така задача розв'язується через формулу повної ймовірності та Байєса. Якщо не знаєте назви формул, то хоч запам'ятайте наступну методику.
Позначаємо через Hi - гіпотези, що виріб виготовлений і-м робітником, де i=1,2,3. Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності:
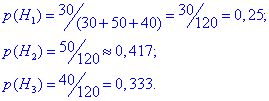
Їх сума повинна бути рівна повній ймовірності (1). Якщо не так, значить Ви або чогось не врахували або допустили помилку.
Далі подія A полягає в тому, що взятий навмання виріб доброякісний. На основі умови можемо виписати ймовірності того, що доброякісний виріб виготовив кожен із робітників:
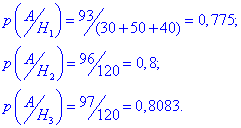
За формулою повної ймовірності знаходимо ймовірність, що виріб доброякісний:
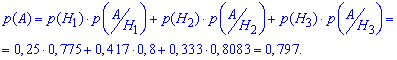
Це по суті сума вкладів кожного з робітників помножена на якість виробів.
Ймовірність того, що виріб виготовив 2-й робітник за формулою Байєса рівна 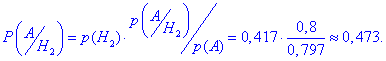
Якщо проаналізувати попередню формулу, то це вклад другого доданку в знайдену ймовірність.
Завдання 4 Вважаючи, що ймовірність навчатися у ВУЗі для хлопців та дівчат рівна, знайти ймовірність того, що серед 300 студентів:
- а) 200 дівчат;
- б) не менше 100 і не більше 170 дівчат.
Розв'язання: а) Оскільки ймовірність навчатися у ВУЗі для дівчат і хлопців рівна p=0,5, то за формулою Бернуллі знаходимо точне значення
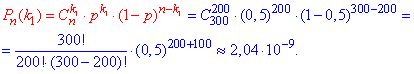
Без знання математичних програм таке значення знайти важо, інженерні калькулятори при високих показниках (300) дають похибку.
Єдиний можливий варіант - знайти наближене значення за локальною теоремою Лапласа.
Оскільки умова застосування формул виконується n*p*q=300*0,5*0,5=75>10, то похибка обчислень мінімальна
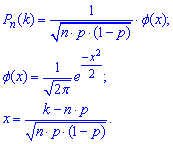 Виконаємо обчислення аргумента функції Лапласа:
Виконаємо обчислення аргумента функції Лапласа:
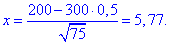
За таблицями табулювання локальної функції Лапласа маємо phi
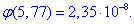
Підставляємо та знаходимо ймовірність
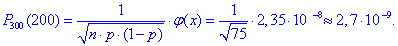
Зважаючи на показник степеня при основі 10, розбіжність зі значенням отриманим за формулою Бернуллі незначне!
б) Ймовірність, що не менше 100 і не більше 170 дівчат у ВУЗі знайдемо за інтегральною формулою Лапласа:
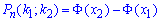 де
де 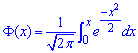 - інтегральна функція Лапласа;
- інтегральна функція Лапласа;
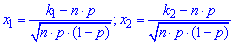 - аргументи інтегральної функції розподілу.
- аргументи інтегральної функції розподілу.
Знайдемо дві точки
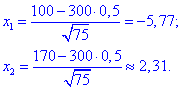
Далі значення інтегральної функції Лапласа в x1, x2 підставляємо в формулу ймовірності 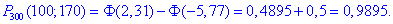
Завдання 5 В партії 20% нестандартних деталей. Навмання вибрані чотири з них (n=4). X - число стандартних серед відібраних. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення 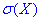 , функцію розподілу F(X) та побудувати її графік.
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Умова "В партії 20% нестандартних деталей" означає, що від досліду до досліду ймовірність залишається сталою, а саме p=0,8 і q=1-p=0,2.
Таким чином ймовірність відбирання стандартних деталей змінюється за біноміальним законом:
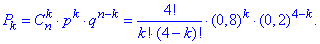
Результати розрахунків запишемо в таблицю розподілу ймовірностей:
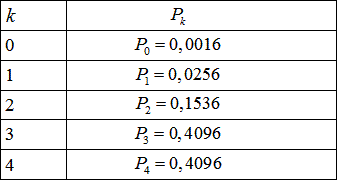 Будуємо графік закону розподілу (щіьності)
Будуємо графік закону розподілу (щіьності)
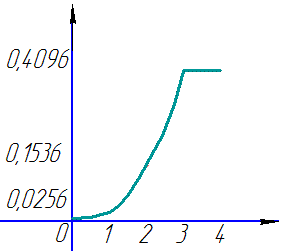 Математичне сподівання випадкової величини рівне
Математичне сподівання випадкової величини рівне
M(X)=n*p=4*0,8=3,2.
Дисперсію знаходимо за формулою
D(X)=n*p*q= 4*0,8*0,2=0,64.
Через корінь квадратний з дисперсії визначаємо середнє квадратичне відхилення випадкової величини X:
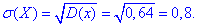
Функцію розподілу випадкової величини X знаходимо за формулою:
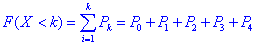
Результати обчислень записуємо у таблицю:
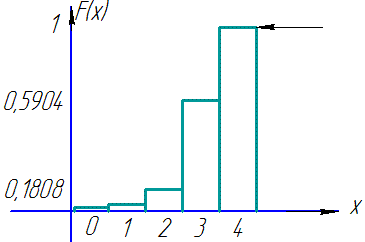
 За знайденими значеннями будуємо графік функції розподілу ймовірностей
За знайденими значеннями будуємо графік функції розподілу ймовірностей
 На цьому приклад розв'язано.
На цьому приклад розв'язано.
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
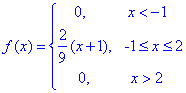 Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Розв'язання: Функція розподілу обчислюємо інтегруванням f(x):
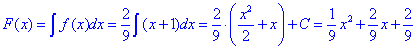
В результаті отримаємо сталу справа, яку довизначаємо умовою F(b)=1:
F(2)=1 -> C=2/9.
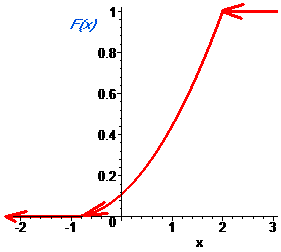
Будуємо графік щільності розподілу f(x):
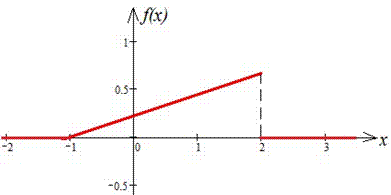 та функції розподілу ймовірностей F(x) (при C=2/9)
та функції розподілу ймовірностей F(x) (при C=2/9)
 Через інтеграл по проміжку обчислюєио математичне сподівання
Через інтеграл по проміжку обчислюєио математичне сподівання
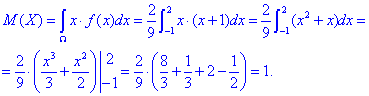
та дисперсію:
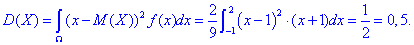
Інтеграли в ймовірності не складні, тому детально їх розписувати не будемо.
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b) рівна інтегралу:
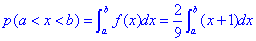
Його значення визначте самостійно.
Завдання 7 Відомі математичне сподівання a=15 та середнє квадратичне відхилення 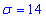 випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
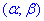 =(0;30);
=(0;30); - б) абсолютна величина відхилення |x-a|<11 буде менше за
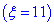
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 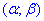 скористаємось формулою Лапласа:
скористаємось формулою Лапласа:
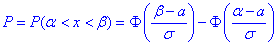
де 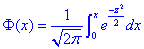 - інтегральна функція Лапласа (її значення є в таблиці).
- інтегральна функція Лапласа (її значення є в таблиці).
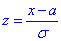 - заміна змінних в експоненті.
- заміна змінних в експоненті.
Отож, знаходимо значення в точках та підставляємо в формулу ймовірності
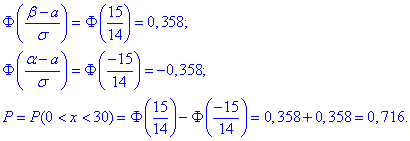
Значення Ф(х) беремо з таблиці, або визначаємо в Maple, Mathematica, MathCad.
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<11 буде менше за 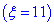 скористаємось простою залежністю:
скористаємось простою залежністю:
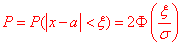 Знахоимо єдине значення функції Лапласа
Знахоимо єдине значення функції Лапласа
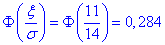
та обчислюємо ймовірність, що абсолютна величина відхилення буде менша 11
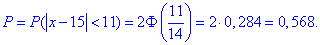
На цьому розв'язування контрольної з теорії ймовірностей завершено. Готові відповіді до контрольних на ймовірності та задач з інших тем шукайте на сторінках сайту.
Варіант 13 . Індивідуальне завдання 2.
Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею:
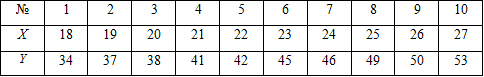
Записати вибіркове рівняння прямої регресії Y на X.
Розв'язання:
Обчислюємо згідно формул ймовірності потрібні величини для складання вибіркового рівняння регресії:
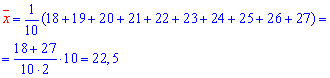
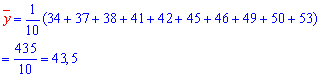
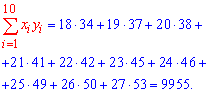
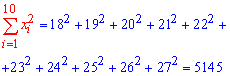
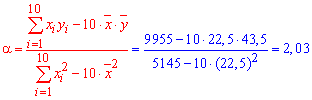
Отже, вибіркове рівняння регресії y=2,03*x-2,175.
Обчислимо вибірковий коефіцієнт кореляції:
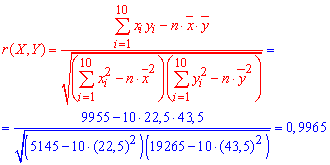
Оскільки вибірковий коефіцієнт кореляції
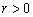 , тому зв'язок між Х і У є додатний і ці випадкові величини збільшуються одночасно.
, тому зв'язок між Х і У є додатний і ці випадкові величини збільшуються одночасно.
Завдання 2. Знайти інтервал довіри для оцінки з надійністю ![]() невідомого математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності: а) якщо
невідомого математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності: а) якщо![]() =0,96, генеральне середнє квадратичне відхилення
=0,96, генеральне середнє квадратичне відхилення ![]() =5,0, вибіркове середнє
=5,0, вибіркове середнє ![]() =21,0, а обсяг вибірки n=36; б) якщо
=21,0, а обсяг вибірки n=36; б) якщо ![]() =0,99, підправлене середнє квадратичне відхилення s=6,0, вибіркове середнє
=0,99, підправлене середнє квадратичне відхилення s=6,0, вибіркове середнє ![]() =45,0, а обсяг вибірки n=9.
=45,0, а обсяг вибірки n=9.
Розв'язання:
а) З рівняння ![]() за допомогою функції Лапласа методом інтерполяції знаходимо
за допомогою функції Лапласа методом інтерполяції знаходимо
![]()
Межі інтервалу довіри шукаємо за формулами:
![]()
![]()
Отже, інтервал довіри рівний ![]() з надійністю
з надійністю ![]() =0,96.
=0,96.
б) Оскільки обсяг вибірки менший 30 (n=9<30) і середнє квадратичне відхилення ![]() невідоме, то для знаходження меж інтервалу довіри використаємо формулу
невідоме, то для знаходження меж інтервалу довіри використаємо формулу
![]()
де значення ![]() шукаємо за допомогою таблиць (розподіл Ст'юдента):
шукаємо за допомогою таблиць (розподіл Ст'юдента):
![]()
![]()
![]()
Після обчислень інтервал довіри рівний ![]() з надійністю 0,99.
з надійністю 0,99.
Завдання 3. Знайти інтервал довіри для оцінки з надійністю ![]() =0,95 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=11, а підправлене середнє квадратичне відхилення s=9,3.
=0,95 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=11, а підправлене середнє квадратичне відхилення s=9,3.
Розв'язання:
Задача зводиться до відшукання інтервалу довіри ![]() , який покриває
, який покриває ![]() з заданою надійністю
з заданою надійністю ![]() =0,95.
=0,95.
За таблицею знаходимо ![]()
Шуканий інтервал довіри ![]() або
або
![]()
Як бачите обчислення під силу кожному, головне вміти користуватися формулами та таблицями (розподіл Ст'юдента) . Перевірка гіпотез буде розглянута в наступній статті.
Практикум з ТМС. Варіант-8
Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею: 
Записати вибіркове рівняння прямої регресії Y на X.
Розв'язання: Для побудови прямої регресії Y на X слід спершу знайти середнє значення кожної з ознак:
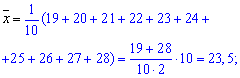
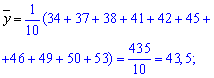
Далі суму їх попарних добутків
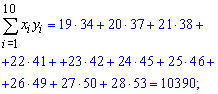
та квадратів значень ознаки X
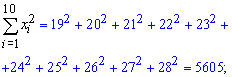
Після цього можемо порахувати самі коефіцієнти, що фігурують в рівнянні регресії
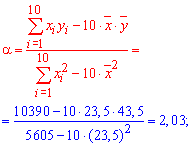
![]()
Ну і сама легша частина - це все підставити у рівняння y=2,02*x-4,205. З вигляду формул бачимо, що надзвичайно складних операцій виконувати тут не приходиться. Однак і тут багато хто з Вас умудряється наробити помилок.
Для підтвердження лінійного зв'язку між ознаками Y на X слід ще знайти вибірковий коефіцієнт кореляції:
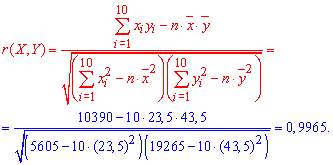
Чим він ближче до одиниці, тим краще лінійна функція описує залежність між ознаками. В нашому випадку вибірковий коефіцієнт кореляції r(X, Y) практично співпадає з одиницею, тому робимо висновок, що припущення про лінійність зв'язку між X і Y правильне. Також r>0, що свідчить про додатний зв'язок між X і Y,є тобто ці випадкові величини збільшуються одночасно.
Завдання 2. Знайти інтервал довіри для оцінки з надійністю γ невідомого математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності:
- а) якщо γ=0,96, генеральне середнє квадратичне відхилення σ=5,0, вибіркове середнє
 =28,0, а обсяг вибірки n=25;
=28,0, а обсяг вибірки n=25; - б) якщо γ=0,99, підправлене середнє квадратичне відхилення s=12,0, вибіркове середнє
 =65,0, а обсяг вибірки n=16.
=65,0, а обсяг вибірки n=16.
Розв'язання: а) З рівняння ![]() за допомогою функції Лапласа методом інтерполяції із сусідніх значень знаходимо
за допомогою функції Лапласа методом інтерполяції із сусідніх значень знаходимо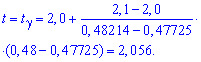
Межі інтервалу довіри знаходимо із формулами:
![]()
![]()
Записуємо інтервал довіри
![]()
з надійністю
![]()
б) Оскільки n=16<30 і середнє квадратичне відхилення  невідоме, то для знаходження меж інтервалу довіри використаємо формулу
невідоме, то для знаходження меж інтервалу довіри використаємо формулу
![]() ,
,
де значення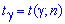 шукаємо за допомогою таблиць (розподіл Ст'юдента):
шукаємо за допомогою таблиць (розподіл Ст'юдента):
![]()
![]()
![]()
Отже, інтервал довіри рівний ![]() з надійністю
з надійністю ![]() .
.
Завдання 3. Знайти інтервал довіри для оцінки з надійністю γ=0,99 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=35, а підправлене середнє квадратичне відхилення s=10,3.
Розв'язання: Задача зводиться до відшукання інтервалу довіри 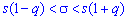 , який покриває
, який покриває  з заданою надійністю
з заданою надійністю 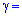 0,99.
0,99.
За таблицею функції q знаходимо
![]()
Шуканий інтервал довіри лежить в межах
![]()
або
![]()
Дочитайте відповіді до кінця і теорія ймовірності стане для Вас зрозуміліша і доступна.
Контрольна робота №1. ВАРІАНТ – 16
Завдання 1 Навмання складається букет із трьох квіток. Серед квіток є 6 айстр, 5 троянд та 3 ромашки.
Знайти ймовірність того, що букет складається:
- а) із трьох троянд;
- б) із трьох ромашок;
- в) із 1 троянди, 1 ромашки та 1 айстри.
Розв'язання: Схема обчислень такого сорту задач з ймовірності полягає в знаходженні числа всіх можливих подій, далі числа сприятливих подій. Сама ймовірність рівна відношенню цих чисел p=m/n.
При такому формулюванні обчислення проводимо через формулу розміщень
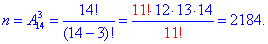
Уважно перегляньте, як спростовувати факторіали в дробі.
а) Число сприятливих подій рівна кількость способів, за якими можна вибрати 3 троянди із 5 можливих (розміщення з 5 по 3):
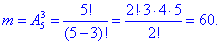
Ймовірність скласти букет із трьох троянд рівна:
P(A)=m/n=60/2184=0,0275.
б) Число способів, за якими можна вибрати 3 ромашки із 3 можливих рівне m=3*2*1=6.
Ймовірність склаcти букет з трьох ромашок рівна частці чисел:
P(B)=6/2184=0,00275.
в) Число сприятливих подій, за якими можна вибрати 1 троянду з 5, 1 ромашку з 3 і 1 айстру з 6 рівне добутку відповідних розміщень:
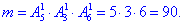
Ймовірність події C, при якій складають букет із 1 троянди, 1 ромашки та 1 айстри рівна:
P(C)=m/n=90/2184=0,0412.
Дану задачу можна розв'язати другим способом.
а) Маємо 14 квіток, потрібно вибрати 3 троянди з 5. Першу можна вибрати з ймовірністю p1=5/14, після того залишиться 4 троянди і 13 квіток. Тоді другою троянду можна витягнути з ймовірністю p2=4/13, і 3 троянду в букеті з ймовірністю p3=3/12. Ймовірнысть скласти букет із трьох троянд рівна добутку ймовірностей
p=p1*p2*p3=5/14*4/13*3/12= 5/182=0,0275.
Методика не складна і її під силу вивчити за кілька прикладів.
б) Для цього пункту важливо, що маємо 3 ромашки з 14 квітів, а букет має містити всі 3 ромашки. Не розписуючи всі міркування, знайдемо ймовірність за попередньою схемою
p=p1*p2*p3=3/14*2/13*1/12= 1/364=0,00275.
в) Ймовірність буде рівна добутку часток квітів, при цьому слід враховувати, що їх кількість буде зменшуватися на одиницю при кожному виборі
p=p1*p2*p3=5/14*3/13*6/12= 15/364=0,0412.
При цьому порядок вибору квітів (перша троянда чи третя) не змінює ймовірність скласти з них букет.
Завдання 2 Студент знає 20 питань із 25 програми. Знайти ймовірність, що студент із трьох запитань відповів:
- а) на одне запитання;
- б) на всі запитання;
- в) не відповів на жодне.
Розв'язання: Число можливих способів, за якими можна вибрати 3 запитання із 25, тобто кількість різних білетів знаходимо за формулою розміщень:
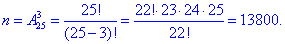
а) Число способів, за якими студент відповів на одне запитання з 3 рівне добутку розміщень:
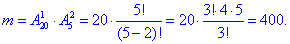
Перше з них означає, що вибираємо 1 питання з 20 на які студент знає відповідь, друге- кількість варіантів вибрати 2 питання з 5.
Ймовірність події A, при якій студент відповів на одне запитання з 3 рівна частці:
P(A)=m/n=400/13800=0,029.
б) Число способів, за якими можна вибрати білет із 3 запитанням, на які він знає відповідь рівна розміщенню з 20 по 3:
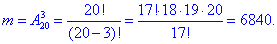
Ймовірність такої події B знаходимо за класичною формулою:
P(B)=m/n=6840/13800=0,4957.
в) Останнє значення ймовірності приймає найменше з усіх значень. А все тому, що студент вивчив більшість питань на екзамен, і лише є 60 способів витягнути 3 питання з 5 , на які він не знає відповіді:
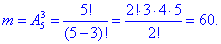
Ймовірність події C, при якій студент не відповів на жодне запитання рівна:
P(B)=m/n=60/13800=0,0043.
Ось і всі пояснення до задачі.
Завдання 3 На контроль надійшли вироби, які виготовлені трьома робітниками. Перший виготовив 20 виробів, серед яких 4% браку, другий – 30 виробів, в яких 1% браку, а третій – 50, серед яких 5% браку. Взята навмання деталь виявилась бракованою.
Знайти ймовірність того, що виріб виготовив 3-й робітник.
Розв'язання: Задачу обчислюємо за формулою повної ймовірності та Байєса. За першою знаходимо ймовірність витягнути браковану деталь, за Байєсом - ймовірність виготовлення бракованої деталі 3 робітником.
Позначимо через Hi - гіпотези, що виріб виготовлений і-м робітником (i=1,2,3).
Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності:
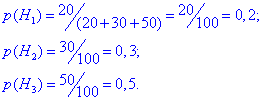
Сума ймовірностей повинна бути рівна одиниці. Якщо у Вас в сумі не виходить одиниця, значить Ви вже "накосячили", шукайте помилку.
Нехай подія A полягає в тому, що взята навмання деталь бракована. Тоді на основі умови можемо виписати ймовірності того, що браковану деталь виготовив кожен робітник:
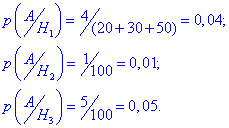
За формулою повної ймовірності знаходимо ймовірність, що деталь бракована: 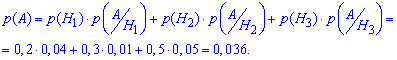
Ймовірність що браковану деталь виготовив 3-й робітник знаходимо за формулою Байєса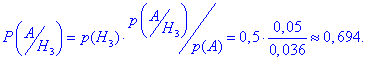
Вона рівна частці третього доданку в попередньо знайденій ймовірності.
Завдання 4 Ймовірність попадання в мішень при одному пострілі 0,6. Знайти ймовірність того, що при 250 пострілах в мішень попали:
- а) 100 разів;
- б) не менше 150 і не більше 200.
Розв'язання: а) Завдання на вигляд просте, однак багато з Вас розгубиться, якщо таку задачу розмістити серед простеньких. Для седе запам'ятайте, що при великій кількості випробувань + треба знайти ймовірність попадання в проміжок - це вже підказка застосовувати локальну та інтегральну теорему Лапласа. Якщо, наприклад, мені потрібно знайти точну відповідь на питання б) то в Maple чи іншому мат. пакеті я можу 50 раз застосувати формулу Бернуллі, яка дає найточніше значення, а далі все просумувати.
Проблема в тому, що при теперішньому рівні компютеризації Вас всіх вчат по таблицях шукати наближені значення функцій Лапласа, замість вчити обчислювати їх та всі формули, що є в теорії ймовірностей в математичних пакетах.
Оскільки ймовірність не залежить від історії (попередніх пострілів), то за формулою Бернуллі знаходимо точне значення
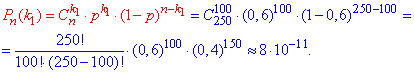 Однак його ми точно знайшли не калькулятором, оскільки при піднесенні до 100 і 150 степеня похибка була б великою.
Однак його ми точно знайшли не калькулятором, оскільки при піднесенні до 100 і 150 степеня похибка була б великою.
Вам же потрібно швидко оцінити ймовірність, тому наближене її значення знаходимо за локальною теоремою Лапласа.
Оскільки умова застосування формули Лапласа n*p*q=250*0,6*0,4=60>10 виконується, то відхилення від точного значення має бути мінімальним
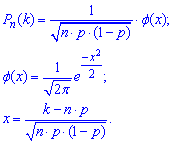
Виконаємо обчислення x:
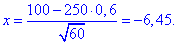
За таблицями табулювання локальної функції Лапласа маємо phi
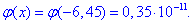
і саме значення ймовірності
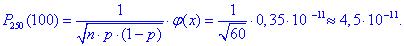 Порівнюючи показники степеня при основі (-11) робимо висновок, що розбіжність з формулою Бернуллі невелика!
Порівнюючи показники степеня при основі (-11) робимо висновок, що розбіжність з формулою Бернуллі невелика!
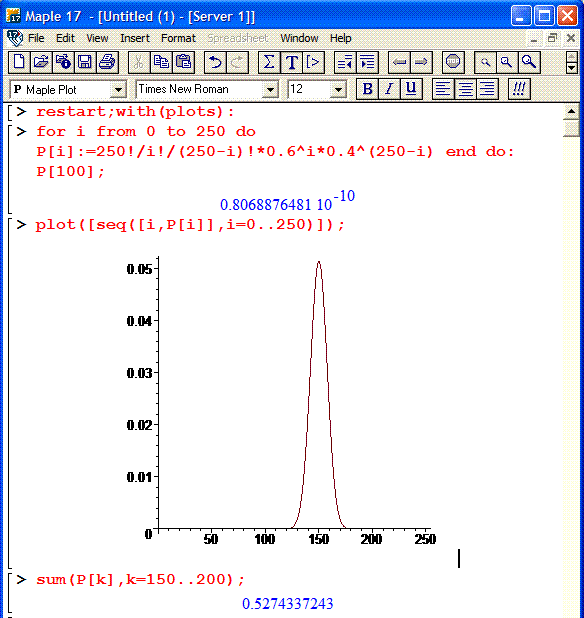
б) Ймовірність, що не менше 150 і не більше 200 попали в мішень при 250 пострілах знайдемо за інтегральною формулою Лапласа:
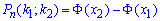
де 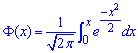 - інтегральна функція Лапласа;
- інтегральна функція Лапласа;
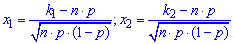 - аргументи інтегральної функції розподілу.
- аргументи інтегральної функції розподілу.
Знайдемо точки x1=0, x2=6,45
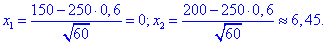
та виконуємо кінцеві обчислення
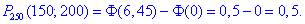
Щоб розв'язати задачу з теорії ймовірностей в Maple достатньо наступного коду
в результаті отримаємо всі потрібні значення + графік розподілу ймовірнотей
> restart;with(plots):
> for i from 0 to 250 do P[i]:=250!/i!/(250-i)!*0.6^i*0.4^(250-i) end do:
> P[100];
0.8068876481*10-10
> plot([seq([i,P[i]],i=0..250)]);
> sum(P[k],k=150..200);
0.5274337243
Щоб переконати Вас, що все насправді так легко наведу Вам фрагмент розрахунків
Завдання 5 В партії 10% нестандартних деталей. Взято чотири (n=4). X - число нестандартних серед відібраних. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення 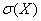 , функцію розподілу F(X) та побудувати її графік.
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність не змінюється (а саме p=0,1 і q=1-p=0,9), то відбирання нестандартних деталей змінюється за самим поширеним серед інших біноміальним законом:
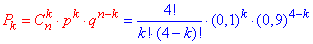
Результати для 4 деталей запишемо у таблицю:
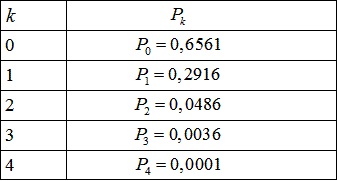 Графік закону розподілу має вигляд
Графік закону розподілу має вигляд
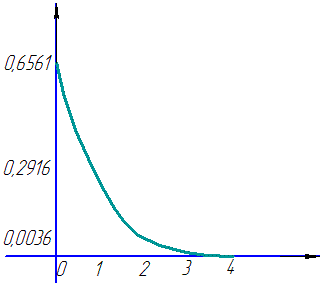 Математичне сподівання випадкової величини M(X)=n*p=4*0,1=0,4.
Математичне сподівання випадкової величини M(X)=n*p=4*0,1=0,4.
Дисперсія D(X)=n*p*q= 4*0,1*0,9=0,36.
Середнє квадратичне відхилення випадкової величини X:
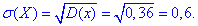
Функцію розподілу випадкової величини X знайдемо за формулою:
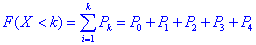
Результати запишемо в таблицю:
 Графік функції розподілу має вигляд
Графік функції розподілу має вигляд
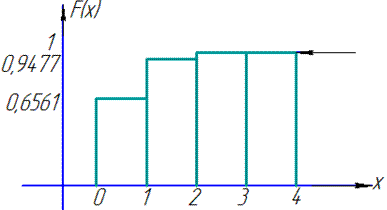 На цьому задача розв'язана.
На цьому задача розв'язана.
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
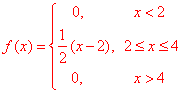
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Розв'язання: Функцію розподілу знаходимо через інтеграл від щільності:
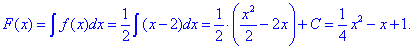
Сталу інтегрування знаходимо з умови, що функція розподілу на кінці рівна одиниці F(4)=1.
Пам'ятайте про те, що вона повинна приймати значення выд 0 до одииці і бути неперервною.
Звідси 4-4+С=1, С=1.
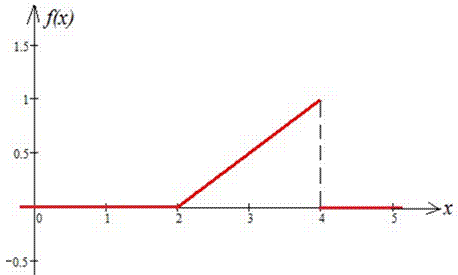
Графік щільності f(x) та функції розподілу F(x) навдено нижче:
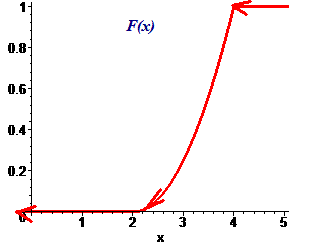 Математичне сподівання знахидомо інтегруванням:
Математичне сподівання знахидомо інтегруванням:
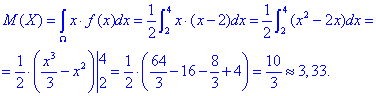
Дисперсію через інтеграл обчислюємо за формулою:
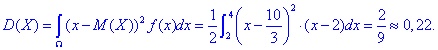
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b) рівна інтегралу:
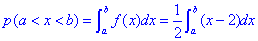
Його значення обчисліть самостійно.
Завдання 7 Відомі математичне сподівання a=12 та середнє квадратичне відхилення 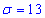 випадкової величини x, яка розподілена нормально.
випадкової величини x, яка розподілена нормально.
Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
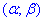 =(10;20);
=(10;20); - б) абсолютна величина відхилення |x-a|<6 буде менше за
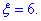
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 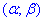 скористаємось інтегральною формулою Лапласа :
скористаємось інтегральною формулою Лапласа :
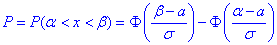
На краях інтервалу отримаємо такі значення
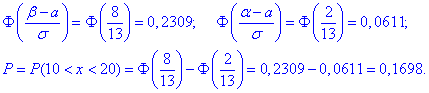
Просумувати їх не складає великих проблем.
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<6 буде менше за 6 скористаємось формулою:
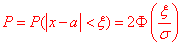
З таблиці знаходимо значення
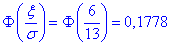
та множимо його на 2
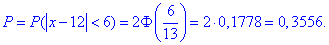
Це і буде ймовірність, що абсолютна величина відхилення менша за 6.
На цьому розбір контрольної завершено, більше готових відповідей на типові задачі з теорії ймовірностей шукайте на сторінках сайту.
ВАРІАНТ – 12
Завдання 1 В ящику 25 деталей, серед яких 10 кольорових. Навмання витягують 5 деталей.
Знайти ймовірність того, що серед взятих деталей:
- а) всі кольорові;
- б) всі некольорові;
- в) 2 кольорові та 3 некольорові.
Розв'язання: Кількість всіх можливих подій – всі можливі способи, за якими можна вибрати 5 деталей з 25. Їх знаходимо через формулу розміщень з комбінаторики: 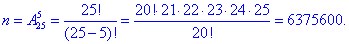
а) Число сприятливих подій – всі способи, за якими можна вибрати 5 кольорових із 10 можливих.
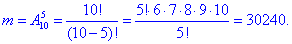
Ймовірність події A, при якій витягують 5 кольорових деталей рівна відношенню сприятливих подій до всіх можливих p=m/n:
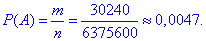
Поки що нічого важкого немає і пояснення Вам мають бути зрозумілими. Якщо ж ні то почитайте основи комбінаторики, оскільки далі приклади будуть складнішими.
б) Через розміщення знаходимо кількість способів, за якими можна вибрати 5 некольорових деталей з 15 можливих:
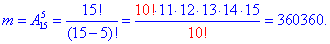
Уважно перегляньте, як потрібно розписувати факторіали, щоб швидко спростити спільні множники в чисельнику та знаменнику дробу.
Ймовірність події B, при якій витягують 5 некольорових деталей рівна частці чисел:
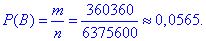
в) Число способів, за якими можна вибрати 2 кольорові деталі з 10 і 3 некольорові деталі з 15 знаходимо через добуток:
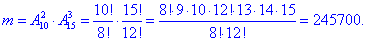
Ймовірність події C, при якій витягують 2 кольорові і 3 некольорові деталі рівна:
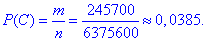
Завдання 2 Ймовірність непопадання в ціль для 1-го стрільця дорівнює 0,2; для 2-го – 0,1; для 3-го – 0,3. Обчислити ймовірність попадання в ціль:
- а) хоча б одного;
- б) двох;
- в) всіх.
Розв'язання: Позначимо ймовірність попадання в ціль кожного стрільця відповідно:
p1=0,2; p2=0,1; p3=0,3 .
Тоді ймовірність непопадання в ціль дорівнює відповідно:
q1=1-p1=0,8; q2=1-p2=0,9; q3=1-p3=0,7.
а) Ймовірність попадання в ціль хоча б одного є протилежною подією до такої, що ніхто з них не попав в ціль:
p=1-q1*q2*q3=1-0,8*0,9*0,7=1-0,504=0,496.
В іншому випадку Вам доведеться шукати багато добутків з "або". Це довший шлях, тому такі моменти запам'ятовуйте і тримайте як еталон.
б) Ймовірність попадання в ціль двох стрільців означає, що два попали в ціль, а третій з них – ні, ймовірність дорівнює сумі таких комбінацій:
p=p1*p2*q3+p1*q2*p3+q1*p2*p3=0,2*0,1*0,7+0,2*0,9*0,3+0,8*0,1*0,3=0,014+0,054+0,024=0,092.
Чому саме так проаналізуйте самостійно.
в) Ймовірність попадання в ціль всіх стрілків є добутком сприятливих ймовірностей:
p=p1*p2*p3=0,2*0,1*0,3=0,006.
На цьому завдання виконано, переходимо до наступної теми.
Завдання 3 Для 10 студентів 1-ї групи ймовірність скласти іспит дорівнює 0,9; для 12 (2-га група) – 0,6; для 15 (3-тя група) – 0,8. Навмання викликаний студент склав іспит.
Знайти ймовірність того, що студент, що склав іспит, належить до 2-ї групи.
Розв'язання: Задачі наведеного формулювання розраховують за формулами повної ймовірності та Байєса. Позначимо через Hi - гіпотези, що студент, який склав іспит належить до і-ї групи, де i=1,2,3. Тоді ймовірність кожної з гіпотез пропорційна частці студентів у кожній групі:
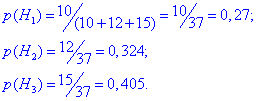
Самостійно переконайтеся, що їх сума рівна повній ймовірності.
Нехай подія A полягає в тому, що навмання викликаний студент склав іспит.
Тоді на основі умови можемо виписати ймовірності того, що цей студент належить до кожної групи: 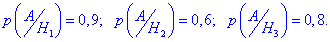
Далі за формулою повної ймовірності обчислюємо ймовірність, що студент склав іспит: 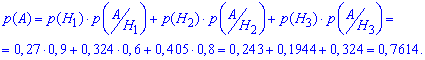
Формула не складна і тут важко помилитися в обчисленнях.
Ймовірність того, що студент, що склав іспит належить до 2-ї групи знаходимо за формулою Байєса 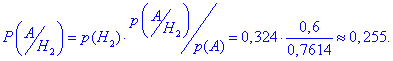
Це фактично вклад другого доданка в попередньо знайденій ймовірності.
Завдання 4 Ймовірність появи події в кожному із 900 незалежних експериментів дорівнює 0,5. Знайти ймовірність того, що подія з'явиться:
- а) рівно 450 разів;
- б) не менше 50 та не більше 350.
Розв'язання: а) Маємо справу з незалежними випробуваннями, тому ймовірність в кожному новому експерименті не залежить від попередньої історії (попередніх дослідів). Точне значення знаходимо за формулою Бернуллі
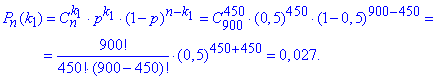
Оскільки степінь 450 досить великий, то обчислювати можливо лише в математичному пакеті. Простий чи інженерний калькулятор накопичує високу похибку при обчисленнях.
Наближене значення ймовірності можемо оцінити за локальною теорема Лапласа. Оскільки необхідна умова її застосування виконується
n*p*q=900*0,5*0,5=225>10, то похибка формул мінімальна
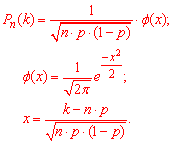
Виконаємо обчислення змінної: 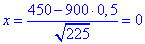
За таблицями табулювання локальної функції Лапласа виписуємо значення функції 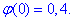
а далі знаходимо ймовірність
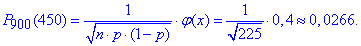
Як можете переконатися, розбіжність із точним значенням отриманим за формулою Бернуллі невелика!
б) Ймовірність, що не менше 50 і не більше 350 разів з'явиться подія знайдемо за інтегральною формулою Лапласа:
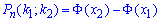
де 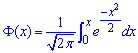 - інтегральна функція Лапласа;
- інтегральна функція Лапласа;
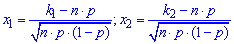 - аргументи інтегральної функції розподілу.
- аргументи інтегральної функції розподілу.
Обчислюємо точки
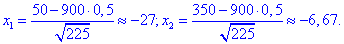
Отож за таблицею значень інтегральної функції Лапласа знаходимо ймовірність в точках та обчислюємо
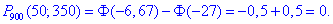
Наведений інтеграл неважко знайти в математичних пакетах Maple, Mathematica, MathCad, MatLab.
Завдання 5 Зроблено чотири постріли в ціль (n=4). Ймовірність попадання при одному пострілі 0,6. X - число попадань. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення 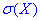 , функцію розподілу F(X) та побудувати її графік.
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність залишається постійною (а саме p=0,6 і q=1-p=0,4), то ймовірність попадання в ціль змінюється за біноміальним законом розподілу: 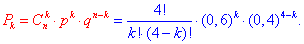 Результати запишемо в таблицю:
Результати запишемо в таблицю:
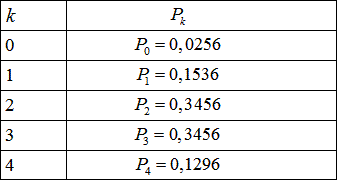 Графік закону розподілу має вигляд
Графік закону розподілу має вигляд
 Знаходимо математичне сподівання випадкової величини
Знаходимо математичне сподівання випадкової величини
M(X)=n*p=4*0,6=2,4.
Обчислюємо дисперсію
D(X)=n*p*q= n*p*q=4*0,6*0,4=0,96.
Середнє квадратичне відхилення випадкової величини X знаходимо через корінь з дисперсії:
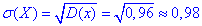
Функцію розподілу випадкової величини X обчислюємо за формулою:
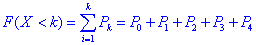
Результати записуємо в таблицю:
 Графік функції розподілу має вигляд
Графік функції розподілу має вигляд
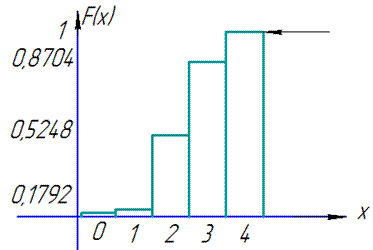 На цьому розбір завдання завершено.
На цьому розбір завдання завершено.
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
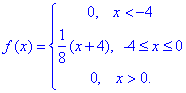
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань X набуде значень, що належать інтервалу (a;b).
Побудувати графіки f(x) та F(X).
Розв'язання: Функцію розподілу обчислюємо інтегруванням: 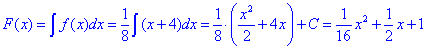
Константу, що фігурує довизначаємо з умови, що на кінці проміжку функція розподілу рівна 1.
Звідси маємо F(0)=1, C=1.
Графіки функцій f(x) та F(X) наведено нижче
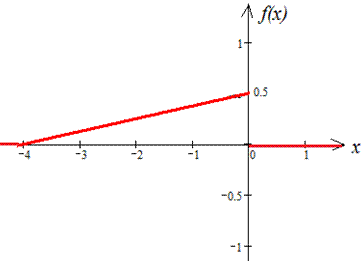
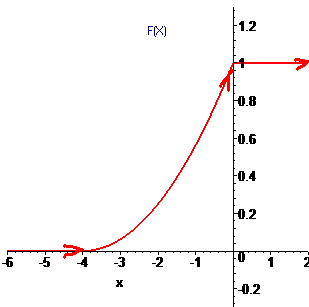
Знаходимо математичне сподівання:
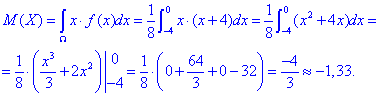 .
.
Далі дисперсію:
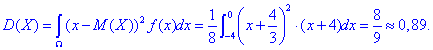
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b):
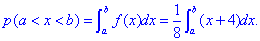
Завдання 7 Відомі математичне сподівання a=8 та середнє квадратичне відхилення 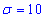 випадкової величини x, яка розподілена нормально.
випадкової величини x, яка розподілена нормально.
Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
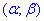 =(0;20);
=(0;20); - б) абсолютна величина відхилення |x-a|<16 буде менше за 16
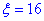
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 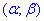 скористаємось формулою:
скористаємось формулою:
де 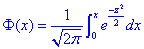 - інтегральна функція Лапласа (її значення знаходимо в таблиці).
- інтегральна функція Лапласа (її значення знаходимо в таблиці).
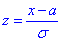 - заміна змінних.
- заміна змінних.
Знаходимо значення функцій та ймовірність
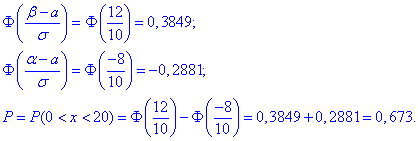
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<16 буде менше за 16 (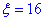 ) скористаємось формулою:
) скористаємось формулою:
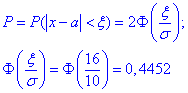
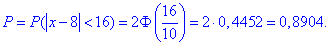
Формули не складні, як користуватися таблицями табулюванyя локальної та інтегральної функції Лапласа Вас на практиці мали навчити. Все решта зводиться до елементарних операцій.
ВАРІАНТ – 1
Завдання 1 Із коробки, в якій 10 білих, 6 чорних та 4 синіх кульок, навмання виймають 3 кульки. Знайти ймовірність того, що серед них будуть:
- а) всі білі;
- б) перша біла, далі дві чорні;
- в) одна біла, одна чорна, одна синя.
Розв'язання: Число всіх можливих подій – кількість способів, за якими можна вибрати 3 кульки з 20 (10+6+4) знаходимо через розміщення:
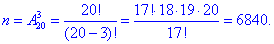
а) Число сприятливих подій – кількість способів, за якими можна вибрати 3 білі кульки з 10 можливих:
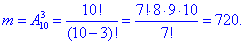
Ймовірність події A, при якій виймають усі білі кульки рівна
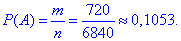
б) Число сприятливих подій – кількість способів, за якими можна вибрати одну білу кульку з 10 і дві чорних кульок з 6 можливих:
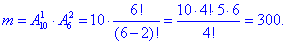
Ймовірність події B, при якій виймають 1 білу і дві чорні кульки:
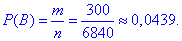
в) Число сприятливих подій – кількість способів, за якими можна вибрати 1 білу з 10, 1 чорну з 6 і 1 синю кульку з 4:
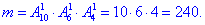
Ймовірність події C, при якій виймають 1 білу, 1 чорну і 1 синю кульки:
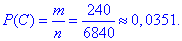
Наведені відповіді є правильними згідно формул теорії ймовірності, однак не так очевидними для студентів та школярів, важка для розуміння є методика обчислення. Існує геометричний спосіб вирішення даної задачі. Покажемо його переваги.
а) Для першого пункту нам важливо, що маємо 10 білих кульок з 20, а потрібно вибрати 3.
Першу кульку можна вибрати 10 способами з 20, тому ймовірність вийняти першою білу кульку рівна p1=10/20. Після цього залишиться 9 білих кульок з 19, тобто ймовірність що друга кулька буде білого кольору рівна p2=9/19. І останню, третю можна вибрати з ймовірністю p3=8/18.
За правилом сумування ймовірностей нам потрібно знайти їх добуток
p=p1*p2*p3=10/20*9/19*8/18=2/19=0,10526.
б) Одну білу (з 10) і дві чорні (з 6) при 20 кульках можна вибрати з ймовірністю
p=10/20*6/19*5/18=5/144=0,04386.
При цьому неважливо чи білу кульку вибираємо першою чи другою, чи третьою. Якщо поглянути на формулу, то поміняються місцями лише чисельники. Загалом ймовірність від цього не поміняється.
в) Враховуючи, що від порядку входження добуток ймовірностей не змінюється знаходимо значення для третього випадку
p=10/20*6/19*4/18=2/57=0,3509.
Останній метод можете застосовувати для контролю правильності обчислень за формулами теорії ймовірності.
Завдання 2 Для обслуговування деякого будівництва виділено 5 автомобілів. За однакових і незалежних умов з ймовірністю 0,8 вони прибувають на будівництво. Знайти ймовірність того, що в даний момент будівництво обслуговують
- а) всі п'ять автомобілів;
- б) не менше трьох;
- в) жодний автомобіль не прибув на обслуговування.
Розв'язання: Нехай pi=0,8 - ймовірність того, що і-й автомобіль прибув на будівництво, тоді qi=1-pi=1-0,8=0,2 - ймовірність того, що автомобіль не прибув (i=1,2,3,4,5).
а) Ймовірність того, що всі п'ять автомобілів прибули на будівництво
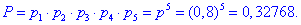
б) Ймовірність того, що не менше трьох автомобілів прибули на будівництво означає або 3, або 4, або 5.
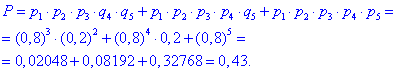
На перший погляд все логічно, але насправді - не зовсім так.
Машини різні, тоді виходить, що важливо які саме дві не приїхали в першому випадку, і яка одна в другому.
А з формули слідує, що 4-та і 5-та не приїхали в першому випадку, та 5 - в другому.
А могли не приїхати 1 і 3, або 2 і 4, і т.д в першому випадку та одна з 5 машин в другому випадку.
Тому в наведеній вище формулі перший доданок слід домножити на С52=10, а другий на С51=5.
Тоді ймовірність рівна
P=10*0,02048+5*0,08192+0,32768=0,94208.
Уважно перегляньте, та обдумайте чому саме так.
в) Ймовірність того, що жодний автомобіль не прибув на будівництво знаходимо за формулою 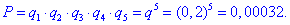
На цьому завдання розв'язано.
Завдання 3 На трьох лініях заводу залізобетонних виробів при однакових і незалежних умовах виготовляються конструкції однієї назви, причому: перша лінія випускає 60%, друга – 30%, третя – 10% всіх виробів. Ймовірність, що кожна конструкція є небракованою відповідно для першої лінії 0,8, для другої – 0,7, для третьої – 0,4.
Знайти ймовірність, якщо
- а) конструкція, що знаходиться під навантаженням, є небракованою;
- б) за умови, що вона небракована, знайти ймовірність того, що її виготовлено на третій лінії.
Розв'язання: Задача на формулу повної ймовірності та Байєса. Нехай Hi - гіпотези, що виріб виготовлений і-м робітником, де i=1,2,3. Тоді ймовірність кожної з гіпотез рівна частці продукції в загальній кількості:
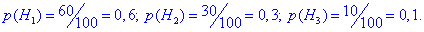
Їх сума рівна повній ймовірності, тобто одиниці. Нехай подія A полягає в тому, що взята навмання конструкція є небракована. Тоді на основі умови можемо виписати ймовірності того, що небраковану конструкцію виготовлено на кожній лінії:
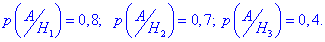
а) За формулою повної ймовірності знаходимо ймовірність, що конструкція, що знаходиться під навантаженням, є небракованою:
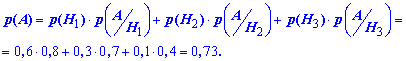
б) Ймовірність того, що конструкцію виготовлено на третій лінії рівна вкладу третього доданку в попередній формулі. Якщо записати це формулами ймовірності, то отримаємо
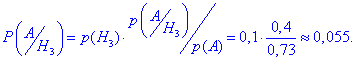
Подібних прикладів на ймовірність Байєса можна навести безліч. На контрольній чи індивідуальній вони є поширені, тому запам'ятайте формули.
Завдання 4 Монету кинуто 100 разів. Знайти ймовірність того, що герб випаде:
- а) 60 разів;
- б) не менше 40 і не більше 90.
Розв'язання: а) Оскільки ймовірність не залежить від історії (попередніх дослідів): p=0,5, то за формулою Бернуллі (дає точне значення) знаходимо
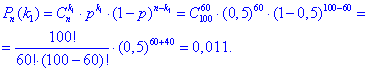
Однак для таких великих факторіалів слід виконувати обчислення в математичному пакеті – Maple, Mathematica, MathCad. Наближене значення ймовірності дає локальна теорема Лапласа.
Оскільки 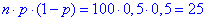 , то похибка формул мінімальна
, то похибка формул мінімальна
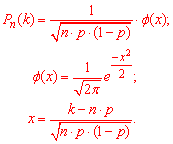 Виконаємо обчислення:
Виконаємо обчислення: 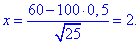
За таблицями табулювання локальної функції Лапласа маємо 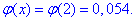
Ймовірність рівна
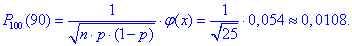
Як бачимо, розбіжність зі значенням отриманим за формулою Бернуллі незначне!
б) Ймовірність, що не менше 40 і не більше 90 разів випаде герб знайдемо за інтегральною формулою Лапласа:
 де
де 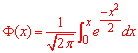 - інтегральна функція Лапласа;
- інтегральна функція Лапласа;
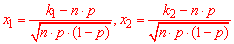 - аргументи інтегральної функції розподілу.
- аргументи інтегральної функції розподілу.
Знайдемо точки
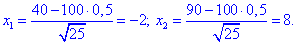
Отож ймовірність рівна 0,977.
На цьому обчислення завершено.
Завдання 5 Монету кинуто чотири рази (n=4). X - число появ герба. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення 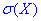 , функцію розподілу F(X) та побудувати її графік.
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=0,5 і q=1-0,5=0,5), то ймовірність випадання герба змінюється за біноміальним законом:
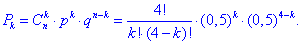
Результати запишемо в таблицю:
 Графік закону розподілу має вигляд
Графік закону розподілу має вигляд
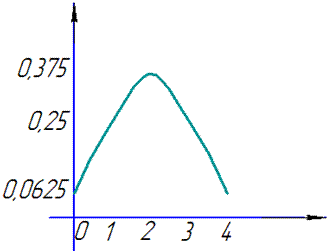
Математичне сподівання випадкової величини
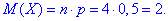
Знаходимо дисперсію
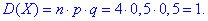
Середнє квадратичне відхилення випадкової величини X:
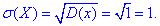
Функцію розподілу випадкової величини X знайдемо за формулою:
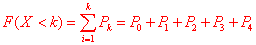
Результати запишемо в таблицю:

Графік функції розподілу має вигляд
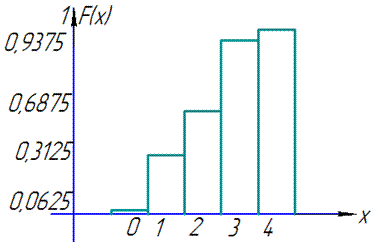
Завдання 6 Випадкова величина задана щільністю розподілу f(x):
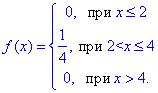
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (2,5;3). Побудувати графіки f(x) та F(x).
Розв'язання: Ітегруванням знаходимо функція розподілу:
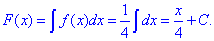
Графік функції f(x) та F(x) (при C=0):
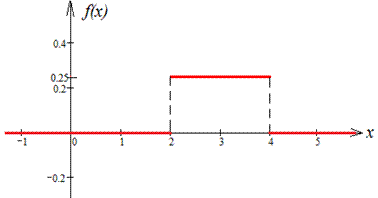
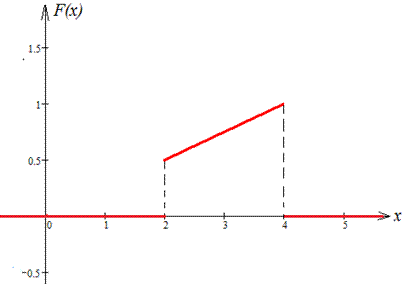
Через інтеграл знаходимо математичне сподівання:
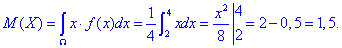
Далі дисперсію:
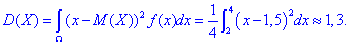
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (2,5;3) знаходимо інтегруванням:
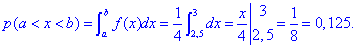
Ось так потрібно пояснювати подібні задачі.
Завдання 7 Відомі математичне сподівання a=1 та середнє квадратичне відхилення 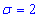 випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
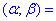 (0;4);
(0;4); - б) абсолютна величина відхилення |x-a| буде менше за 5 (
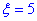 ).
).
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 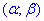 скористаємось формулою Лапласа:
скористаємось формулою Лапласа:
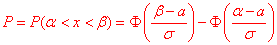 Де
Де 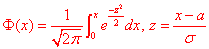 - інтегральна функція Лапласа (її значення є в таблиці).
- інтегральна функція Лапласа (її значення є в таблиці).
Виконуємо обчислення ймовірності
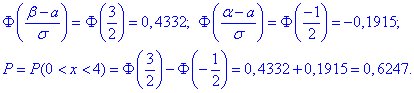
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a| <5 буде менше за 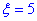 скористаємось формулою:
скористаємось формулою:
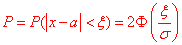
Знаходимо складову
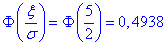
та обчислюємо ймовірність
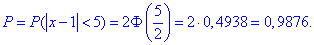
Після таких пояснень до контрольної чи індивідуальної роботи у викладачів не залишиться до Вас ніяких зауважень. Тож вчіть методику знаходження ймовірності в кожному з випадків та застосовуйте знання на практиці.
ВАРІАНТ – 5
Завдання 1. В бригаді 20 робітників, серед яких 11 дівчат, решта хлопці. На нараду послали 4-х представників від бригади. Знайти ймовірність того, що серед них:
- а) одні чоловіки;
- б) одні жінки;
- в) дві жінки і 2 чоловіка.
Розв'язання: Число всіх можливих подій – кількість способів, за якими можна вибрати чоирьох представників з 20 осіб:
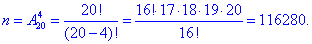
а) Число сприятливих подій – кількість способів, за якими можна вибрати 4-х хлопців із 9 можливих:
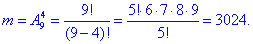
Ймовірність події A, при якій на нараду відправляють 4-х хлопців:
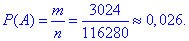
б) Число сприятливих подій – кількість способів, за якими можна вибрати чотирьох дівчат із 11 можливих:
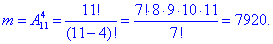
Ймовірність події B, при якій на нараду відправляють чотирьох дівчат:
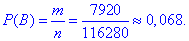
в) Число сприятливих подій – кількість способів, за якими можна вибрати 2-х жінок з 11 і 2-х чоловіків з 9:
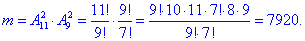
Ймовірність події C, при якій на нараду відправляють 2-х жінок і 2-х чоловіків:
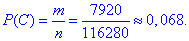
Відповіді можна знайти і геометричним способом. Покажемо, як його реалізувати на практиці.
а) ймовірність, що першим вибрали когось з чоловіків рівна p1=9/20, оскільки маємо 9 чоловік серед 20. Після того, як одного вибрали матимемо 8 чоловіків серед 19, що залишилися. Таким чином, ймовірність що другим виберуть чоловіка рівна p2=8/19. Третього - p3=7/18, та четвертого p4=6/17. За правилом сумування ймовірностей знаходимо їх добуток
P(A)=9/20*8/19*7/18*6/17=42/1615=0,026.
б) Виконавши подібні міркування, прийдемо до ймовірності
P(B)=11/20*10/19*9/18*8/17=22/323=0,068.
в) Дві жінки і два чоловіки можна вибирати кількома способами - ЧЧЖЖ, ЧЖЧЖ, ЖЖЧЧ, ЖЧЧЖ,..
Ймовірність при цьому не зміниться, оскільки знаменник спадає на одиницю з кожним новим добутком, а в чисельнику множники змінюються місцями. Для прикладу, остання записана комбінація матиме ймовірність
P(С)=11/20*9/19*8/18*10/17=22/323=0,068.
Якщо викладачі вимагають користуватися формулами ймовірності - використовуйте перший спосіб, другий в решті випадків (для перевірки).
Завдання 2. Троє студентів складають іспит. Ймовірність, що 1-й студент складе іспит дорівнює 0,8, 2-й – 0,7, 3-й – 0,4. Обчислити ймовірність того, що не складуть іспит:
- а) всі студенти;
- б) тільки один;
- в) хоча б один.
Розв'язання: Нехай p1=0,8, p2=0,7, p3=0,4 - ймовірність того, що іспит складуть відповідно 1-й, 2-й і 3-й студент, тоді для протилежної події q1=1-p1=0,2, q2=1-p2=0,3, q3=1-p3=0,6 - ймовірністі того, що іспит не складуть відповідно 1-й, 2-й і 3-й студенти.
а) Ймовірність того, що іспит не складуть всі студенти рівна добутку:
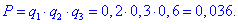
б) Ймовірність того, що іспит не складе тільки один студент рівна трьом варіантам з "або":
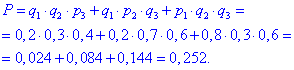
Якщо розписати словами, то або третій або другий або перший студент складе іспит з усіх.
в) Ймовірність того, що іспит не складе хоча б один студент є протилежною подією, що іспит не складуть усі студенти:
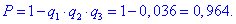
Це найпростіший варіант, оскільки в іншому випадку потрібно сумувати багато ймовірностей з умовою "або". Для перевірки можете переконатися, що довший за часом варіант розрахунків дає такий самий результат.
Завдання 3. На складі в трьох ящиках знаходяться деталі для ремонту автомобілів. Відомо, що в першому ящику 50 деталей, з яких 6 бракованих, у другому – 30 деталей, з яких 5 бракованих, у третьому – 40 деталей, з яких 6 бракованих. Майстер навмання вибирає деталь з будь-якого ящика. Знайти ймовірність того, що взята деталь бракована, й того, що майстер взяв її з другого ящика.
Розв'язання: Задача на застосування формули повної ймовірності та Байєса. В першому ящику 12% бракованих деталей, в другому – 16,67%, в третьому – 15% бракованих. Нехай Hi - гіпотези, що виріб виготовлений і-м робітником, де i=1,2,3. Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності:
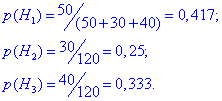
Їх сума рівна повній ймовірності =1. Нехай подія A полягає в тому, що взята навмання деталь бракована. Тоді на основі умови можемо виписати ймовірності того, що браковану деталь взято з кожного ящика:
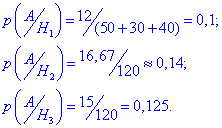
За формулою повної ймовірності знаходимо ймовірність, що деталь бракована:
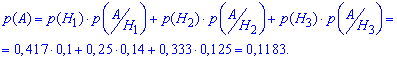
Ймовірність того, що бракована деталь взята з другого ящика за формулою Байєса рівна
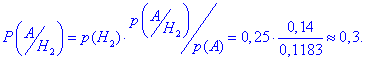
Це фактично вклад другого доданку в попередній сумі.
Завдання 4. Ймовірність народження хлопчика дорівнює 0,51. Знайти ймовірність того, що серед 100 народжених:
- а) рівно 50 хлопчиків;
- б) не менше 30 і не більше 70.
Розв'язання: а) Оскільки ймовірність не залежить від історії (попередніх дослідів), то за формулою Бернуллі знаходимо
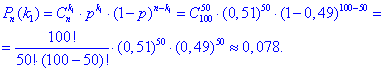
Значення розраховане в математичному пакеті Mathematica.
Наближене значення ймовірності дає локальна теорема Лапласа. Оскільки число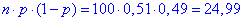 достатнє для застосування формули, то її похибка мінімальна
достатнє для застосування формули, то її похибка мінімальна
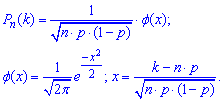
Виконаємо обчислення:
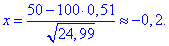
За таблицями табулювання локальної функції Лапласа маємо 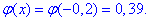
Ймовірність рівна
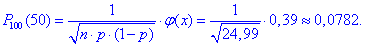
Як можете переконатися, відхилення від значення отриманого за формулою Бернуллі мале!
б) Ймовірність, що народилось від 30 і до 70 хлопців знайдемо за інтегральною формулою Лапласа:
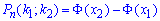
де 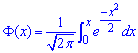 - інтегральна функція Лапласа;
- інтегральна функція Лапласа;
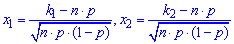 - аргументи інтегральної функції розподілу.
- аргументи інтегральної функції розподілу.
Знайдемо точки
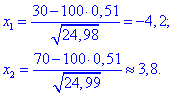
Отож ймовірність вірна
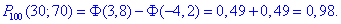
Завдання 5. В білеті чотири запитання (n=4). З ймовірністю 0,4 студент правильно відповідає на кожне з них. X - число правильних відповідей студента. Знайти закон розподілу випадкової величини X, знайти математичне сподівання випадкової величини M(X), дисперсію D(X), середньоквадратичне відхилення 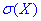 , функцію розподілу F(X) та побудувати її графік.
, функцію розподілу F(X) та побудувати її графік.
Розв'язання: Оскільки від досліду до досліду ймовірність залишається сталою (а саме p=0,4 і q=1-p=0,6), то ймовірність відповідати правильно на запитання змінюється за біноміальним законом:
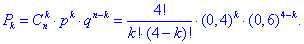
Результати запишемо в таблицю розподілу ймовірностей:
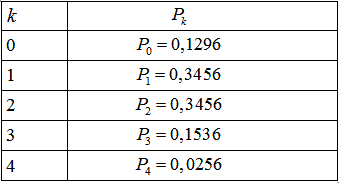
Графік закону розподілу має вигляд
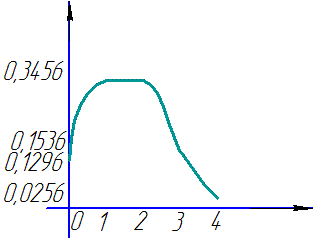 Математичне сподівання випадкової величини
Математичне сподівання випадкової величини
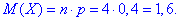
Дисперсія
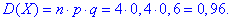
Середнє квадратичне відхилення випадкової величини X:
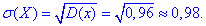
Функцію розподілу випадкової величини X знайдемо за формулою:
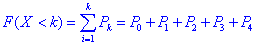
Результати запишемо в таблицю:
 Графік функції розподілу має вигляд
Графік функції розподілу має вигляд
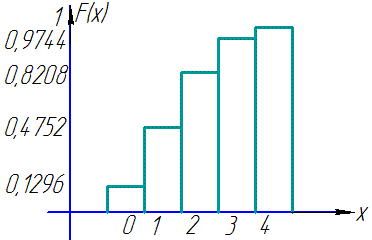
Обчислення не складні і формули під силу вивчити кожному.
Завдання 6. Випадкова величина задана щільністю розподілу f(x):
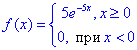
Знайти функцію розподілу F(X), математичне сподівання випадкової величини M(X), дисперсію D(X) випадкової величини та ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b). Побудувати графіки f(x) та F(x).
Розв'язання: Функція розподілу:
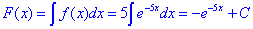
Графік функції f(x) та F(x) (при C=0):
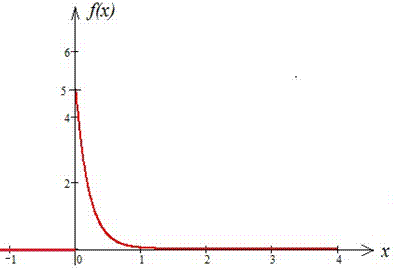
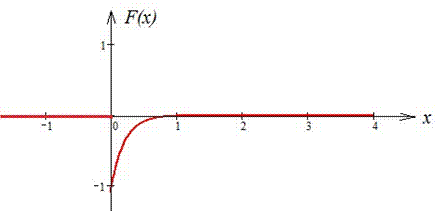
Математичне сподівання:
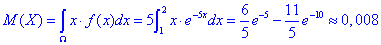
Дисперсія:
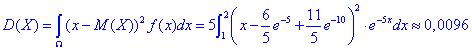
Ймовірність того, що в результаті випробувань x набуде значень, що належать інтервалу (a;b): 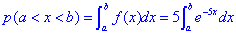
Завдання 7 Відомі математичне сподівання a=5 та середнє квадратичне відхилення 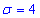 випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
випадкової величини x, яка розподілена нормально. Обчислити ймовірність того, що
- а) ця випадкова величина прийме значення, які належать інтервалу
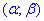 =(0;6);
=(0;6); - б) абсолютна величина відхилення |x-a|<9 буде менше за
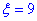 .
.
Розв'язання: а) Для знаходження імовірності того, що випадкова величина x прийме значення, які належать інтервалу 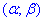 скористаємось формулою:
скористаємось формулою:
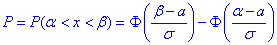
де 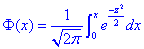 - інтегральна функція Лапласа (її значення є в таблиці).
- інтегральна функція Лапласа (її значення є в таблиці).
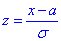 - заміна змінних.
- заміна змінних.
Отож, маємо
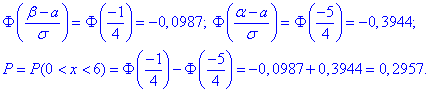
б) Для знаходження імовірності того, що абсолютна величина відхилення |x-a|<9 буде менше за 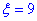 скористаємось формулою:
скористаємось формулою:
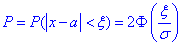
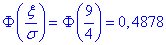
тому ймовірність
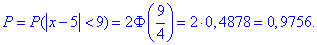
Попереду Вас чекає безліч готових відповідей з контрольних та індивідуальних робіт з теорії ймовірностей.
]]>