В добавку до попередньої статті в якій розглянуті відповіді до трьох завдань на сполучення з кульок наведемо ще 2, які ми отримали від Вас через форму замовлень. Хто вже знайомий з методикою може не читати всіх коментарів, а лише перебігти по умовах завдань та формулах, щоб знайти потрібний матеріал. Хто читає перший раз - звертайте увагу на всі дрібниці, що містяться по обидві сторони відповідей.
Готових відповідей в інтернеті мало, пояснення до більшості матеріалу, що Ви зустрічали теж скупі.
Тому користуйтеся наведеними схемами, діліться посиланням з друзями та перегляньте інші теми з математичних дисциплін.
Приклад 4 В урні a=18 білих і b=14 чорних кульок. З урни навмання виймають c=10 кульок. Знайти ймовірність того, що серед них будуть:
- а) l=3 білі кульки;
- б) s=8 чорних кульок;
- в) l=3 білих або s=8 чорних кульок;
- г) m=8 білих і n=2 чорні кульки;
- д) не більше ніж l=3 білі кульки;
- е) не менше ніж s=8 чорних кульок;
- є) хоча б одну білу кульку;
- ж) кульки одного кольору.
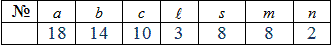
Розв'язання: Класична формула ймовірності p=m/n, де m число сприятливих подій, n - число всіх можливих подій.
а) Число всіх можливих подій знаходимо через сполучення, за якими можна вибрати 10 кульок із 32 (18+14). Порядок входження не важливий, тому застосовуємо формулу
n=C3210 =64512240.
Число сприятливих подій знаходимо через добуток:
m=C183·C147=2800512
де C183 - кількість всеможливих способів, за якими можна вибрати 3 білих кульок з 18;
C147- кількість варіантів вибрати 7 чорних кульок з 14.
Імовірність події A, при якій виймають 3 з 10 кульки білого кольору:
P(A)=m/n= 0.04341055279.
Значення знайдене в математичному пакеті Мейпл. Детальна інструкція, як обчислювати ймовірності в Мейплі наведено в попередній статті. Відповіді можете перевірити калькулятором або за допомогою програм, які вивчаєте у ВУЗах.
б) Число всіх можливих подій вибрати 10 кульок із 32 (18+14) однакове в даному завданні для усіх пунктів і рівне
n=C3210
Число сприятливих подій вибрати 8 чорних ульок з 10 знаходимо з добутку:
m=C148·C182=459459,
де C148 - кількість способів, за якими можна вибрати 8 чорних кульок з 14;
C182- кількість способів, за якими можна вибрати 2 білі кульки з 18.
Імовірність події B рівна:
p(B)=m/n= 0.0071.
в) Ймовірність вибрати 3 білих або 8 чорних кульок з 10 – це сума знайдених p(A) і p(B):
p=p(A)+p(B)=0.043410+0.0071=0,0505.
г) Імовірність вибрати 8 білих і 2 чорних кульки з 10 обчисюємо з формули добутку сполучень:
p(C)=m/n=C188·C142 /C3210=0.0617
тут C188- кількість варіантів вибрати 8 білих кульок з 18;
C142- відповідно всі способи дістати 2 чорні кульки з 14.
д) Імовірність вибрати не більше ніж 3 білі кульки означає або 0, або 1, або 2, або 3.
Це за теорією рівне сумі ймовірностей p(0), p(1), p(2), p(3) :
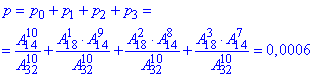
е) Імовірність вибрати не менше ніж 8 чорних кульок означає або 8, або 9, або 10.
Знаходимо суму значень p(8), p(9), p(10):
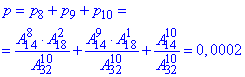
є) Наступний пункт надзвичайно важливий в плані економії Вашого часу при розрахунах.
Читайте уважно - імовірність вибрати хоча б одну білу кульку є протилежною до події вибрати 10 кульок чорного кольору, тому:
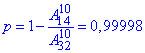
ж) Останій пукт: імовірність вибрати кульки одного кольору означає дістати або 10 з 18 білих кульок, або 10 з 14 чорних кульок:
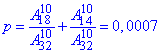
Приклад 5В урні a білих і b чорних кульок. З урни навмання виймають c кульок. Знайти ймовірність того, що серед них будуть:
- а) l білих кульок;
- б) s чорних кульок;
- в) l білих або s чорних кульок;
- г) m білих і n чорних кульок;
- д) не більше ніж l білих кульок;
- е) не менше ніж s чорних кульок;
- є) хоча б одна біла кулька;
- ж) кульки одного кольору.
Зачення параметрів наведені в таблиці
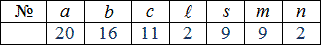
Я правило викладачі мають заготовки подібних приладів та готові відповіді, визначені в МатКаді чи іншій мат. програмі. Задавши такої структури приклад викладач може перевірити групу студентів на знання кількох тем теорії ймовірностей.
Розв'язання:
а) Знаходимо знаменник в формулі ймовірностей – кількість способів, за якими можна вибрати 11 кульок із 36 (20+16)
n=C3611 =36!/11!/(36-11)!.
Далі визначаємо число сприятливих подій через добуток сполучень:
m=C202·C169=21736000,
де C202 - кількість способів, за якими можна вибрати 2 білих кульок з 20;
C169- кількість способів, за якими можна вибрати 9 чорних кульок з 16.
Всюди присутні факторіали, формули не важкі дя школяра, вже не кажучи про студентів.
Імовірність події A, при якій виймають 2 з 11 кульок білого кольору рівна частці: 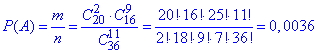
б) Число сприятливих подій дістати 9 кульок з 11 рівна значенню, яке без калькулятора не варто шукати:
m=C202·C169=21736000,
Значення випадково співпадає із знайденим в пункті а).
Для успішного проходження практикуму вартує використовувати інженерні калькулятори, а ще краще ноутбуки чи стаціонарні компютери з самими простими математичними пакетами.
Всі зацікавлені в таких розрахунках можуть почитати в попередній статті, насільки просто знайти ймовірності в Мейплі.
Імовірність події B – вийняти 9 кульок чорного кольору з 11 рівна 0.0036:
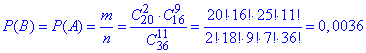
в) Імовірність вибрати 2 білих або 9 чорних кульок з 11 дорівнює сумі p(A) і p(B):
p=p(A)+p(B)=0.0036+0.0036=0,0072.
г) Імовірність вибрати рівно 9 білих і 2 чорні кульок з 11 рівна 0,0335:
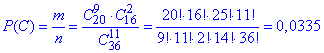
тут C209 - кількість варіантів вибрати 9 білих кульок з 20;
C162- кількість способів дістати 2 чорні кульки з 16.
д) Імовірність вибрати не більше ніж 2 білі кульки означає або 0, або 1, або 2 з 11.
Це сума значень p(0), p(1), p(2) , яка на основі подальшої формули рівна 0.0039: 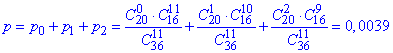
е) Імовірність вибрати не менше ніж 9 чорних кульок можна розуміти як 9, або 10, або 11 з 11.
Це дорівнює сумі значень p(9), p(10), p(11)
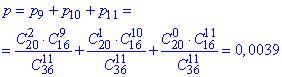
Вона рівна попередньому д) значенню, оскіьки маємо нормаьний розподіл.
Звідси крайні значення рівні, відповідно сума перших трьох як і останніх трьох значень в розкладі рівна.
є) Імовірність вибрати хоча б одну білу кульку є протилежною подією до події - вибрати 11 кульок чорного кольору, тому за правилом повної ймовірності отримаємо:
p=1-C1611/C3611=0.9999905.
Запам'ятайте добре цей випадок. Він найоптимальніший та еономить час на контрольній чи тестах.
ж) Останній пунт, що полягає у виборі кульок одного кольору означає вибір або 11 з 20 білих кульок, або 11 з 16 чорних кульок, тому тут правильну відповідь знаходимо через суму ймовірностей:
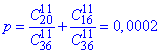
Ще одна серія завдань розв'язана та основні моменти в обчисленнях пояснені.
Не бійтеся експериментувати, користуватися математичними пакетами, задавати викладачам нестандартні питання.
Без бажання докопатися до істини Ви ніколи не опануєте складної теми, тому вчіться і ще раз вчіться!


