Схема Бернуллі виникає при повторних незалежних випробуваннях. Незалежними випробуваннями називаються такі, що не залежать один від одного, і від результатів попередніх випробувань. Вони можуть проводитися як в однотипних умовах, так і в різних. У першому випадку ймовірність появи якоїсь події A у всіх випробуваннях одна і та ж, у другому випадку - міняється від досліду до досліду.
Нехай для кожного досліду імовірність появи події A постійна P(A)=p, ймовірність протилежної події визначається залежністю
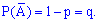 Потрібно знайти ймовірність появи події A рівно m раз в серії із n випробувань. При цьому варто зазначити, що подія A в серії дослідів може чергуватися любим способом, головне щоб виконалася рівно m раз.
Потрібно знайти ймовірність появи події A рівно m раз в серії із n випробувань. При цьому варто зазначити, що подія A в серії дослідів може чергуватися любим способом, головне щоб виконалася рівно m раз.
Результати випробувань для зручності позначаємо літерою A у випадку появи події і "А спряжене"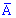 для протилежної.
для протилежної.
Випробування в яких A відбувається m раз, і не відбувається (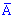 ) n-m за означенням будуть сприятливими. Їх кількість N рівна кількості способів вибору m елементів із n і визначається за формулою сполучень
) n-m за означенням будуть сприятливими. Їх кількість N рівна кількості способів вибору m елементів із n і визначається за формулою сполучень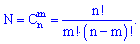 Визначимо імовірність сприятливої комбінації (в серії з n випробувань появи події A рівно m раз). Для простоти запису розглянемо випадок коли подія A відбулася в перших дослідах і не відбулася в решта n-m. Схематично її можна позначити наступним чином, при цьому ймовірність визначити за теоремою множення ймовірностей
Визначимо імовірність сприятливої комбінації (в серії з n випробувань появи події A рівно m раз). Для простоти запису розглянемо випадок коли подія A відбулася в перших дослідах і не відбулася в решта n-m. Схематично її можна позначити наступним чином, при цьому ймовірність визначити за теоремою множення ймовірностей Для інших сприятливих випробувань Pi ймовірність буде така ж, тільки порядок їх в серії з експериментів буде змінюватися
Для інших сприятливих випробувань Pi ймовірність буде така ж, тільки порядок їх в серії з експериментів буде змінюватися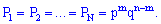 Всі сприятливі випробування є попарно несумісними, тому для знаходження шуканої ймовірності їх потрібно просумувати
Всі сприятливі випробування є попарно несумісними, тому для знаходження шуканої ймовірності їх потрібно просумувати або
або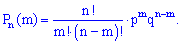
Вивів її вперше швейцарський математик Якоб Бернуллі (1654 р.–1705 р.), за ним і збереглася назва формули.
Якщо просумувати ймовірність всіх випробувань в яких подія A може відбутися від нуля до 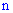 разів в серії із n випробувань то отримаємо повну ймовірність
разів в серії із n випробувань то отримаємо повну ймовірність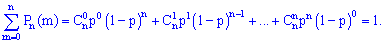 Доданки цієї суми співпадають по вигляду з розкладом бінома Ньютона
Доданки цієї суми співпадають по вигляду з розкладом бінома Ньютона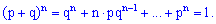 Легко переконатися, що сума рівна одиниці
Легко переконатися, що сума рівна одиниці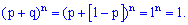 В літературі можна зустріти термін "біноміальний розклад ймовірностей", це якраз множина всіх ймовірностей, яка просумована вище.
В літературі можна зустріти термін "біноміальний розклад ймовірностей", це якраз множина всіх ймовірностей, яка просумована вище.
Як наслідки, з формули Бернуллі виводяться наступні формули для популярних для практики задач:
1) ймовірність появи події A "хоча б один раз" в серії з n випробувань
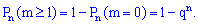
2) ймовірність появи події A "хоча б певну кількість k раз" в серії з n випробувань обчислюють за формулою
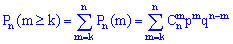
або за властивістю біноміального розкладу ймовірностей
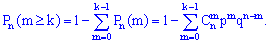
На основі даної залежності вводять в розгляд твірну функцію, яка дає змогу визначити можливу кількість появи події A в серії з n випробувань
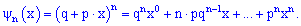
За властивістю твірної функції множники при певному m степені змінної (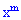 ) дорівнюють імовірності появи події A в серії з n дослідів рівно m раз. Це легко прослідкувати з формули сумування імовірностей всіх можливих випробувань за схемою Бернуллі.
) дорівнюють імовірності появи події A в серії з n дослідів рівно m раз. Це легко прослідкувати з формули сумування імовірностей всіх можливих випробувань за схемою Бернуллі.
Якщо ймовірності появи події в кожному досліді різні P(Ai)=pi, а протилежної 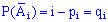 , то за властивостю твірної функції ймовірність події A відбутися m раз в серії n дослідів рівна множнику при xm в розкладі функції за степенями x
, то за властивостю твірної функції ймовірність події A відбутися m раз в серії n дослідів рівна множнику при xm в розкладі функції за степенями x
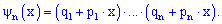
Вона достатньо часто зустрічається при розв'язуванні задач, в яких ймовірності появи події A в кожному наступному досліді змінюються та дозволяє при невеликій кількості m появи події A швидко знайти імовірність (розв'язок задачі).
Найімовірніша число k0 появи події A в схемі Бернуллі лежить в інтервалі
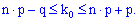
Для застосування схеми Бернуллі потрібно щоб виконувалися три умови:
1) досліди повинні бути незалежні між собою;
2) кожен дослід повинен мати два результати A , протилежна до неї 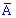 і ніяких інших варіантів;
і ніяких інших варіантів;
3) ймовірність появи події A повинна бути однаковою для кожного наступного досліду.
Розглянемо схему розв'язування типових задач.
Приклад 1. В тирі стрілець проводить 7 пострілів по мішені з ймовірністю улучення кожного 0,8.
Яка ймовірність того, що буде:
а) рівно 4 влучення;
б) не менше за 5 влучень;
в) не більше двох влучань.
Розв'язок. а) проводиться т=7 незалежних одне від одного дослідів з ймовірністю влучення в мішень в кожному з них рівною p=0,8. Ймовірність того, що буде рівно m=4 влучань обчислюємо за формулою Бернуллі:
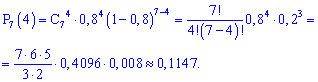
Вона становить p=0,1147.
б) подію A, яка полягає в тому, що при n=7 пострілах буде не менше за 5 влучань можна розглядати як суму трьох несумісних подій: B – 5 влучань з 7, подія C – 6 влучань з 7 і D – всі 7 пострілів влучні.
За формулою Бернуллі знаходимо імовірності подій
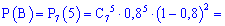
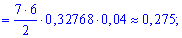
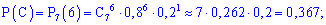
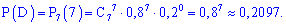
Тоді ймовірність шуканої події A рівна сумі знайдених імовірностей
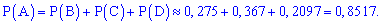
в) Подібним чином ймовірність події A – не більше двох влучань при семи пострілах можна обчислити, як суму ймовірностей трьох подій:
B – 2 влучення з 7,
C – 1 з 7,
D – жодного влучання із 7 пострілів (7 промахів).
На практиці студенти часто забувають розглядати події подібні до жодного влучання D , тож не робіть подібних помилок і Ви, та добре запам'ятайте можливість виникнення такого варіанту. Імовірності знаходимо за знайомою вже формулою
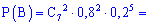
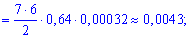
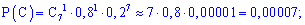
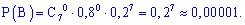
Сумуючи ймовірності одержимо

Однак події A (не більше трьох влучень при п'яти пострілах) і (не менше чотирьох влучень при п'яти пострілах) протилежні один одному, тому
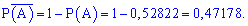
Всі завдання умови виконані і з пояснень є що взяти для кожного з Вас.
Приклад 2. Монету підкидають п'ять разів. Знайти ймовірність того, що герб випаде не більше трьох разів.
Розв'язок. Ймовірність випадання гербу чи решки вважаємо незалежною подією з ймовірністю p=q=0,5. По аналогії з попередньою задачею, шукана ймовірність рівна сумі трьох наступних
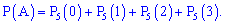
Щоб не шукати стільки доданків, з наведених вище формул отримаємо простішу
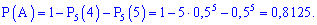
Така ймовірність більша 81%.
Приклад 3. Імовірність появи події в одному досліді рівна 0,4.
Скільки потрібно провести дослідів, щоб найімовірніша кількість появи події була рівна 20.
Розв'язок. Згідно умови виписуємо дані
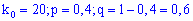
та проводимо розрахунки за нерівністю
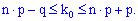
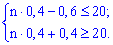
З нерівностей отримаємо
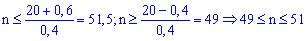
три числа 49,50,51. Отже потрібно провести від 49 до 51 досліду.
Приклад 4. Три біатлоністи незалежно один від одного роблять по одному пострілу в мішень.
Ймовірність попадання в мішень для першого рівна 0,9; для другого – 0,85; для третього – 0,8.
Знайти ймовірність того, що буде закрито дві мішені з трьох.
Розв'язок. Імовірності влучання для стрілків різні, тому застосовуємо твірну функцію.
Для неї вхідні дані приймуть заначення
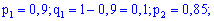
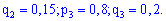
Після підстановки та рокладу в ряд за степенями змінної отримаємо
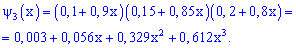
Шукана ймовірність входить в розклад множником при другому степені x2
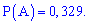
З цього прикладу також легко переконатися, що сума всіх множників при степенях 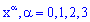 рівна повній ймовірності (одиниці).
рівна повній ймовірності (одиниці).
Задача1. Садівником восени посаджено 80 саджанців яблунь. Ймовірність того, що саджанець навесні оживе, дорівнює 0,8.
Знайти ймовірність того, що тільки 10 саджанців не розпустять листя навесні.
Розв'язання: Найточніше значення ймовірності знайдемо за формулою Бернуллі
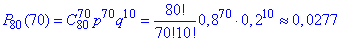
Але при великій кількості незалежних випробувань Ви не зможете скористатися формулою Бернуллі, оскільки калькулятор таких степенів чи факторіалів не обчислить, лише мат. пакети.
Тому для наближених обчислень використовують локальну формулу Лапласа
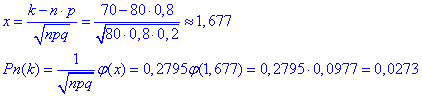
Тут φ(х) значення функції Лапласа.
Порівнянням результатів 0,0277 то 0, 0273, отриманих наведеними способами можете переконатися, що розходження невеликі.
Задача 2. Стрілець здійснює 90 пострілів у мішень. Ймовірність влучення у мішень внаслідок одного пострілу дорівнює 0,82. Знайти ймовірність того, що стрілець влучить у мішень 65 разів.
Розв'язання: Маємо серію n=90 повторних незалежних пострілів, ймовірність влучання в кожному рівна p=0,82, промаху – q=1-0,82=0,18.
Точне значення дає формула Бернуллі
P90(65)=C9065•p65•q(90-65)=90!/(65!•25!)•0,82^65 •0,18^25≈0,007.
Ми як завжди громіздкі обчислення вчимо Вас виконувати в мат. пакетах, зокрема Мейпл комбінації обчислюємо функцією binomial(90,65):
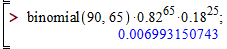
На практиці Вас вчать в таких ситуаціях користуватися локальною теоремою Лапласа, вона дає наближену ймовірність, тому самостійно перевірте розходження в обчисленнях.
Схема Бернуллі на практиці не складна, важливо вловити як в обчисленнях реалізувати завдання типу "не більше m раз", "не менше m раз", "рівно m раз" із n випробувань. Як тільки Ви це зрозумієте, все решта зведеться до сумування, множення та піднесення до степеня.


