Задачі на формулу повної ймовірності та Байєса в плані обчислень одні з найпростіших, головне вловити в яких випадках застосовувати формули.
Далі буде проаналізовано 5 завдань, які внесуть ясність для чого потрібна формула Байєса та який її зміст.
Задача 1 На фабриці виготовляють гвинти. Перша машина виготовляє n1=80%, друга – n1=10%, третя – n1=10% усіх виробів. Частка браку відповідно k1=2%, k2=3%, k3=1%.
а) Яка ймовірність того, що випадково вибраний гвинт бракований?
б) Яка ймовірність того, що його виготовлено 2 - машиною?
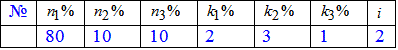
Розв'язання: а) Схема розрахунків спільна для всіх завдань, тому ми один раз її виписуємо, а в наступних прикладах будемо лише посилатися на методику.
Спершу формуємо Hi - гіпотези, що виріб виготовлений і-тій машині, де i=1,2,3.
Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності
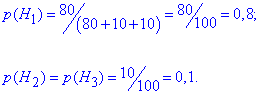
Їх сума рівна повній ймовірності =1. Цю умову обов'язково перевіряйте, інакше теорія не працює, якщо це не підтверджується.
Нехай подія А полягає в тому, що випадково вибраний гвинт бракований. Тут маємо умовну ймовірність, тобто подія має місце якщо попередня умова відбулася (і-та машина вибрана).
Тоді на основі початкових умов можемо виписати ймовірності того, що бракований гвинт виготовлений на кожній з машин
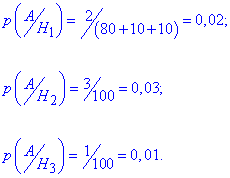
Це фактично значення браку у відсотках розділене на 100%.
За формулою повної ймовірності знаходимо ймовірність, що гвинт бракований
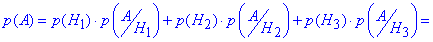
=0.8•0.02+0.1•0.03+0.1•0.03=0.02
Обчислення прості, а суть формули в тому що ймовірність рівна сумі добутків вкладу кожної з машин на відсоток браку.
б) Ймовірність, що бракований гвинт вироблений 2 машиною за формулою Байєса рівна вкладу першої машини в попередню ймовірність
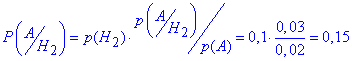Фізична суть цього запису така, що ми знаходимо долю імовірності, що бракована деталь виготовлена 2 машиною у повній ймовірності p(A).
Розглянемо ще кілька завдань для закріплення матеріалу.
Задача 2 На заводі виготовляють запчастини до автомобілів. Перший завод виготовляє n1=70%, другий – n1=20%, третій – n1=10% усіх запчастин. Частка браку відповідно k1=3%, k2=1%, k3=2%.
а) Яка ймовірність того, що випадково вибрана запчастина бракована?
б) Випадково вибрана запчастина виявився бракованою. Яка ймовірність того, що її виготовив 3 станок?
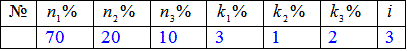
Розв'язання: а) Складаємо Hi - гіпотези, що виріб виготовлений і-тій машині, де i=1,2,3.
Тоді ймовірність кожної з гіпотез рівна частці виробів в загальній сукупності
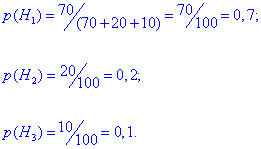
Їх сума рівна повній ймовірності =1.
Подія A полягає в тому, що випадково вибрана запчастина бракована.
Імовірності того, що бракована запчастина виготовлена на одному із заводів рівна відношенні проценту браку до 100%
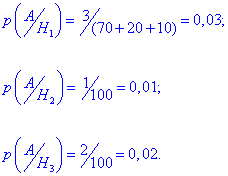
Застосовуючи формулу повної ймовірності знаходимо ймовірність, що деталь бракована
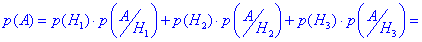
=0.7•0.03+0.2•0.01+0.1•0.02=0.025
б) За формулою Байєса знаходимо імовірність, що бракована запчастина виготовлена на 3 заводі
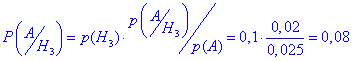
Задача 3 На трьох заводах виготовляють діодні лампочки до фар автомобілів. Перший завод виготовляє n1=70%, другий – n1=12%, третій – n1=18% всієї продукції.
Частка браку відповідно k1=4%, k2=1%, k3=2%.
а) Яка ймовірність того, що випадково вибрана лампочка бракована?
б) Яка ймовірність того, що її виготовлено 3 - заводом?
Розв'язання: а) Складаємо три Hi - гіпотези, що виріб виготовлений заводами.
Імовірність кожної з гіпотез рівна долі лампочок з кожного заводу в загальній кількості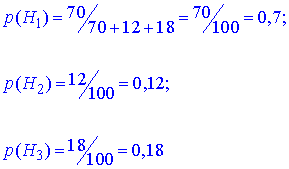 
Сумуванням підтверджуємо, що їх сума рівна повній ймовірності.
Шукана подія полягає в тому, що випадково вибрана лампочка бракована.
На основі початкових умов виписуємо ймовірності того, що бракована лампочка виготовлена кожним із заводів
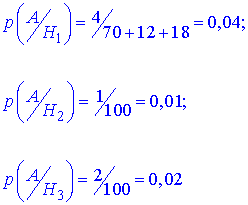
За формулою повної ймовірності знаходимо ймовірність, що вибрана лампочка бракована
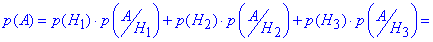
=0.7•0.04+0.12•0.01+0.18•0.02=0.0328
б) Ймовірність, що неробоча лампочка виготовлена на 3 заводі розраховуємо за формулою Байєса
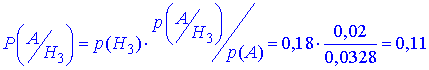
Задача 4 На фабриці виготовляють гвинти. Перша машина виготовляє n1=60%, друга – n1=23%, третя – n1=17% усіх виробів. Частка браку відповідно k1=4%, k2=2%, k3=3%.
а) Яка ймовірність того, що випадково вибраний гвинт бракований?
б) Яка ймовірність того, що його виготовлено 3 - машиною?
Розв'язання: а)Нехай Hi - гіпотези, що виріб виготовлений і-тій машині, де i=1,2,3.
Імовірність кожної з гіпотез рівна долі виробів кожної машини в загальній сукупності
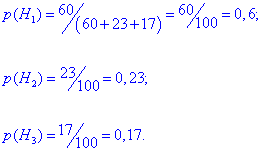
Їх сума рівна повній ймовірності. Подія, що цікавить полягає в тому, що випадково вибраний гвинт бракований.
Виписуємо ймовірності, що бракований гвинт виготовлений кожною з машин
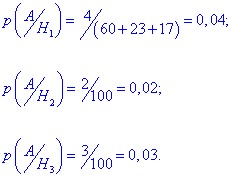
Застосовуючи формулу повної ймовірності знаходимо
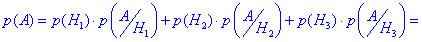
=0.6•0.04+0.23•0.02+0.17•0.03=0.0337
б) За формулою Байєса знаходимо мовірність, що бракований гвинт вироблений 1 машиною
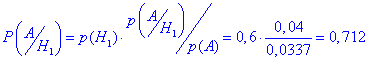
Задача 5 На фабриці виготовляють підошви до взуття. Перша фабрика виготовляє n1=30%, друга – n1=56%, третя – n1=14% усієї продукції.
Відсоток браку на заводах відповідно рівний k1=2%, k2=4%, k3=3%.
а) Яка ймовірність того, що випадково вибрана підошва бракована?
б) Підошва виявилась бракованою. Яка ймовірність того, що її вилито на першій фабриці?
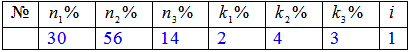
Розв'язання: а) Ймовірність гіпотез, що брак належить певній фабриці рівна
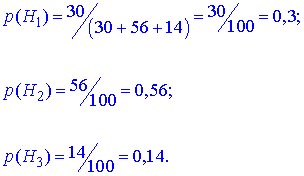
Їх сума рівна повній ймовірності.
Нехай подія A полягає в тому, що випадково вибрана підошва бракована.
Записуємо ймовірності того, що її вилито на фабриці
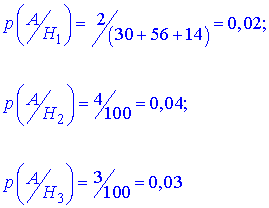
Формула повної ймовірності застосовується щоб знайти p(A), що підошва бракована
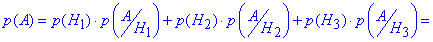
=0.3•0.03+0.56•0.04+0.14•0.03=0.033
б) За формулою Байєса знаходимо імовірність, що браковану підошву виготовлено першою фабрикою
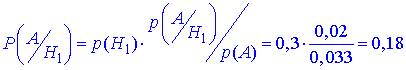
Приклади, що тут розглянуті в основному містять три виробники продукції і шукаємо ймовірність браку. Такі завдання поширені при прийомці і контролі якості продукції.
В інтернеті чимало задач де шукають імовірність позитивних подій.
Наприклад: стрільці стріляють по мішені, відома влучність кожного зі стрільців. Подія полягає в тому, що стрілець влучив. Яка ймовірність, що влучив 2 або 4 стрілець?
Таких задач чимало, а схема розрахунків незмінна і думаю Вам тепер зрозуміла.
Побільше працюйте самостійно та розв'язуйте по кілька завдань на кожну з тем, тоді розуміння предмету та знання прийдуть скоріше та триматимуться голови довший час!
