Якщо кількість незалежних випробувань достатньо велика застосування формули Бернуллі стає трудомістким. Для спрощення обчислень застосовують локальну та інтегральну теореми Лапласа, які дають близький до формули Бернуллі результат при великій кількості випробувань і не потребують великих обчислень.
ЛОКАЛЬНА ТЕОРЕМА ЛАПЛАСА
Ймовірність того, що в n незалежних випробуваннях з ймовірністю появи події A рівній p (0<p<1) подія A наступить рівно k разів (байдуже в якій послідовності) визначається за наближеною формулою
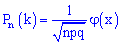
де
 – функція Гауса,
– функція Гауса,
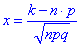 – аргумент функції Гауса;
– аргумент функції Гауса;
q=1-p– ймовірність протилежної події 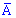 .
.
Формулу Pn(k) називають локальною формулою Лапласа.
Функція phi(x) володіє наступними властивостями:
1) вона є парною функцією phi(-x)=phi(x);
2) для всіх аргументів більших за чотири функція
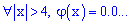
ф(х) менше 2*10^(-3) (двох тисячних) і в більшості практичних розрахунків може прийматися нульовим
Теорему Лапласа рекомендують застосовувати при значеннях добутку більших за дев'ять n*p*q>9.
ІНТЕГРАЛЬНА ТЕОРЕМА МУАВРА-ЛАПЛАСА
Ймовірність, що в n незалежних випробуваннях подія A з імовірністю появи p (0<p<1) настане не менше k1 разів і не більше k2 (незалежно від послідовності появи) наближено визначається залежністю
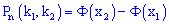
де 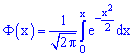 – інтегральна функція Лапласа;
– інтегральна функція Лапласа;
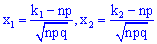 – аргументи інтегральної функції розподілу;
– аргументи інтегральної функції розподілу;
q=1-p – ймовірність не виконання події A.
Функція Лапласа 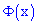 володіє такими властивостями:
володіє такими властивостями:
1) вона є непарною 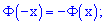
2) для всіх аргументів більших за п'ять вона "відрізняється від 0,5 менше, ніж на 3*10^(-7) 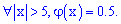
Значення обидвох функцій Лапласа 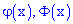 знаходять з таблиць, в яких вони з достатньою точністю протабульовані.
знаходять з таблиць, в яких вони з достатньою точністю протабульовані.
Завдання на застосування теорем Лапласа
Приклад 1. Є 100 лунок по яких випадковим чином розкидають 30 кульок. Кожна кулька з однаковою ймовірністю може попасти в будь-яку лунку (в одну лунку попадає не більше однієї кульки). Знайти ймовірность того, що в вибрану лунку попаде рівно одна кулька.
Розв'язання. Проводиться т=30 незалежних кидків кульок з однаковою ймовірністю попадання при кожному кидку
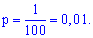
Імовірність попадання в лунку рівно одної кульки визначимо за локальною формулою Лапласа:
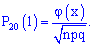
Для цього визначаємо складові
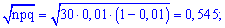
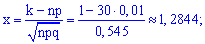
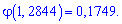
та підставимо в формулу
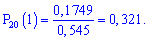
Ймовірність, що попаде лише одна кулька рівна 0,321.
Приклад 2. Проводиться 200 незалежних дослідів з ймовірністю успіху у кожному 24 %. Яка ймовірність успішного проведення 50 дослідів?
Розв'язання. За умовою 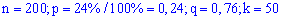 ,знаходимо складові формули Лапласа
,знаходимо складові формули Лапласа
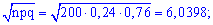
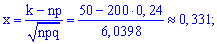
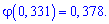
Підставляючи в формулу, знаходимо ймовірність
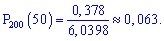
Ймовірність досить мала p=0,063.
Приклад 3. Ймовірність виходу з ладу за зміну одного верстату рівна 0,1. Визначити ймовірність виходу з ладу від 2 до 13 верстатів при наяних 100.
Розв'язання. Записуємо вхідні дані
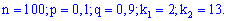
Для подібних прикладів застосовуємо інтегральну формулу Муавра-Лапласа та знаходимо ймовірність
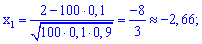

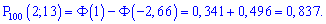
В результаті отримаємо p=0,837/
Розв'язування задач за наведеними теоремами дає змогу при великій кількості випробувань знаходити наближене значення ймовірності. Локальна теорема необхідна при визначенні конкретної кількості появи подій, інтегральна теорема Муавра-Лапласа – у випадках, коли задано діапазон можливої кількості появ події. Таблиці табулювань функцій, які застосовуються у формулах можна знайти в довідниках по теорії ймовірностей та інтернеті.


