При статистичній обробці даних часто знаходження частот варіанти та побудови гістограм частот вибірки та відносних частот буває замало.
Необхідно визначити довірчий інтарвал для вибірки, що характеризується середнім квадратичним відхиленням та вибірковим середнім.
Інтервальні оцінки вибірок є поширеними в статистиці, тому такі завдання Ви повинні навчитися вирішувати.
Особливо це стосується тих студентів які вирішили пов'язати роботу з статистикою, опитуванням, моніторингом і тому подібним.
Надійність як правило лежить в межах 0.95..0.99.
Далі в статті піде мова як знайти довірчий інтеграл?
Як за допомогою інтегральної функції Лапласа знайти значення точки t для формули довірчого інтегралу?
Теорії з цих питань достатньо в інтернеті, проблема полягає на практичних, тому переходимо до аналізу готових відповідей.
Про те де брати таблиці функції Лапласа мова тут не йтиме, як і про її властивості.
Ці завдання вирішені раніше в публікаціях, тому кому цікаво - можете переглянути матеріали.
Приклад 1 Записати довірчий інтервал для оцінки з надійністю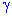 
=0.95 невідомого математичного сподівання a нормально розподіленої ознаки X генеральної сукупності, якщо відомі генеральне середнє квадратичне відхилення 
=6, вибіркове середнє 
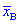=115,24 і об'єм вибірки n=36
Розв'язання: Надійність рівна подвійній інтегральній функції Лапласа, тому з рівняння
Інтегральну функцію Лапласа знаходимо за формулою в математичних пакетах
-
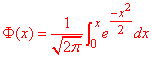або за допомогою таблиць інтегральної функції Лапласа, які легко знайти онлайн.
Таким чином знаходимо точку t
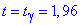
Межі інтервалу довіри шукаємо за формулами:
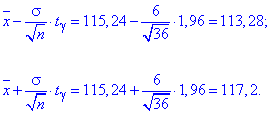
Вони не складні в плані обчислень.
Звідси ознака належить інтервалу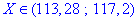 
з надійністю 0.95.
Приклад 2 Записати довірчий інтервал для оцінки з надійністю hamma=0.95 невідомого математичного сподівання a нормально розподіленої ознаки X генеральної сукупності, якщо відомі генеральне середнє квад¬ратичне відхилення sigma=7, вибіркове середнє xB=116,36 і об'єм вибірки n=49.
Розв'язання: З рівняння
за допомогою функції Лапласа t=1,96..
Межі інтервалу довіри шукаємо за формулами:
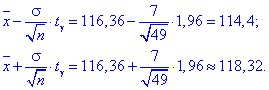
Отже, Xє(114,4; 118,32) з надійністю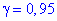 
.
Приклад 3 Записати довірчий інтервал для оцінки з надійністю gamma=0.99 невідомого математичного сподівання a нормально розподіленої ознаки X генеральної сукупності, якщо відомі генеральне середнє квадратичне відхилення sigma=4, вибіркове середнє xB=10,2
і об'єм вибірки n=16.
Розв'язання: З рівняння 
за допомогою функції Лапласа методом інтерполяції знаходимо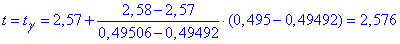 
Межі інтервалу довіри шукаємо за формулами:
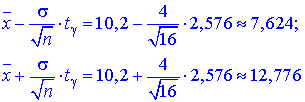
Отже, Xє(7,624; 12,776) з надійністю 0.99.
Приклад 4 Записати довірчий інтервал для оцінки з надійністю hamma=0.99 невідомого математичного сподівання a нормально розподіленої ознаки X генеральної сукупності, якщо відомі генеральне середнє квад¬ратичне відхилення sigma=5, вибіркове середнє xB=16 і об'єм вибірки n=25.
Розв'язання: З рівняння 
за допомогою функції Лапласа методом інтерполяції знаходимо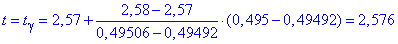 
Межі інтервалу довіри шукаємо за формулами: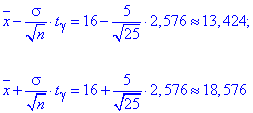 
Отже, Xє(13,424; 18,576) з надійністю 0.99.
Приклад 5 Записати довірчий інтервал для оцінки з надійністю hamma=0.95 невідомого математичного сподівання a нормально розподіленої ознаки X генеральної сукупності, якщо відомі генеральне середнє квадратичне відхилення sigma=4, вибіркове середнє xB=18 і об'єм вибірки n=100.
Розв'язання: З рівняння 
за допомогою функції Лапласа t=1,96.
Межі інтервалу довіри шукаємо за формулами:
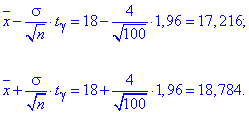
Отже, Xє(17,216; 18,784) з надійністю 0.95.
Приклад 6 Записати довірчий інтервал для оцінки з надійністю hamma=0.95 невідомого математичного сподівання a нормально розподіленої ознаки X генеральної сукупності, якщо відомі генеральне середнє квадратичне відхилення sigma=10, вибіркове середнє xB=110 і об'єм вибірки n=90.
Розв'язання: З рівняння 
за допомогою функції Лапласа t=1,96.. Межі інтервалу довіри шукаємо за формулами:
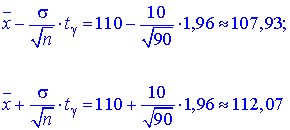
Отже, Xє(107,93; 112,07) з надійністю 0.95 .
Як бачите обчислень не багато, по суті робота більше зводиться до відшукання за значенням функції Лапласа точки якій це значення відповідає.
Всі решта операції на рівні шкільної програми.
