Далі наведена інструкція, як складати рівняння прямої регресії X на Y, та рівняння прямої регресії Y на X за кореляційною таблицею. Такі завдання задають на практикумах з теорії ймовірностей і математичної статистики, скорочено ТІМС. Якщо Ви студент 1, 2 курсу ВУЗу і Вам читають ТІМС, то Вам обов'язково доведеться обчислювати приклади на рівняння лінії регресії, які розв'язують за наступним алгоритмом.
Схема знаходження рівняння прямої лінії регресії X на Y, та Y на X
Завдання 4.3 За даними кореляційної таблиці знайти вибіркове рівняння прямої лінії регресії А) X на Y; Б) Y на X.
Y \ X | -1 | 0 | 1 | 2 |
-2 | 22 | 15 | 0 | 0 |
-1 | 0 | 25 | 15 | 0 |
0 | 0 | 0 | 10 | 13 |
(Результати округлити до тисячних).
Розв'язування: Алгоритм знаходження прямої лінії регресії:
Обчислимо суму всіх елементів (наприклад, по рядках):
n=(22+15)+(25+15)+(10+13)=37+40+23=100.
Знаходимо середнє значення елементів X (значення xi беремо по стовпцях):
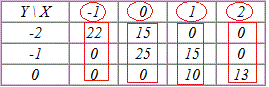
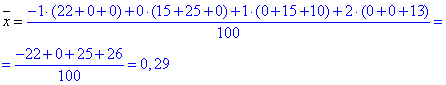
Уважно перегляньте підказки з таблиці та порівняйте з записом з чисельника х.
Середнє значення елементів Y (значення yi беремо по рядках):
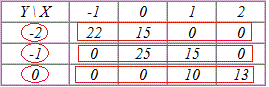
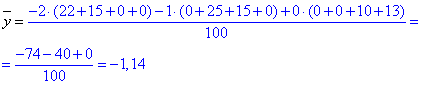
З наведеними підказками Вам легше буде розв'язати приклади на складання рівняння лінії регресії.
Обчислимо середні арифметичні значення величин x^2, y^2 і xy:
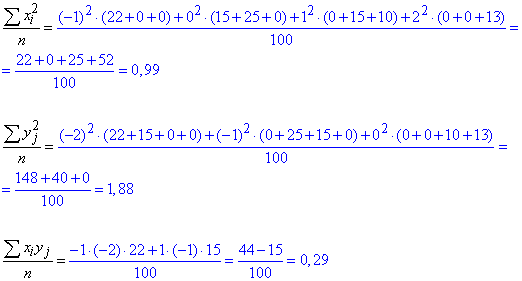
Тут аналогічний до попередніх розрахунків алгоритм, тільки величини xi, yi беремо у квадраті, або знаходимо їх добутки.
(клітинки, в яких стоять нулі не записували).
Обчислимо дисперсії σx, σy та коваріацію Cxy за формулами:
Знайдемо коефіцієнт кореляції за формулою:
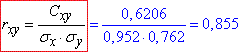
Оскільки добуток модуля коваріації на корінь з кількості елементів більший за трійку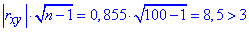 
, то зв'язок достатньо вірогідний.
А) Обчислимо рівняння ліній регресії X на Y за формулою:
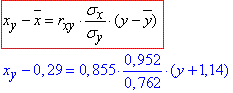
xy=1,069y+1,509.
Б) Складемо рівняння ліній регресії Y на X
yx=0,684x-0,942.
Відповідь:x=1,069y+1,509; y=0,684x-0,942.
Завдання 4.4 За даними кореляційної таблиці знайти вибіркове рівняння прямої лінії регресії А) X на Y; Б) Y на X.
Y \ X | -2 | -1 | 0 | 1 |
-3 | 10 | 0 | 0 | 0 |
-2 | 0 | 12 | 6 | 0 |
0 | 0 | 0 | 12 | 10 |
(Результати округлити до тисячних).
Розв'язування: Порахуємо суму всіх елементів (наприклад, по рядках):
n=10+(12+6)+(12+10)=10+18+22=50.
Середнє значення елементів X (значення xi беремо по стовпцях):
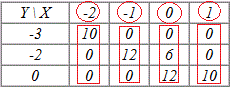
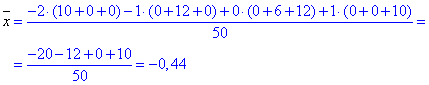
Аналогічні до попереднього завдання підказки, звідки беремо значення для розрахунку середнього значення X.
Визначаємо середнє значення елементів Y (значення yi беремо по рядках):
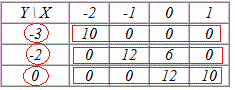
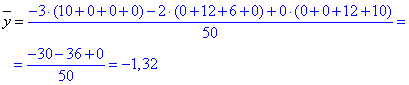
Обчислення не важкі, головне не пропустити ненульові значення таблиці.
Обчислимо середні арифметичні значення величин x^2, y^2 і xy:
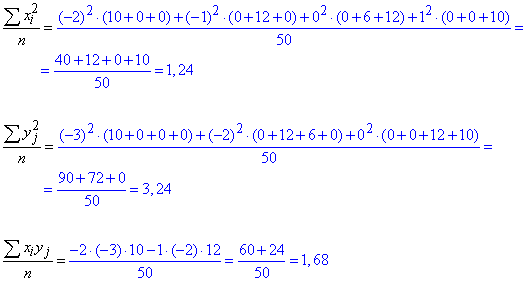
З наведеними обчисленнями у Вас теж не повинно виникнути труднощів.
(клітинки, в яких стоять нулі не записували).
Знайдемо дисперсію σx, σy та коваріацію Cxy за формулами:
Обчислимо коефіцієнт кореляції:
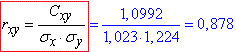
Оскільки вираз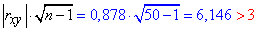 
приймає більше значення за трійку, то зв'язок достатньо вірогідний.
А) Складемо рівняння ліній регресії X на Y за формулою:
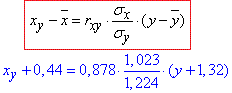
xy=0,734•y+0,529.
Б) Рівняння ліній регресії Y на X знайдемо з формули:
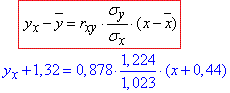
yx=1,051•x-0,858.
Відповідь:x=0,734•y+0,529; y=1,051•x-0,858.
Сподіваюсь, інструкції, як знаходити рівняння прямої лінії регресії будуть корисними Вам в навчанні, та допоможуть на відмнно здати практикум з ТІМС та екзамени.
