Нехай в умовах експерименту подія A з'являється спільно з однією з групи несумісних подій (гіпотез) Hi(i=1,...,n), що утворюють повну групу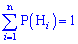 
, відомі або можливо встановити апріорні ймовірністі P(Hi) кожної з гіпотез та умовні ймовірності P(A/Hi) події A за умови, що здійснилася та або інша гіпотеза, тоді ймовірність події A визначається за формулою повної ймовірності:
де P(Hi)– ймовірність гіпотези Hi;
P(A/Hi)– умовна ймовірність події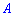 
при виконанні гіпотези Hi. Наведена формула називається формулою повної ймовірності.
Задачі на повну ймовірність
Задача 1. В магазині три холодильники, в яких закінчується морозиво. У першому - 4 білих морозива і 6 шоколадних, у другому - 2 білих і 8 шоколадних, у третьому - 3 білих і 7 шоколадних. Навмання вибирають холодильник і виймають з нього морозиво, визначити ймовірність того, що воно біле.
Розв'язування. Позначимо події наступним чином: Hi – вибрано i-й холодильник, A – вибрано біле морозиво.
Тоді ймовірності витягнути з кожного холодильника однакові і рівні 1/3
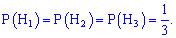
Ймовірності витягнути біле морозиво будуть рівні кількості морозива в кожному з холодильників розділеній на загальну кількість морозива
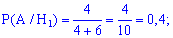
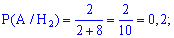
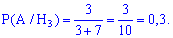
Тут Вам має бути усе зрозуміле.
Використовуючи формулу повної ймовірності, знаходимо
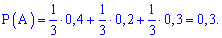
Таким чином ймовірність витягнути біле морозиво рівна 0,3 або 30%.
Задача 2. В офісі є чотири ноутбуки виготовлених компаніює A, 6 компанією B, 8 компаніює C та два, які виготовляє D. Гарантії, що ноутбуки цих компаній працюватимуть протягом гарантійного терміну без ремонту становлять 70 %, 80%, 85%, та 55% для кожної з них. Потрібно знайти ймовірність того, що вибраний ноутбук працюватиме без ремонту протягом гарантійного терміну.
Розв'язування. Позначимо події наступним чином: Hi – вибрано ноутбук компанії;
A – ноутбук працюватиме без ремонту.
Ймовірності вибору ноутбуків кожної з компаній вважаємо рівні їх кількості - на основі цього ймовірності приймуть значення :
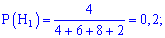
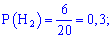
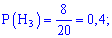
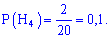
Такі прості обчисення повинен навчитися вионувати та бачити кожен студент.
Ймовірності, що вони працюватимуть без ремонту беремо з умови
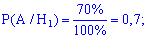
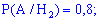
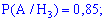
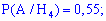
Тут ми просто переводимо проценти в ймовірності.
Застосовуємо формулу повної ймовірності:
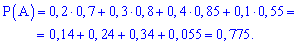
Таким чином, ймовірність безремонтної роботи ноутбука рівна 0,775. Колись це значення можливо було великим досягненням, в теперішній час, якщо б 22,5% ноутбуків потребували ремонту під час гарантійного терміну - це буа б велика проблема виробників.
ФОРМУЛА БАЙЄСА
Нехай гіпотези Hi(i=1,...,n) утворюють повну групу несумісних подій (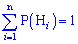
) і нехай подія A відбувається обов'язково з однією з гіпотез Hi. Нехай подія A відбулася, тоді ймовірність того, що вона відбулася саме за умови Hi визначається формулою Байєса:
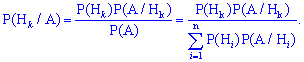
Розглянемо практичну сторону застосування формули Байєса.
Задача 3. Задані умови першої задачі. Потрібно встановити ймовірність того, що морозиво витягнули з другого холодильника.
Розв'язування. Випишемо результати першої задачі, які потрібні для обчислень
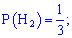
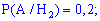
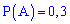
та підставимо у формулу Байєса
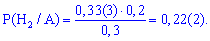
Як можна бачити, такі обчислення не складні, головне зрозуміти, що і як визначається.
Задача 4. Для другої задачі потрібно встановити ймовірності того, що справний ноутбук належить до компаній C та D.
Розв'язування. Випишемо попередньо знайдені ймовірності
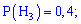
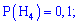
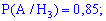
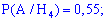
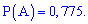
та застосуємо формулу Байєса
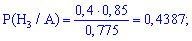
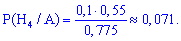
Добре розберіться чому саме так, далі буде важче.
Задача 5. На склад надходять телефони трьох заводів, причому частка телефонів першого заводу становить 25%, другого – 60%, третього – 15%. Відомо також, що середній відсоток телефонів з браком для першої фабрики становить 2%, другої – 4%, третьої – 1%. Знайти ймовірність того, що:
а) навмання взятий телефон виявиться з браком;
б) телефон виготовлений на першому заводі, якщо він бракований;
в) на якому заводі найвірогідніше був виготовлений телефон, якщо він якісно зроблений?
Розв'язування. Проаналізуємо ожне із завдань, щоб Ви якомого краще навчилися розбиратися в формулах.
а) Введемо для ясності позначення:
A – навмання вибраний телефон виявився бракованим;
Припущення: H1 – телефон виготовлений на першій, H2 – другій та H3 – третій фабриках відповідно.
Гіпотези є попарно несумісними і утворюють повну групу. Ймовірність кожного припущення визначаємо діленням процентної частки продукції до всієї (100%)
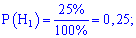
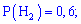
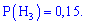
Це не важко знайти для більшості задач теорії ймовірностей..
Подібним чином визначаємо умовні ймовірності шуканої події A
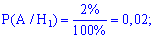
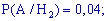
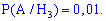
Застосуємо формулу повної ймовірності для визначення можливості вибору бракованого телефону
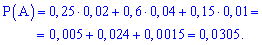
Ймовірність трохи більша за три сотих.
б) для відшукання ймовірності припущення H1 за умови, що подія A виконалася застосуємо формулу Байєса
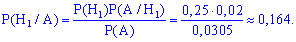
Таким чином, маючи попередні розрахунки, провести обчислення досить просто.
в) щоб визначити, на якому заводі найвірогідніше був виготовлений нормальний телефон, необхідно порівняти між собою ймовірності кожного з припущень :
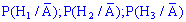
де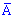 
подія (витягнули телефон без браку) протилежна до події A. Для протилежних подій використовують формулу
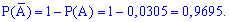
За подібною формулою визначаємо умовні ймовірності події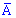 
, за умови що справедливі припущення H1, H2, H3
За формулою Байєса обчислюємо ймовірності
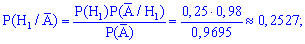
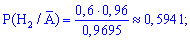
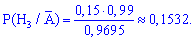
Найбільшу імовірність має друге припущення, тому телефон виготовлено на другому заводі.
Приклад 6. У першій урні 2 білих та 6 чорних куль, у другій – 4 білих та 2 чорних. З першої урни навмання переклали 2 кулі в другу, після чого з другої урни навмання дістали одну кулю.
а) Яка ймовірність того, що ця куля біла?
б) Куля, взята з другої урни, виявилася білою.
Яка ймовірність того, що з першої урни в другу були перекладені 2 білі кулі?
Розв'язування: Результат вибору кульки залежить від того, які кулі переклали.
1) переклали два білі ⇒ у другому кошику стало 6 білих та 2 чорних.
p=6/8 – ймовірність вийняти білу кулю
2) переклали два чорні ⇒ у другому кошику стало 4 білих та 4 чорних.
p=4/8 – ймовірність вийняти білу кулю
3) переклали один білий та один чорний ⇒ у другому кошику стало 5 білих та 3 чорних.
p=5/8 – ймовірність вийняти білу кулю.
Це напряму випливає з того, які набори кульок отримали в другій урні.
Записуємо події - гіпотези:
H1–"переклали дві білих"
H2–"переклали дві чорні"
H3–"переклали чорну, білу"
H4-"переклали білу, чорну".
Ймовірність гіпотез залежить від кількості мячів того чи іншого кольору, тому
p(H1)=2/8*1/7=2/56;
p(H2)=6/8*5/7=30/56;
p(H3)=p(H4)=6/8*2/7=12/56.
Гіпотези утворюють повну групу подій
p(H1)+p(H2)+p(H3)+p(H4)=1.
Подія A-"з другого кошика витягнуто білу кулю":
Випишемо скільки яких куль стало в другій урні та ймовірності події
6 б і 2 ч p(A/H1)=6/8;
4 б і 4 ч p(A/H2)=4/8;
5 б і 3 ч. p(A/H3)=5/8;
5 б і 3 ч p(A/H4)=5/8.
Тоді за формулою повної ймовірності маємо:
p(A)=2/56·6/8+30/56·4/8+12/56·5/8+12/56·5/8=9/16
б) за формулою Байєса знаходимо ймовірність, що взята куля була в другій урні:
p(H2/A)=p(A/H2)*p(H2)/p(A)=30/56·4/8:(9/16)=10/21.
Відповідь: 10/21.
Приклад 7. В спеціалізовану лікарню поступають в середньому 50% з захворюванням А, 30% - В, 20% - С. Ймовірність повного вилікування для А становить 0,7, В - 0,8, С -0,9. Пацієнта виписано здоровим.
Яка ймовірність того, що він хворів В?
Розв'язування: Задача на повну ймовірність та формулу Байєса.
Так як в умові задано захворювання А, В, С, так і позначимо гіпотези.
Тоді їх ймовірності рівні
p(A)=50%/100%=0,5;
p(B)=30%/20%=0,3;
p(C)=20%/100%=0,2.
Тоді ймовірності видужання D за гіпотез рівні:
p(D/A)=0,7;
p(D/B)=0,8;
p(D/C)=0,9.
Знайдемо спершу ймовірність, що пацієнта виписано здоровим:
p(D)=0,5*0,7+0,3*0,8+0,2*0,9=0,77.
Тоді ймовірність, що він хворів В рівна:
p(B/D)=p(D/B)*p(B)/p(D)=0,8*0,3/0,77≈0,31
Відповідь: 0,31.
Задач на знаходження повної ймовірності та застосування формули Байєса в літературі та інтернеті безліч. Варто ввести в гуглі потрібний запит і вам тут же буде запропоновано гори матеріалів до вибору. Тож засвоїти даний матеріал не важко, варто лише уважно (без паніки) розібратися з наведеними прикладами та аналогічні до них. Всі подібні вирішуються за приведеною схемою. Залишайтеся з нами і Ви знатемете більше, ніж розраховували!
