Комбінаторика є важливим розділом математики, що досліджує закономірності розташування, впорядкування, вибору і розподілу елементів з фіксованої множини.
При великому числі можливих наслідків випробування способи прямого перебору можливих варіантів малоефективні. На допомогу приходять комбінаторні методи, в основі яких лежать два настутних правила.
ПРАВИЛО ДОДАВАННЯ
Якщо дві взаємовиключні події можуть бути виконані відповідно k та m способами, тоді якусь одну з цих подій можна виконати k+m способами.
Приклад 1. З міста А в місто В можна добратися 12 потягами, 3 літаками, 23 автобусами. Скількома способами можна добратися з міста А у місто В?
Розв'язання. Проїзд з А у В на потягу, літаку або автобусом є подіями, які не можуть виконуватися одночасно однією людиною (взаємовиключними), тому загальну кількість маршрутів можна обчислити сумуванням способів пересування
N=12+3+23=38.
В цьому і полягає правило додавання.
ПРАВИЛО МНОЖЕННЯ
Нехай дві виконувані одна за одною дії можуть бути здійснені відповідно k та m способами. Тоді обидві вони можуть бути виконані k*m способами.
Приклад 2. У турнірі беруть участь 8 команд з хокею. Скільки існує способів розподілити перше, друге та третє місця?
Розв'язання. Відповідно до умови аналіз призових місць має бути наступним:
перше місце займе одна з 8 команд, друге – одна з 7, третє – одна з 6, оскільки кожна з них не може претендувати одночасно на два призових місця. Тому таких способів буде
N=8*7*6=336
Обидва правила узагальнюються на випадок будь-якої скінченної кількості дій.
У комбінаториці розрізняють три види різних з'єднань (комбінацій) елементів фіксованої множини: перестановки, розміщення, сполучення. Нижче будуть дані їх означення з позначеннями, які найбільшвживані.
Перестановками з m елементів називаються такі їх сукупності, що відрізняються одна від іншої тільки порядком входження елементів. Їх позначають P(m) та визначають за формулою
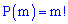
 - факторіал числа m, визначається за правилом
- факторіал числа m, визначається за правилом
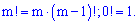
Приклад 3.Скількома способами можна в садочку поставити групу з 15 дітей в ряд?
Розв'язання. На перше місце є можливість поставити когось із 15 дітей, на друге одного з 14 і т.д. Загальна кількість рівна 15 факторіал
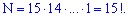
Переглянути приклади на перестановки.
Розміщеннями з n елементів по m називаються такі сукупності m елементів, що відрізняються одна від іншої принаймні одним елементом або порядком їх входження (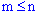 ):
):
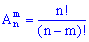
Фомула розміщень не надто складна і доволі часто Ви будете нею ористуватися на практиці, тому рекомендуємо її вивчити.
Приклад 4. Скільки різних трицифрових чисел можна скласти за допомогою цифр від 1 до 9?
Розв'язання Загальна кількість чисел обчислюється за формулою розміщень
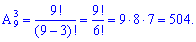
Отримана відповідь Вам і зрозуміла і тривіальна. Переглянути задачі на розміщення.
Сполученнями з n елементів по m називаються такі сукупності m елементів, що відрізняються одна від іншої принаймні одним елементом (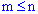 ) :
) :
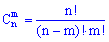
З формули сполучень бачимо, що вони приймають ще менше значення ніж розміщення. З наступного завдання Ви зрозумієте де використовують розміщення.
Приклад 5. Скількома способами можна вибрати три цифри з дев'яти 1, 2, 3,...,9?
Розв'язання. Кількість усіх можливих способів визначаємо з формули
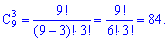
Зверніть увагу на приклади комбінацій (сполучень).
Приклад 6. Студент знає відповіді на 30 із 40 питань програми. На екзамені він отримує білет у якого 10 навмання вибраних питань програми. Яка ймовірність того, що він складе іспит з оцінкою «відмінно», якщо для цього потрібно відповісти не менше, ніж на 9 питань білета?
Розв'язання: Оскільки порядок входження питань в білет не важливий, а тільки має значення чи знає студент відповідь на питання, то слід застосовувати формулу сполучень. Кількість всеможливих способів сформувати білети з 10 питань серед 40 рівна
n=С4010=40!/(10!•30!)=847660528.
Відповісти потрібно на 9 з 10 або всі 10 питань.
1) 9 з 10 означає вибрати 9 питань з 30 на які знає відповіді і 1 з (40-30)=10, на які не знає відповіді, тобто кількість рівна
m1=С309•С101=30!/(9!•21!)•10=143071500.
2) 10 питань в білеті, на які студент знає відповіді з 30 доступних можна сформувати С3010 способами:
m2=С3010=30!/(10!•20!)=30045015.
За правилом додавання ймовірностей кількість способів сформувати білети на які студент знає відповіді не менше ніж на 9 питань з 10 рівна:
m=m1+m2=173116515.
Обчислимо ймовірність здати на відмінно екзамен
p=m/n=0,204.
Приклад 7. З колоди, в якій 36 карт, навмання вибирають 4 карти. Знайти ймовірність того, що серед них буде хоча б три тузи.
Розв'язання: З умови бачимо, що порядок входження тузів в набір з 4 карт нас не цікавить, тобто не важливо чи ми витягнемо туза першим чи останнім.
В такій ситуації слід застосовувати формулу комбінацій Сnk.
Кількість способів вибрати 4 різні карти з 36 рівна
N=С364=36!/(4!•32!)=58905.
Для любителів обчислювати в пакеті меймл за комбінації відповідає binomial(N,m):
N:=binomial(36,4)=58905.
Умова, що буде хоча б три тузи означає або 3 «або» 4 тузи.
На мові ймовірностей «або» означає додавання:
Кількість способів вибрати три тузи з 4 і ще одну карту з решти колоди (36-4)=32 рівна добутку комбінацій
m1=С43•С321=4•32=128.
4 з 4 тузів можна вибрати єдиним способом, тому
m2=C44=1.
За означенням класичної ймовірності обчислюємо частку сприятливих подій до все можливих, тому
p=(m1+m2)/N=129/58905≈0,00219.
Приклад 8. З одинадцяти букв азбуки складено заголовок української казки «КОТИГОРОШОК». Дитина, яка не вміє читати, розсипала букви, а потім зібрала в довільному порядку. Знайти ймовірність того, що вона збере слово «КОТИГОРОШОК».
Розв'язання. На здоровий глузд виглядає, що така ймовірність рівна нулю, ніяка дитина такого довгого слова не складе.Проте в теорії ймовірностей є своя дума з цього приводу і вона поягає в насупному:
з одинадцяти букв можна скласти різні буквосполучення, що відрізняються між собою тільки порядком букв, тому число всіх можливих перестановок рівна 11 факторіа
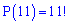
Однак букви «К» і «О» можуть займати одну з чотирьох , та одну з двох позицій відповідно, їх можна переставляти. Тому число сприятливих подій рівне
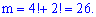
Шукана ймовірність прийме значення
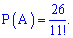
Дане число Вам нічого не говорить, бо Ви не бачите нулів після коми. Запишемо ймовірність десятковим значенням
P(A)=0,00000065...
Це означає, що лише 65 дітей зі ста мільйонів зможуть скласти слово «КОТИГОРОШОК».
Тепер завдання для батьків, просьба вислати коментар, якщо Ваша дитина несвідоо сладе хоч якесь слово хоча би з 4 букв.
Добре розберіться з наведеними прикладами на застосування правил додавання та множення, на їх основі побудований весь наступний матеріал. Попереду ще багато нового матеріалу, тут лише самі основи теорії ймовірностей.


