З цієї статті Ви навчитеся знаходити площу фігури в просторі, яка задана параметричними кривими. Для цього Вам потрібно знати мінімум формул і добрі знання з інтегрування.
Якщо маємо x=x(t), y=y(t) – параметричне рівняння кусково-гладкої простої замкнутої кривої на проміжку [0;T], що проходить проти годинникової стрілки і обмежує зліва від себе фігуру то її площу S знаходимо за формулою
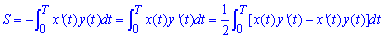 Даний цикл задач в першу чергу полегшить навчання студентам мех-мату Львівського національного університету імені Івана Франка при проходженні практикуму з математичного аналізу. Студенти всіх ВУЗів можуть набиратися практики на таких інтегралах, та вивчати методику обчислення площі.
Даний цикл задач в першу чергу полегшить навчання студентам мех-мату Львівського національного університету імені Івана Франка при проходженні практикуму з математичного аналізу. Студенти всіх ВУЗів можуть набиратися практики на таких інтегралах, та вивчати методику обчислення площі.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:
Площа фігури а) Площа фігури, що обмежена кривими в прямокутних координатах; |
Довжина дуги а) Довжина дуги кривої в прямокутних координатах; |
Об'єм тіла а) Об'єм тіла за відомими поперечними перерізами; |
Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича).
Для запам'ятовування основних моментів схема інтегрування та знаходження площ з прикладу в приклад буде повторюватися. По можливості самі розв'язки будуть проілюстровані підінтегральними кривими.
Прилад 2.100 (2413)Знайти площу фігури, яка обмежена кривими, заданими в параметричній формі x=a(t-sin(t)) , y=a(1-cos(t)) на проміжку [0;2*Pi] і y=0.
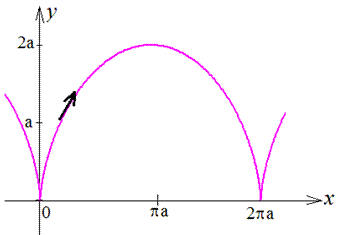
Обчислення: Циклоїда – плоска трансцендентна крива, що визначається кінематично як траєкторія фіксованої точки кола радіуса a, що котиться без ковзання по прямій. Знайдемо похідні по змінній t заданих функцій:
x'=a(1-cos(t));
y'=a*sin(t).
Межі інтегрування відомі за умовою – [0;2*Pi].
Запишемо підінтегральну функцію за формулою x'*y-x*y' (оскільки крива (циклоїда) проходить за ходом годинникової стрілки): 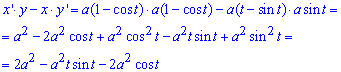
Обчислимо площу фігури обмеженої одною аркою циклоїди:
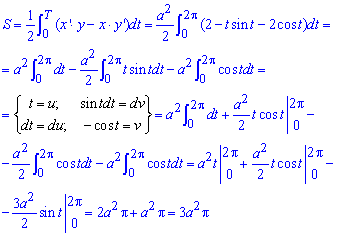
Визначені інтеграли методом інтегрування частинами обчислюються доволі швидко. Також не забувайте, що площа вимірюється в одиницях квадратних.
Приклад 2.101 (2414)Обчислити площу фігури, яка обмежена параметричними кривими x=2t-t2, y=2t2-t3.
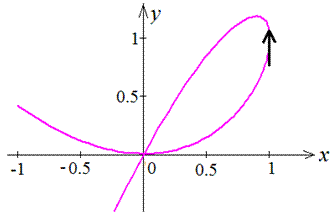
Обчислення: Обчислимо похідні по змінній t від функцій:
x'=2-2t;
y'=4t-3t2.
Знайдемо межі інтегрування – точки перетину кривої, що обмежує задану фігуру: x=0 при t1=0, t2=2 і y=0 при t1=0, t2=2 . Тому маємо період рівний T=2 .
Запишемо підінтегральну функцію за формулою x'*y-x*y' (оскільки крива проходить проти годинникової стрілки):
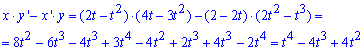 .
.
Обчислимо площу фігури, що обмежена заданою кривою:
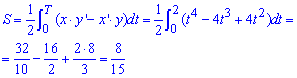
Тут, як бачите, інтеграл знайти взагалі просто, подібних на практичних з математичного аналізу Ви знаходили безліч разів.
Приклад 2.102 (2417.1) Знайти площу фігури, яка обмежена параметричними кривими 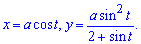
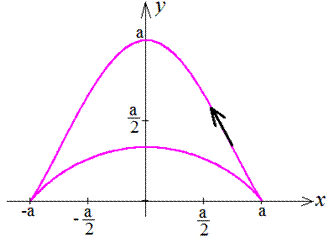
Обчислення: Продиференціюємо функції по змінній t:
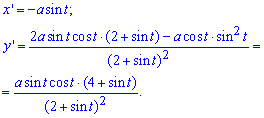 .
.
Запишемо межі інтегрування (потрібно попередньо дослідити функцію): T=[0;2*Pi].
Запишемо підінтегральну функцію за формулою x'*y
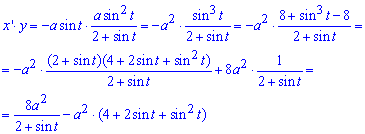
Обчислимо площу фігури за формулою для параметричних кривих:
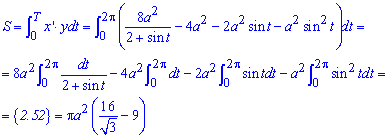
Визначений інтеграл досить простий в плані обчислень.
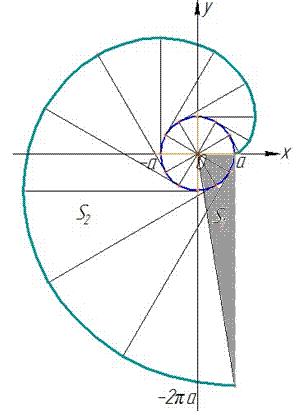
Приклад 2.103 (2415) Знайти площу фігури, обмеженої кривими x=a(cos(t)+t*sin(t)) , y=a(sin(t)-t*cos(t)) (розгортка кола), і x=a , 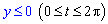 .
.
Обчислення: Знайдемо похідні функцій по змінній t :
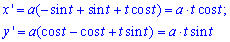
Межі інтегрування виписуємо з початкової умови - [0; 2*Pi].
Виведемо підінтегральну функцію за формулою x'*y-x*y'
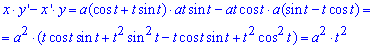 .
.
Обчислимо площу фігури, що обмежена заданою кривою і прямими:
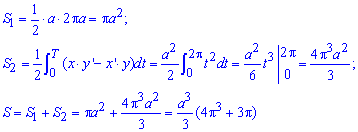
Слід зауважити, що при інтегруванні по куту не враховується площа трикутника S1, що заштрихована сірим.
Без побудови графіка функції врахувати необхідність знаходити додаткову площу доволі важко.
Приклад 2.104 (2416) Знайти площу фігури, обмеженої кривими x=a(2*cos(t)-cos(2t)) , y=a(2*sin(t)-sin(2t)).
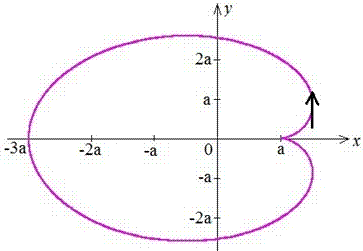
Обчислення: Обчислимо похідні по змінній t заданих функцій:
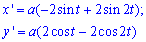
Запишемо межі інтегрування (потрібно попередньо дослідити функцію): 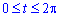 .
.
Складемо рівняння підінтегральної функції за формулою x'*y-x*y'
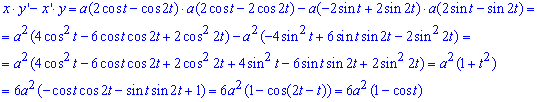 .
.
Далі через визначений інтеграл обчислюємо площу фігури, що обмежена заданою кривою:
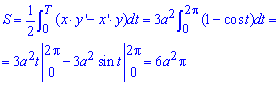
Інтеграл не складний, а кінцева формула проста для розрахунків площі.
Приклад 2.105 (2417) Знайти площу фігури, обмеженої параметричними кривими 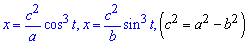 (еволюта еліпса)
(еволюта еліпса)
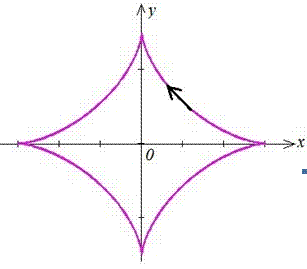
Обчислення: Еволюта – множина точок центрів кривизни кривої. По відношенню до своєї еволюти будь-яка крива є евольвентою (інволютою, тобто розгорткою цієї кривої). Знайдемо похідні функцій по змінній t :
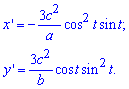
Межі інтегрування рівні: 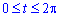
Запишемо підінтегральну функцію за формулою x'*y-x*y':
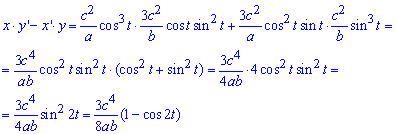
Інтегруванням за періодом знаходимо площу фігури, що обмежена заданою кривою:
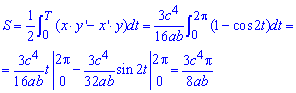
Приклад 2429 Звівши рівняння до параметричного вигляду, знайти площі фігур, обмежених кривими 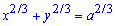 (астроїда).
(астроїда).
Обчислення: Перепишемо рівняння астроїди у вигляді 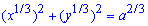 .
.
Нехай x=a*cos3(t), y=a*sin3(t).
Неважко підставити і переконатися, що це саме та підстановка і буде рівнянням астроїди в параметричній формі.
Далі по аналогії з прикладом 2.105 матимемо
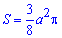
В наступних публікаціях Ви знайдете більше прикладів на знаходження площі фігури за допомогою визначеного інтегралу.


