Якщо крива задана рівнянням 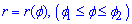 в полярній системі координат, де функція є гладкою неперервною на проміжку
в полярній системі координат, де функція є гладкою неперервною на проміжку 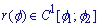 , тоді довжина дуги кривої дорівнює визначеному інтегралу, розрахованому за формулою
, тоді довжина дуги кривої дорівнює визначеному інтегралу, розрахованому за формулою
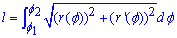
В формулі довжини дуги в полярних координатах під інтегралом маємо кореневу функцію від суми квадратів радіуса та його похідної. Обчислення в певній мірі перегукуються з попередніми публікаціями, з яких Ви вже знаєте як обчислити довжину дуг, які задано в декартовій системі координат та параметрично.
Приклади підібрано із програми практикуму для студентів мех-мату Львівського національного університету імені Івана Франка.
Інші ВУЗи України мають здебільшого легшу програму навчання, завдання схожі, а в ряді випадків співпадають.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:
Площа фігури а) Площа фігури, що обмежена кривими в прямокутних координатах; |
Довжина дуги а) Довжина дуги кривої в прямокутних координатах; |
Об'єм тіла а) Об'єм тіла за відомими поперечними перерізами; |
Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький і ін. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича ).
Для вивчення основних моментів схема інтегрування та формули обчислення дуги кривої, заданої в параметричній формі будуть повторюватися з прикладу в приклад. Частину завдань обов'язково проілюструємо графіками кривих.
Як знайти довжину дуги кривої, заданої в полярних координатах?
Приклад 2.132 (2446)Знайти довжину дуги кривої 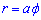 (спіраль Архімеда),
(спіраль Архімеда), 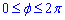 .
.
Обчислення: Знайдемо похідну по змінній 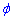 заданої функції:
заданої функції: 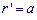
Межі інтегрування відомі за умовою: [0;2Pi].
Запишемо підінтегральну функцію: 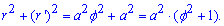 Обчислимо довжину дуги кривої на заданому відрізку:
Обчислимо довжину дуги кривої на заданому відрізку:
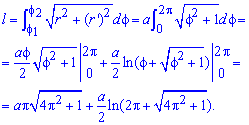 од.
од.
Приклад 2.133 (2447) Знайти довжину дуги кривої 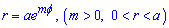 (), .
(), .
Обчислення: Знайдемо похідну по змінній 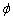 заданої функції:
заданої функції: 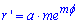
Запишемо межі інтегрування:  при
при 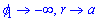 , при
, при 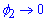 , тому
, тому 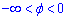 (отримаємо невластивий інтеграл І роду, який є збіжний).
(отримаємо невластивий інтеграл І роду, який є збіжний).
Запишемо підінтегральну функцію:
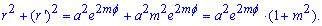
Обчислимо довжину дуги кривої на заданому відрізку:
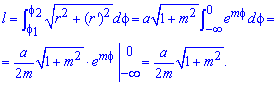 .
.
Приклад 2.134 (2448) Знайти довжину дуги кривої 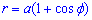 (кардіоїда) (Дивись 2.107).
(кардіоїда) (Дивись 2.107).
Обчислення: Знайдемо похідну по змінній 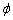 заданої функції:
заданої функції: 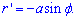
Межі інтегрування: [0;Pi].
(знайдемо довжину половини кривої і помножимо на 2).
Запишемо підінтегральну функцію:
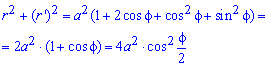
Обчислимо довжину дуги кривої на заданому відрізку:
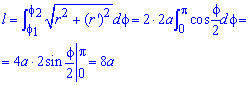 од.
од.
Приклад 2.135 (2450) Знайти довжину дуги кривої 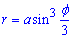 .
.
Обчислення: Знайдемо похідну по змінній 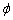 заданої функції:
заданої функції:
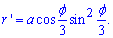
Межі інтегрування: 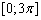 , оскільки задана крива замкнена в цих межах.
, оскільки задана крива замкнена в цих межах.
Запишемо підінтегральну функцію:
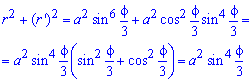
Обчислимо довжину дуги кривої на заданому відрізку:
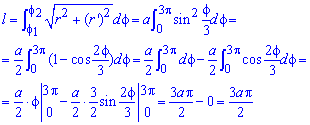 кв. од.
кв. од.
Приклад 2.136 (2449) Знайти довжину дуги кривої 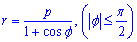 (парабола), (Дивись рис. 2.109)
(парабола), (Дивись рис. 2.109)
Обчислення: Знайдемо похідну по змінній 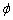 заданої функції:
заданої функції:

Межі інтегрування відомі за умовою: для параболи 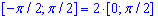 .
.
Запишемо підінтегральну функцію:
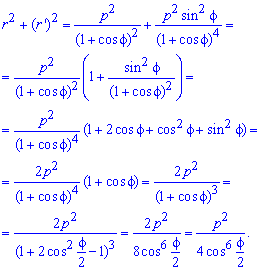
Обчислимо довжину дуги кривої на заданому відрізку:
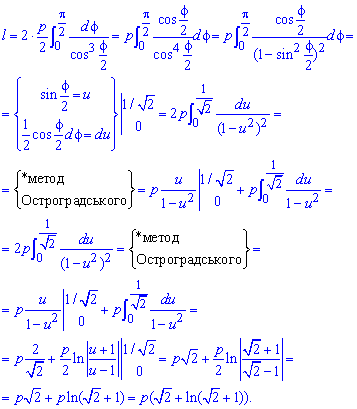
* Метод Остроградського:
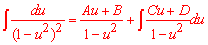 .
.
Візьмемо похідну з кожної частини рівності (з кожного доданку), де 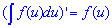
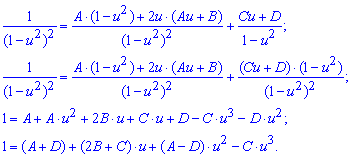
прирівняємо коефіцієнти при кожній змінній з обох частин рівності:
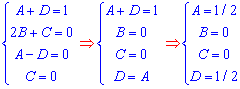
Отримуємо
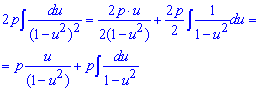 (див. вище).
(див. вище).
Приклад 2.137 (2452.1) Знайти довжину дуги кривої 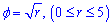 ,
,
Обчислення: Знайдемо похідну по змінній 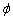 заданої функції:
заданої функції:
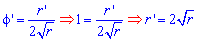
Межі інтегрування відомі за умовою: rє[0;5].
Запишемо підінтегральну функцію: 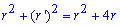
Обчислимо довжину дуги кривої на заданому відрізку:
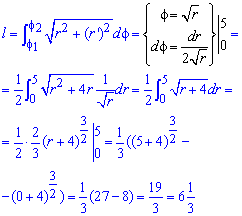 од.
од.
Приклад 2.138 (2452) Знайти довжину дуги кривої 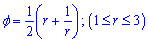 ,
,
Обчислення: Знайдемо похідну по змінній 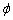 заданої функції:
заданої функції:
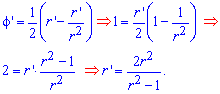
Межі інтегрування відомі за умовою: [1;3].
Запишемо підінтегральну функцію:
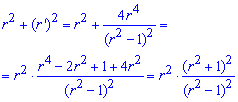 .
.
Обчислимо довжину дуги кривої на заданому відрізку:
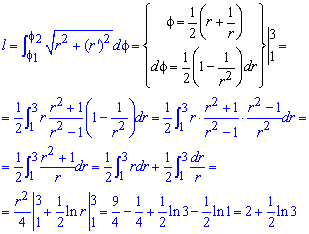 од.
од.
Приклад 2451 Знайти довжину дуги кривої 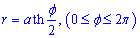 ,
,
Обчислення: Знайдемо похідну по змінній 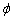 заданої функції:
заданої функції:
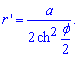
Межі інтегрування відомі за умовою: [0;2Pi].
Запишемо підінтегральну функцію:
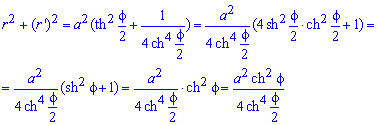 .
.
Обчислимо довжину дуги кривої на заданому відрізку:
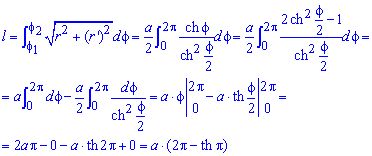 од.
од.
Приклад 2452.2 Знайти довжину дуги кривої 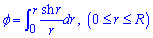 , .
, .
Обчислення: Знайдемо похідну по змінній 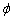 заданої функції:
заданої функції:
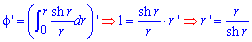
Межі інтегрування відомі за умовою: [0;R]. Запишемо підінтегральну функцію:
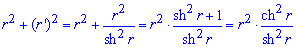
Обчислимо довжину дуги кривої на заданому відрізку:
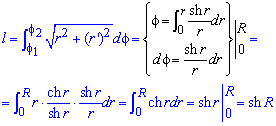 .
.
Приклад 2452.3 Знайти довжину дуги кривої 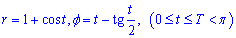 , , .
, , .
Обчислення: Знайдемо похідну 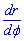 і диференціал
і диференціал 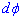 по змінній t заданих функцій:
по змінній t заданих функцій:
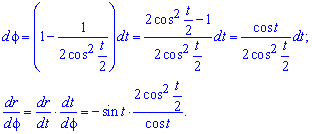
Межі інтегрування відомі за умовою: t[0;T].
Запишемо підінтегральну функцію:
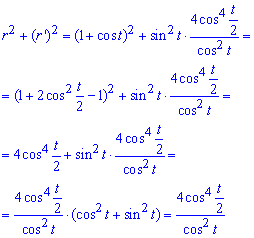
Обчислимо довжину дуги кривої на заданому відрізку:
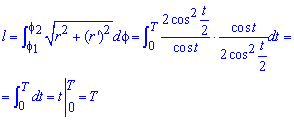
Ось і всі приклади, які ми встигли Вам оформити.


