Площа S криволінійного сектора, обмеженого неперервною кривою r=r(f) і двома променями f=f1 і f=f2, де f1< f2 дорівнює половині визначеного інтегралу від квадрату радіуса кривої, проінтегрованого в межах зміни кута
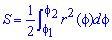 Задачі взяті із програми практикуму для студентів мех-мату Львівського національного університету імені Івана Франка. Студенти всіх ВУЗ-ів України можуть набиратися практики на таких інтегралах, та вивчати методику обчислення площі фігури у полярній системі координат.
Задачі взяті із програми практикуму для студентів мех-мату Львівського національного університету імені Івана Франка. Студенти всіх ВУЗ-ів України можуть набиратися практики на таких інтегралах, та вивчати методику обчислення площі фігури у полярній системі координат.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:
Площа фігури а) Площа фігури, що обмежена кривими в прямокутних координатах; |
Довжина дуги а) Довжина дуги кривої в прямокутних координатах; |
Об'єм тіла а) Об'єм тіла за відомими поперечними перерізами; |
Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича).
Для запам'ятовування основних моментів схема інтегрування та знаходження площ з прикладу в приклад буде повторюватися. По можливості самі розв'язки будуть проілюстровані графіками досліджуваних кривих.
Знайти площі фігур, обмежених кривими, заданими в полярних координатах
Приклад 2.106 (2418) Обчислити площу фігури, обмеженої кривими r2=a2*cos(2f) (лемніската Бернуллі).
Обчислення: Лемніската Бернуллі – геометричне місце точок, добуток відстаней від яких до двох фіксованих точок (фокусів) залишається постійним і дорівнює квадрату половини відстані між фокусами.
Запишемо підінтегральну функцію: r2=a2*cos(2f) (відома за умовою).
Знайдемо межі інтегрування: Задана крива замкнена, симетрична відносно прямих r*cos(f)=0 і r*sin(f)=0.
Наведемо графік лемніскати Бернуллі
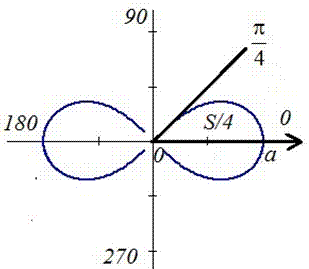
Оскільки задана функція осями координат ділиться на чотири рівні частини і досягає своїх критичних значень при f1=0 (r=a) і f2=p/4 (r=0) , то площу фігури обчислимо для однієї частини лемніскати, а результат помножимо на 4.
Знайдемо площу фігури інтегруванням по куту
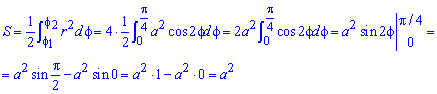
Площа вимірюється в одиницях квадратних, проте в цьому та наступних прикладах розмірності наводити не будемо, хоча про них пам'ятаємо.
Приклад 2.107 (2419) Знайти площу фігури, обмеженої кривими r=a*(1+cos(f)) – кардіоїда.
Обчислення: Кардіоїда – плоска лінія, яка описується фіксованою точкою кола, що котиться по нерухомому колі з таким же радіусом a.
Записуємо підінтегральну функцію: r2=a2*(1+cos(f))2.
Знаходимо межі інтегрування: Задана крива замкнена, симетрична відносно прямої r*sin(f)=0.
Оскільки задана функція осями координат ділиться на дві рівні частини і досягає своїх критичних значень при f1=0 (r=2a) і f2=p (r=0) , то площу фігури обчислимо для половини кардіоїди, а результат помножимо на 2. Графік кардіоїди має вигляд
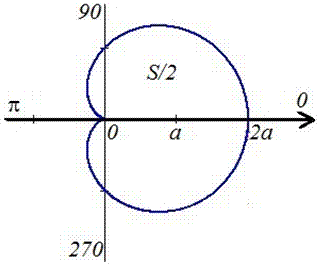
Обчислимо площу фігури, що обмежена заданою кривою:
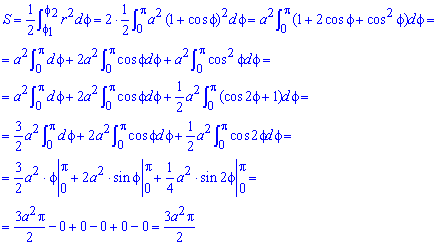
Приклад 2.108 (2420) Знайти площу фігури, обмеженої кривою r=a*sin(f) -трилисник.
Обчислення: Підносимо до квадрату, щоб отримати підінтегральну функцію: r2=a2*sin2(f).
Графік трилисника в полярній системі координат
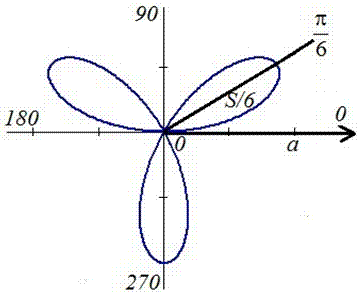
Встановимо межі інтегрування: Оскільки заданий графік функції ділиться на шість рівних частин (півпелюсток) і досягає своїх критичних значень при f1=0 (r=0) і f2=p/6 (r=a/2), то площу фігури обчислимо для однієї частини фігури, а результат помножимо на 6.
Знаходимо площу фігури інтегруванням по куту
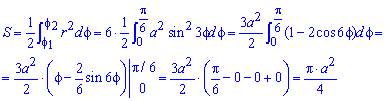
Отримали просту для обчислень формулу площі трилисника S=Pi*a2/4.
Приклад 2.109 ( 2421) Обчислити площу фігури, обмеженої кривою 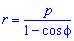 (парабола), f1=p/4, f2=p/2.
(парабола), f1=p/4, f2=p/2.
Обчислення: Підносимо до квадрату рівняння кривої в полярній системі координат (СК).
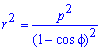
Межі інтегрування відомі f1=p/4, f2=p/2 за умовою.
Графік фігури, площу якої потрібно знайти має вигляд
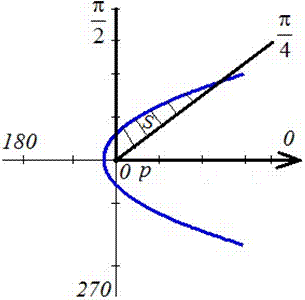
Інтегруванням обчислюємо площу фігури, що обмежена параболою:
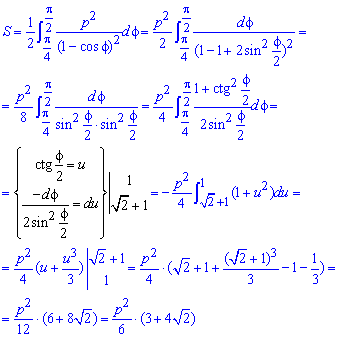
Для обчислення інтегралу слід виконати заміну змінних, при цьому не забувайте, що зміняться межі інтегрування.
Приклад 2.110 ( 2422) Знайти площу фігури, обмеженої кривою 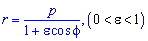 (еліпс)
(еліпс)
Обчислення: Запишемо підінтегральну функцію:
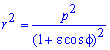
Запишемо межі інтегрування: f1=0, f2=2p (початок і кінець кривої еліпса).
Графік еліпса має вигляд
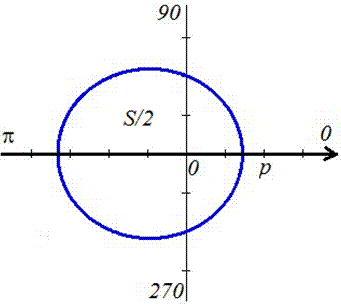
Знаходимо площу еліпса, скориставшись наступною формулою інтегрування
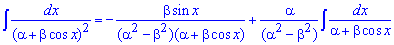
При виведенні цієї формули користувались методом інтегрування частинами!
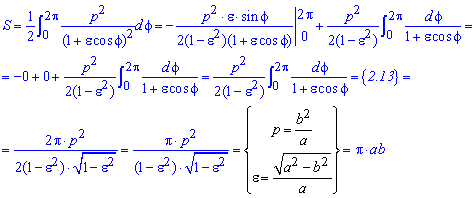
Вкінці перетворюємо кінцеву формула за допомогою відомих позначень.
Як бачимо, відповіді задач 2.110 і 2.87 співпадають, тобто площа еліпса S=Pi*a*b.
Приклад 2.111 (2422.1) Знайти площу фігури, обмеженою кривою заданою в полярних координатах r=3+2*cos(f).
Обчислення: Спершу знаходимо підінтегральну функцію: r2=(3+2*cos(f))2.
Далі межі інтегрування: задана крива замкнена, симетрична відносно прямої r*sin(f)=0. Її графік наведено на рисунку нижче
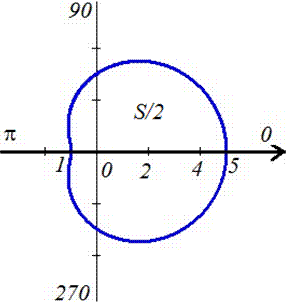
Оскільки задана крива осями координат ділиться на дві рівні частини і досягає своїх критичних значень при кутах f1=0 (r=5) і f2=p (r=1) , то обчислимо половину площі фігури, а результат помножимо на 2.
Знаходимо площу фігури через визначений інтеграл
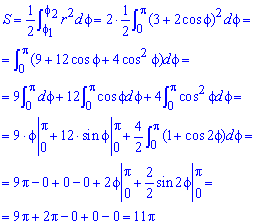
Інтеграл в даному випадку не важкий і, піднявши до квадрату підінтегральну функцію та, понизивши квадрат косинуса, в результаті обчислень отримаємо, що площа рівна S=11*Pi.
Приклад 2.112 (2424.1)Знайти площу фігури, обмеженою кривою заданою в полярних координатах r2+f2=1.
Обчислення: Виразимо підінтегральну функцію: r2=1-f2 .
Знайдемо межі інтегрування. 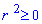 , тому
, тому 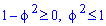 , звідки
, звідки 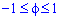 .
.
Побудуємо графік кривої в математичному пакеті Maple17.
Крива складається із двох віток кореневої функції, тому для коректного її відображення використовуємо наступний код:
> restart;
> with(plots):
> q1:=plot(sqrt(1-phi^2),phi=-1..1,color=blue,thickness=2,coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1..1,color=blue,thickness=2,coords=polar):
> display(q1,q2);
Фрагмент програми Maple наведено нижче
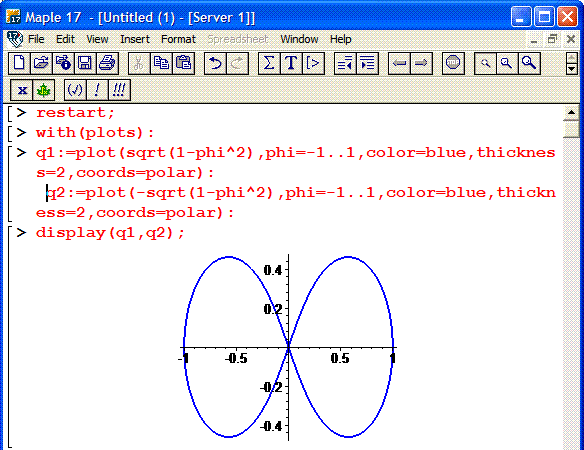
Знаходимо площу фігури, що обмежена наведеною кривою:
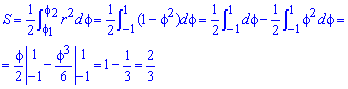
Інтеграл в цьому завданні найлегший з усіх, що розглядалися.
Приклад 2.113 ( 2422.2) Обчислити площу фігури, обмеженої кривими 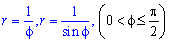 .
.
Обчислення: Виписуємо підінтегральні функції:
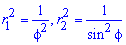
Оскільки на проміжку інтегрування 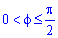 між кривими справджується нерівність
між кривими справджується нерівність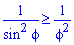 , то для знаходження площі маємо r22-r12.
, то для знаходження площі маємо r22-r12.
Знайдемо межі інтегрування: f1=0 - особлива точка (функція прямує до безмежності), f1=p/2 (відомі за умовою).
Знаходимо площу фігури через границю від інтегралу:
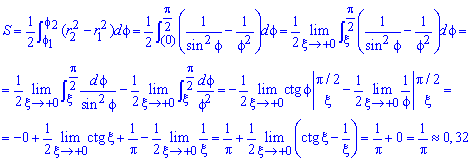
Даний приклад добре розберіть, щоб не мати труднощів на екзамені чи модулі.
Приклад 2.114 ( 2424) Обчислити площу фігури, обмеженої кривою 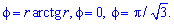
Обчислення: Запишемо підінтегральну функцію: r2.
Запишемо межі інтегрування: 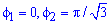 (відомі за умовою).
(відомі за умовою).
Графік функцій має вигляд
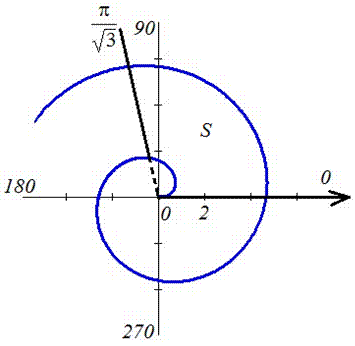
Обчислимо площу фігури, що наведено на графіку. Для цього спершу знаходимо диференціал кута f та переходимо до інтегрування по радіусу.
Для знаходження інтегралу застосовуємо інтегрування частинами
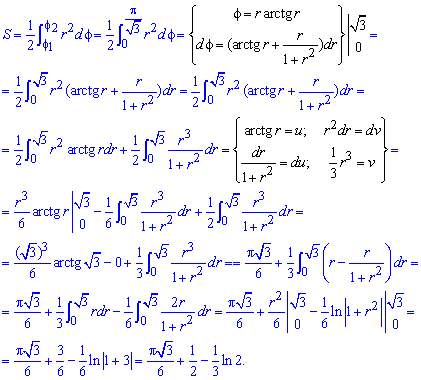
Інтеграл доволі важко знаходиться, тож все що містить формула уважно проаналізуйте.
Приклад 2.115 (2424.3) Знайти площу фігури, обмеженої кривими f=4r-r3,f=0.
Обчислення: Запишемо підінтегральну функцію: r2.
Її графік в полярній системі координат має вигляд
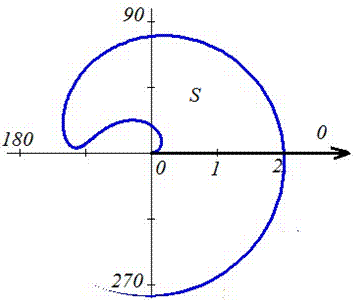
Встановимо межі інтегрування: При зростанні r від 0 до 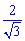 кут зростає, при зростанні r від
кут зростає, при зростанні r від 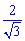 до 2 кут спадає, тому величина інтеграла в межах
до 2 кут спадає, тому величина інтеграла в межах 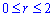 має знак «мінус».
має знак «мінус».
Обчислимо площу фігури інтегруванням: при цьому знайдемо диференціал по куту та перейдемо до інтегрування за радіусом:
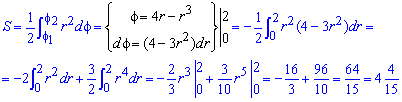
Перед інтегралом (після заміни змінних) поставили знак «мінус», оскільки інтеграл є від'ємним на цьому проміжку, а площа повинна бути більше нуля.
Приклад 2.116 (2424.4) Знайти площу фігури, обмеженої полярними кривими f=r-sin(r), f=p.
Обчислення: Підінтегральну функція наступна: r2.
Межі інтегрування: f1=0, (r=0) початок; f1=p (відомо за умовою).
Графік функції має вигляд
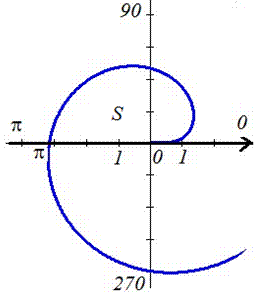
Знаходимо площу фігури застосовуючи двічі інтегрування частинами
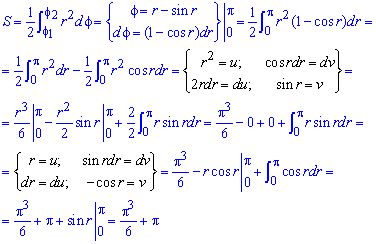
Інтеграл не надто складний, всі переходи просьба проаналізувати самостійно.
Приклад 2423 Обчислити площу фігури, обмеженої полярними кривими r=a*cos(f), r=a(cos(f)+sin(f)), M(a/2;0)єS.
Обчислення: Для уявлення фігури, площу якої потрібно знайти попередньо виконуємо побудову графіка заданих функцій
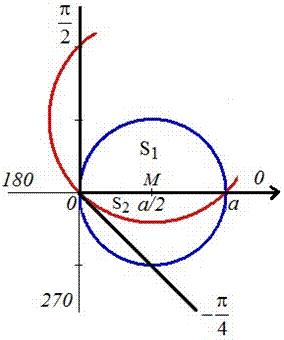
Оскільки точка M(a/2;0)єS ділить шукану площу на дві частини, то маємо два інтеграли
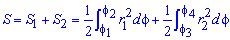
Записуємо рівняння підінтегральних функцій:
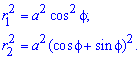
Визначаємо межі інтегрування: 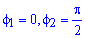 , де
, де 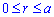 і
і 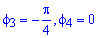 де
де 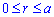 (точки перетину ліній).
(точки перетину ліній).
Обчислюємо площу зображеної фігури інтегруванням
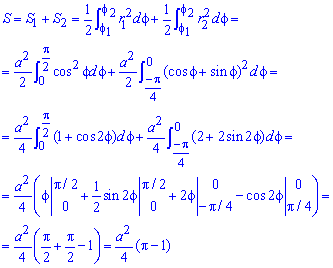
Тут скористалися відомими тригонометричними формулами для пониження степеня косинусів та синусів під інтегралом. Все решта зводиться до застосування простих формул інтегрування, та знаходження їх значень.
Приклад 2424.2 Знайти площу фігури, обмеженої полярними кривими f=sin(p*r), r є[0;1].
Обчислення: Запишемо підінтегральну функцію: r2.
Запишемо межі інтегрування: При зростанні r від 0 до 1/2 кут f зростає з 0 до 1 , при зростанні r від 1/2 до 1 кут f спадає з 1 до 0, тому величина інтеграла в межах r є[0;1]має знак «мінус».
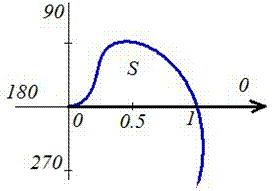
Знаходимо площу фігури, попередньо перейшовши до нової змінної під інтегралом:
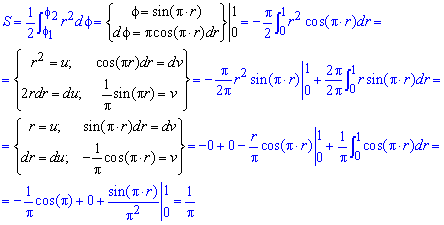
Перед інтегралом (після заміни змінних) поставили знак «мінус», оскільки інтеграл є від'ємним на цьому проміжку, а площа повинна бути більшою нуля.
Приклад 2425 Знайти площу фігури, обмеженої кривою в полярній системі координат, заданою параметрично 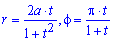
Обчислення: Складаємо вираз для підінтегральної функції та диференціал кута:
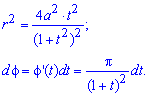
Встановлюємо межі інтегрування за параметром: Оскільки 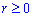
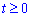 : r=0 при t=0 і
: r=0 при t=0 і  при
при 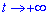 , тому маємо межі інтегрування від нуля до безмежності
, тому маємо межі інтегрування від нуля до безмежності 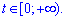
Графік кривої має вигляд.
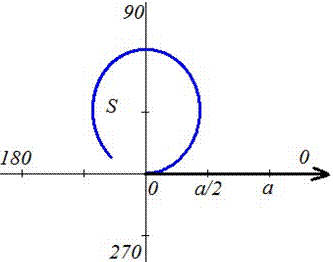
Обчислимо площу наведеної фігури:
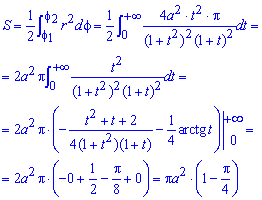
При інтегруванні параметричної функції скористалися методом Остроградського:
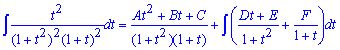
Візьмемо похідну в кожній частині рівності і прирівняємо відповідні коефіцієнти:
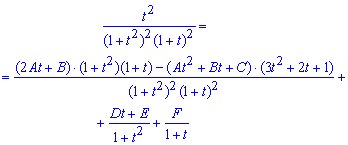
Звідси, A=-1/4; B=-1/4; C=-1/2; D=0;E=-1/4; F=0.
Перейти до полярних координат і знайти площі фігур, обмежених кривими
Приклад 2426 Перейти до полярних координат і знайти площу фігури x3+y3=3a*x*y (лист Декарта)
Обчислення: Перейдемо від прямокутної системи координат до полярної системи координат за формулами переходу:
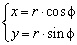
При підстановці в рівняння отримаємо
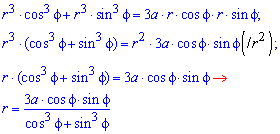
Піднесемо до квадрату, щоб отримати підінтегральну функцію:
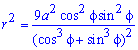
Випишемо межі інтегрування: 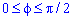 , бо
, бо 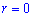 при
при 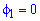 і при
і при 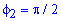 .
.
Графік функції має вигляд
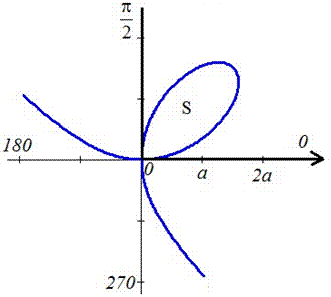
Знайдемо площу фігури інтегруванням:
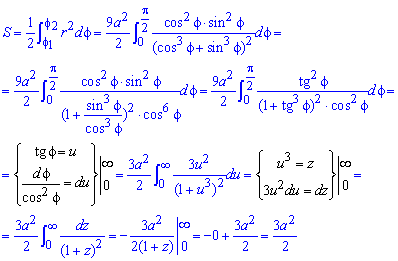
Для отримання кінцевої формули площі дві застосовували заміну змінних під інтегралом.
Уважно розберіть, як при цьому змінюються межі та ефективність методики.
Приклад 2427 Перейти до полярних координат і знайти площу фігури x4+y4=3a2(x2+y2)
Обчислення: Переходимо від прямокутної до полярної системи координат:
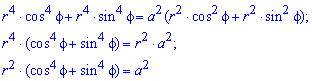
Виразимо підінтегральну функцію діленням:
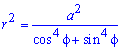
Запишемо межі інтегрування: 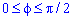 (функція парна).
(функція парна).
Її графік зображено на рисунку
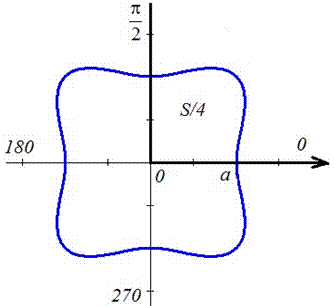
Осі прямокутної системи координат є осями симетрії для фігури, що обмежена заданою лінією, тому площу знайдемо для симеричної частини і результат помножимо на 4.
Знаходимо площу фігури, що обмежена зображеною кривою:
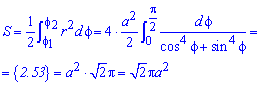
Приклад 2428 Перейти до полярних координат і знайти площу фігури (x2+y2)2=2a2*x*y (лемніската).
Обчислення: Виконуємо перехід від прямокутної до полярної системи координат:
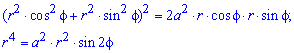
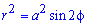 - підінтегральна функція.
- підінтегральна функція.
Графік досліджуваної кривої наступний
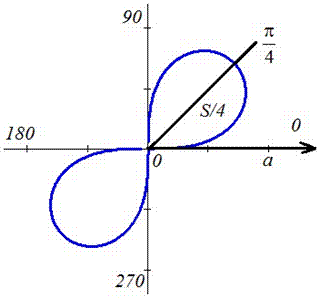
Запишемо межі інтегрування: враховуючи симетрію точок лемніскати відносно прямої r*sin(f)=r*cos(f) і відносно початку координат, то площу фігури шукатимемо в межах 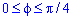 і результат помножимо на 4 (дивись приклад 2.106).
і результат помножимо на 4 (дивись приклад 2.106).
Знаходимо площу фігури інтегруванням:
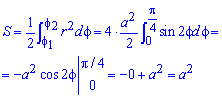
Обчислень в цьому завданні мінімум.
В наступних публікаціях Ви знайдете більше прикладів на застосування визначеного інтегралу при обчисленні довжини дуги, об'ємів фігур обертання та площ поверхонь.


