Як знайти довжину дуги в прямокутних координатах?

Довжина дуги відрізку l гладкої кривої y=y(x) на проміжку xє[a;b] дорівнює визначеному інтегралу
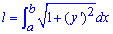- формула для обчислення довжини дуги кривої в прямокутних координатах.
З формули бачимо, що для обчислення довжини дуги кривої необхідно обчислити квадрат похідної від функції та підставити в інтеграл від кореневої функції.
Все решта залежить від Ваших умінь інтегрувати.
Далі будуть наведені готові задачі взяті із програми практикуму для студентів мех-мату Львівського національного університету імені Івана Франка.
Студенти інших ВУЗів України можливо мають схожу програму навчання, завдання схожі або співпадають.
Загалом вивчайте методику знаходження довжини дуги кривої та методи інтегрування.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:

Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича).
Для запам'ятовування основних моментів схема інтегрування та обчислення дуги кривої з прикладу в приклад буде повторюватися. По можливості самі розв'язки будуть проілюстровані графіками кривих.

Знайти довжини дуг кривих в прямокутній системі координат

Приклад 2.117 (2431) Обчислити довжину дуги кривої y=x^3/2 (півкубічна парабола Нейля), xє[0;4] .
Обчислення: Знайдемо похідну заданої функції по змінній x :

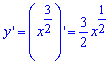
Графік півкубічної параболи Нейля має вигляд

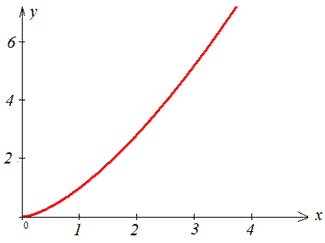
Виписуємо межі інтегрування: a=0, b=4 (відомі за умовою).
За формулою знаходимо довжину дуги на заданому відрізку:

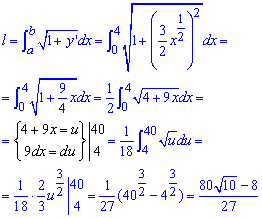
Під час інтегрування для приведення підінтегральної функції до табличного вигляду виконали заміну змінних. При цьому потрібно перераховувати межі інтегрування.
В результаті довелося інтегрувати кореневу функцію, а довжина дуги після обчислень приблизно рівна l=9,07.
Пам'ятайте, що усі довжини вимірюються в одиницях (од.)!!!
.

Приклад 2.118 (2432) Знайти довжину дуги кривої y²=2px (парабола), xє[0;x₀].
Обчислення: Оскільки відрізок дуги параболи заданий в межах [0;x₀], то задана функція матиме вигляд додатної вітки кореневої функції .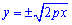
Обчислимо похідну функції по змінній x :

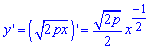
Запишемо межі інтегрування: a=0, b=x₀ з умови.
Графік параболи наведено нижче

Обчислимо довжину дуги через визначений інтеграл. Для зведення до простих формул інтегрування застосовуємо заміну змінних, при цьому не забуваємо перерахувати зміну меж інтегрування:

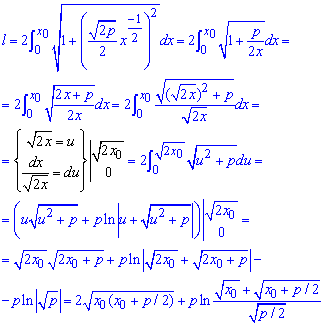
В кінці обчислень застосовано інтегрування частинами.

Приклад 2.119 (2434) Знайти довжину дуги кривої y=e^x , [0;x₀].
Обчислення: Для інтегрування знаходимо похідну (по змінній x) експоненти :
y'=(e^x)'=e^x.
Оскільки показник не містить ніяких коефіцієнтів при змінній, то похідна рівна самій експоненті.
З початкової умови виписуємо межі інтегрування: a=0, b=x₀.
Графік експоненти має вигляд

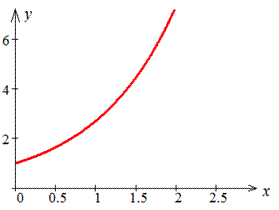
Щоб обчислити довжину дуги експоненти переходимо до нової змінної. Це веде до зміни і меж інтегрування і самого диференціалу:

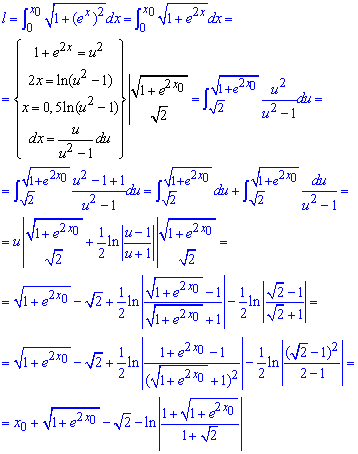
Вкінці розрахунків приходимо до формули дуги, що містить кореневу та логарифмічну залежності від біжучої координати.

Приклад 2.120 ( 2435) Знайти довжину дуги кривої x=1/4y²-ln(y)/2 , yє[1;e].
Обчислення: Обчислимо похідну (по змінній y ) заданої функції :

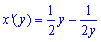
Наведена формула працює і для обернених функцій x=x(y), особливо якщо функція змінюється як показано на графіку

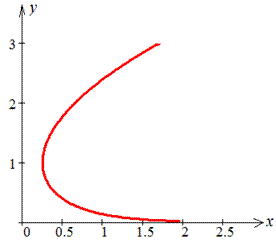
Межі інтегрування: a=1, b=e .
Знаходимо довжину дуги кривої на заданому відрізку:

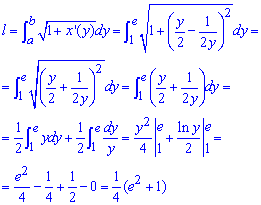
При піднесенні до квадрату похідної отримаємо просту для інтегрування функцію, яка в результаті дає l=(e²+1)/4.

Приклад 2.121 (2436) Обчислити довжину дуги кривої
Обчислення: Знайдемо похідну по змінній x функції:

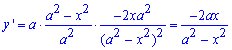
Межі інтегрування для цієї дуги рівні [0;b].
Графік досліджуваного логарифма має вигляд:

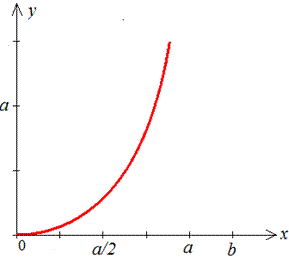
Інтегруванням знаходимо довжину дуги кривої:

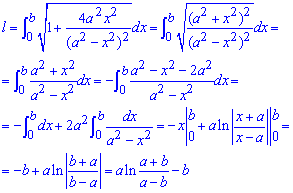
З усіма перетвореннями підінтегральної функції спробуйте розібратися самостійно.

Приклад 2.122 (2437) Обчислити довжину дуги кривої y=ln(cos(x)), 0<x<a<Pi/2.
Обчислення: Знайдемо похідну (по змінній x) заданої функції :

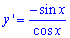
Запишемо межі інтегрування: 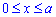(відомі за умовою).

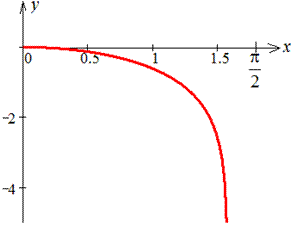
Обчислимо довжину дуги кривої на заданому відрізку:

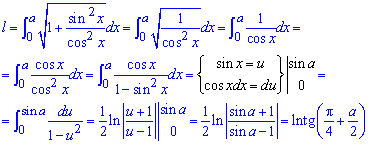
Якщо скористатися тригонометричними формулами то перейдемо до тангенса, а сама довжина дуги рівна l=ln(tg(Pi/4+a/2)).

Приклад 2.123 Знайти довжину дуги кривої y=ln(x) ,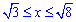
Обчислення: Обчислюємо похідну від логарифма:
y'=1/x.
Межі інтегрування переписуємо з умови: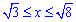
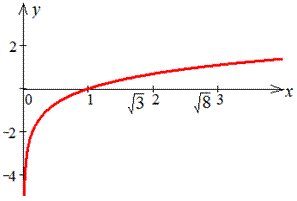
Графік логарифма має вигляд

Інтегрування по довжині дуги доволі непросте, вимагає добрих умінь інтегрувати. 
Розписавши підінтегральну функцію, та застосувавши заміну змінних до одного з інтегралів, приходимо до логарифмів, які при вказаних межах інтегрування дещо спрощуються.

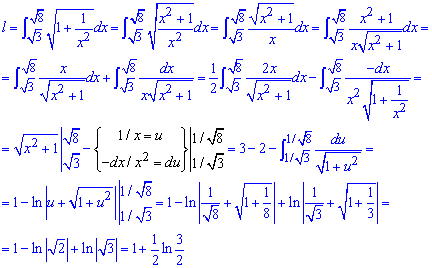
Незважаючи на триповерхові вирази кінцеве значення довжини дуги виражено простою залежністю.

Приклад 2.124 Знайти довжину дуги кривої y=ln(1-x₂), x[0;0,5].
Обчислення: Знайдемо похідну (по змінній x ) заданої функції :

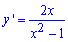
З початкової умови маємо такі межі інтегрування: [0;0,5].
Графік досліджуваного логарифма має вигляд

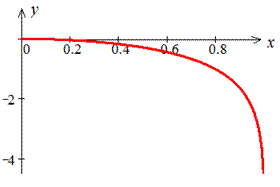
Обчислюємо довжину дуги логарифма:

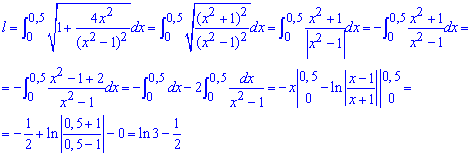
Якщо округлити кінцеве значення, то матимемо l=0,5986.

Приклад 2.125 (2439) Обчислити довжину дуги кривої ,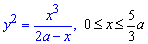
Обчислення: Оскільки графік заданої функції симетричний відносно осі Ox, то обчислимо довжину дуги для половини функції

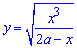
і результат помножимо на 2.
Знайдемо похідну функції та саму підінтегральну функцію:

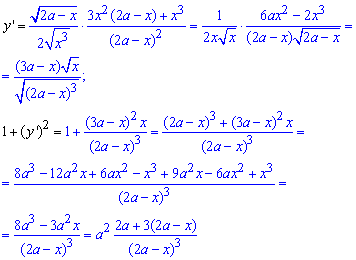
Межі інтегрування відомі з умови: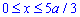
Графік віток в декартовій площині має вигляд.

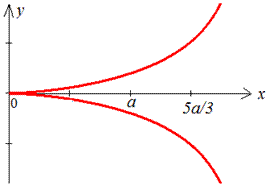
При знаходженні довжину дуги двічі виконуємо заміну змінних.
Як і у попередніх прикладах відповідь отримуємо через логарифми

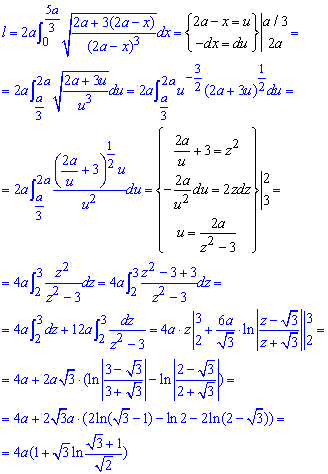
Кому в навчанні доведеться обчислювати подібне завдання, просьба розібратися з перетвореннями. А ще краще - придумати і розв'язати подібний приклад.

Приклад 2.126 (2438) Знайти довжину дуги кривої 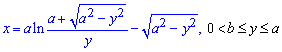(трактриса).
Обчислення: Запишемо похідну за змінною y від трактриси (див. 2408):

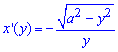
Межі інтегрування за умовою: .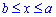
Графік трактриси має вигляд

За формулою дуги кривої виконуємо знаходимо довжину трактриси:

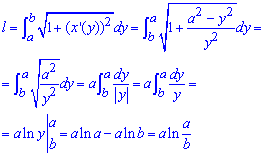
Кінцева формула досить проста для розрахунків. Від краю слід дещо відійти, в іншому випадку довжина трактриси прямує до безмежності.

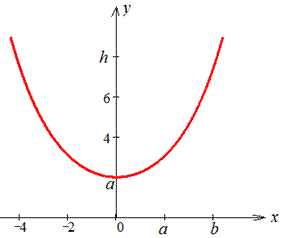
Приклад 2433 Знайти довжину дуги кривої 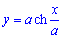(ланцюгова лінія) від точки A(0;a) до точки B(b;h) .
Обчислення: Ланцюгова лінія – це крива, форму якої приймає ланцюг (нитка) під дією сили тяжіння, який підвішений за обидва кінці.
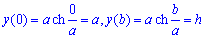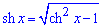Оскільки і , то

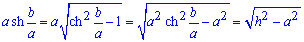
Знайдемо похідну від трактриси :

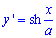
Межі інтегрування по аргументу наступні: .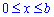

Обчислимо довжину дуги кривої на заданому відрізку:

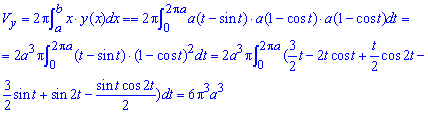
Приклад 2440 Знайти довжину дуги астроїди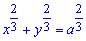
Обчислення: Для астроїди осі прямокутної системи координат ділять лінію на 4 частини (дивись 2429), тому довжину шукатимемо для однієї частини і результат помножимо на 4.
Виразимо функцію для однієї частини астроїди

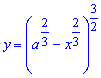
Знайдемо похідну від отриманої залежності та підінтегральну функцію :

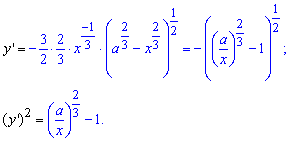
Межі інтегрування: [0;a] (для четвертини астроїди).
Знайти довжину дуги астроїди на практиці достатньо легко:

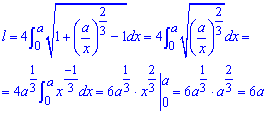
Все в тому, що одиниці скорочуються і отримуємо простий табличний інтеграл.
В результаті довжина астроїди рівна l=6a.