Площа поверхні обертання кривої навколо осі

Площа поверхні P, що утворена обертанням гладкої кривої AB навколо осі Ox де y(x) - неперервна невід'ємна функція дорівнює
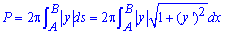, де ds - диференціал дуги.

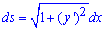
Основні формули теорії розрахунку площі поверхні Ви маєте, тепер перейдемо до прикладів, що Вас чекають на практиці та екзаменах.
Завдання підібрано із навчальної програми для студентів мех-мату Львівського національного університету імені Івана Франка.
Інші ВУЗи мають подібну програму навчання, завдання схожі, а в ряді випадків ті ж самі.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:

Номер в прикладах відповідає номеру зі збірника Б. П. Демидовича. Для вивчення основних моментів формули інтегрування для обчислення площі поверхні обертання будуть повторюватися з прикладу в приклад. Частину завдань проілюструємо графіками кривих.

Приклад 2486 Знайти площу поверхні обертання кривої 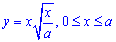навколо осі Ox.
Розв'язання: Знайдемо диференціал дуги: для цього обчислюємо похідну функції та, піднісши до квадрату, підставляємо у формулу

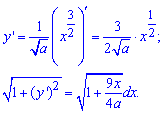
Запишемо межі інтегрування (відомо за умовою): .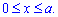
Інтегруванням знаходимо площу поверхні обертання:

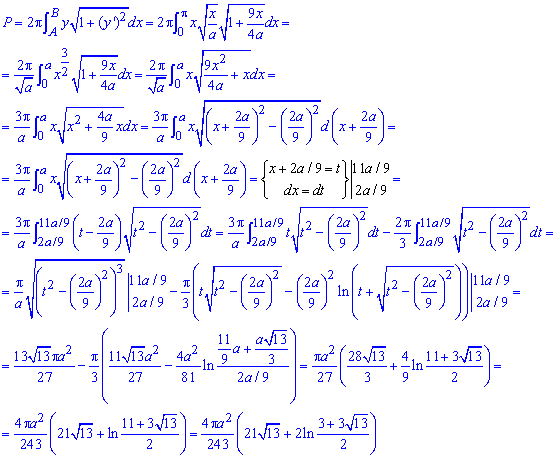
Як бачите найбільше труднощів виникає при знаходженні інтегралу. Тут довелося виділити повні квадрати під коренем, а далі перейти до нової змінної під інтегралом. Не забувайте, що це призводить до зміни меж інтегрування. Також тут і в наступних прикладах шукатимемо лише інтеграл, те що площа вимірюється в одиницях квадратних Ви повинні знати ще із школи.

Приклад 2487 Знайти площу поверхні обертання кривої 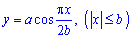навколо осі Ox.
Розв'язання: Обчислюємо диференціал дуги кривої:

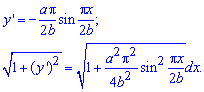
За умовою межі інтегрування : xє[-b;b]..
За формулою знаходимо площу поверхні обертання:

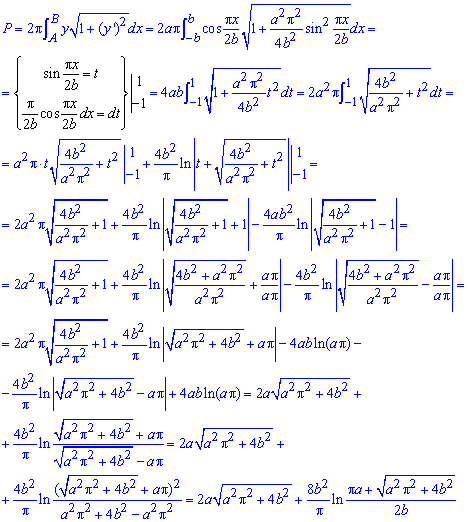
Тут також під інтегралом переходимо до нової змінної, далі після зведення до табличних інтегралів підставляємо межі і спрощуємо логарифми.

Приклад 2492 Знайти площу поверхні обертання астроїди 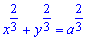навколо осі Ox. (Дивись 2429)
Розв'язання: Записуємо рівняння астроїди в параметричному вигляді:

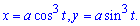
Знаходимо диференціал дуги параметрично заданої кривої за формулою:

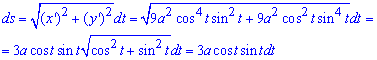
Зауважте, що для параметрично заданої кривої формула дещо інша.
Запишемо межі інтегрування: 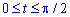і при інтегруванні результат помножимо на 2 (в силу симетрія).
Обчислимо площу поверхні обертання:

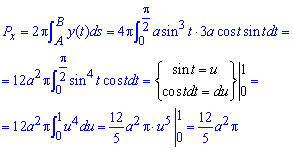
Заміна змінних спрощує інтегрування.

Приклад 2495 Знайти площу поверхні обертання кривої, заданої параметрично x=a(t-sin(t)), y=a(1-cos(t)),t[0;2Pi]
а) навколо осі Ox;
б) навколо осі Oy;
в) навколо прямої y=2a.
Розв'язання: Знайдемо диференціал дуги параметрично заданої кривої:

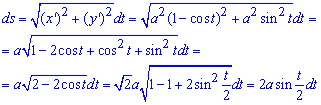
При спрощенні використали відомі тригонометричні залежності.
Межі інтегрування (відомо за умовою): .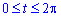
Знайдемо площу поверхні обертання навколо осей:
а)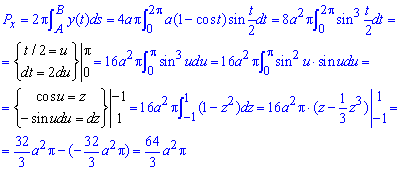
б)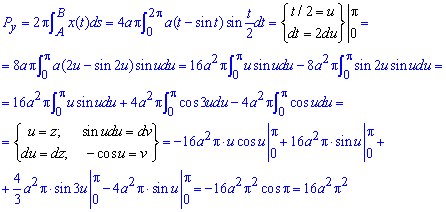
в) площа поверхні обертання навколо прямої y=2a

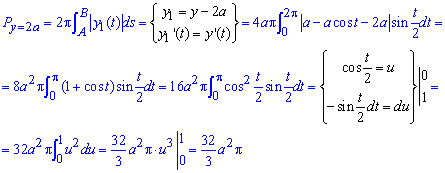
Тут використали симетрію відносно прямої x₁=a*Pi, тому результат помножили на 2.

Приклад 2497 Знайти площу поверхні обертання кардіоїди 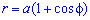навколо полярної осі.

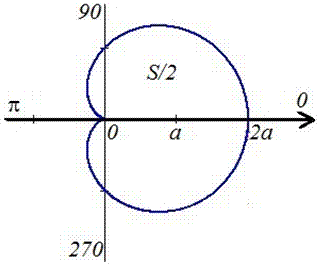
Розв'язання: Для кривої заданої в полярних координатах диференціал дуги знаходимо за формулою:

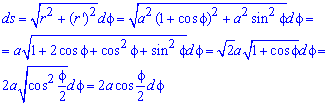
Межі інтегрування: .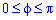
Обчислимо площу поверхні обертання кардіоїди:

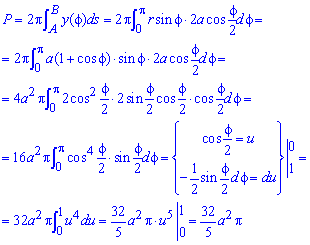
Тут також використовували заміну змінних під інтегралом.

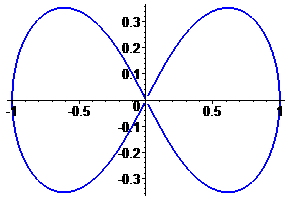
Приклад 2498 Знайти площу поверхні обертання лемніскати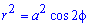
а) навколо полярної осі;
б) навколо осі phi=Pi/2;
в) навколо осі phi=Pi/4.

Розв'язання: Знайдемо диференціал дуги ():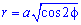

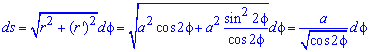
а) Межі інтегрування: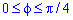
Результат помножимо на 2 в силу симетрії графіку.
Інтегруванням визначаємо площу поверхні обертання лемніскати навколо полярної осі:


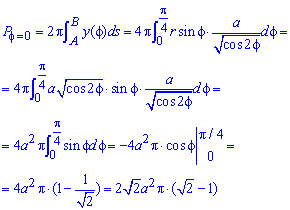
б) Запишемо межі інтегрування: 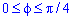і результат помножимо на 2 (симетрія)
Знаходимо площу поверхні обертання лемніскати під кутом phi=Pi/2:

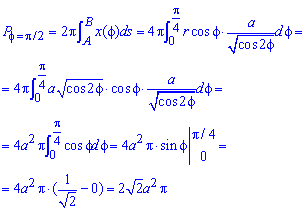
Формули переходу від прямокутної до полярної системи координат : 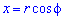і .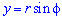

в) Нехай промінь 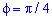буде полярною віссю системи 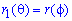, де 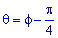. Тоді .
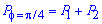Межі інтегрування: В системі координат 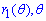, маємо: 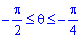для P₁ і 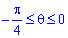для P₂.
З урахуванням симетрії точок кривої, переходячи до системи координат 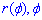, будемо мати 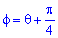: 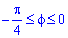для P₁; 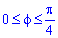для P₂.
Знаходимо площі поверхонь обертання


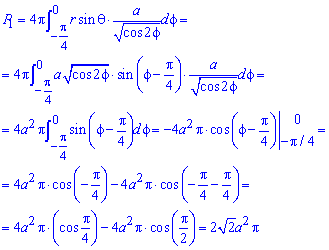
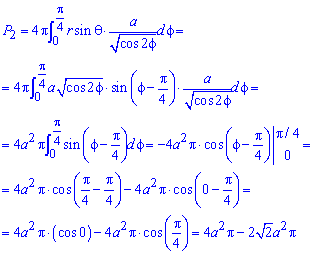
та сумуємо їх

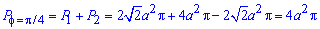
Використана література:
1. Практикум з математичного аналізу. Частина 2. Заболоцький М. В., Фединяк С. І., Філевич П. В. – Львів: Видавничий центр ЛНУ імені Івана Франка, 2006. – 68 с.
2. Демидович Б. П. Сборник задач и упражнений по математическому анализу. Учебное пособие для студентов физических и механико-математических специальностей ВУЗов.–9-е изд.–М.: Наука, главная редакция физико-математической литературы, 1977. – 528 с.
3. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, том ІІ: – М.: Наука, главная редакция физико-математической литературы, 1966. – 800 с.
4. Справочное пособие по математическому анализу, часть І –К.: «Вища школа», 1978. – 696 с.