Из настоящей статьи Вы научитесь находить площадь фигуры в пространстве, которая задана параметрическими кривыми.
Для этого Вам нужно знать минимум формул и хорошые знания из интегрирования.
Если имеем x=x(t), y=y(t) - параметрическое уравнение кусково-гладкой простой замкнутой кривой на промежутке [0;T], что проходит против часовой стрелки и ограничивает слева от себя фигурой то ее площадь S находим за формулой
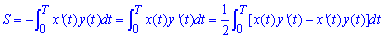Данный цикл задач в первую очередь облегчит учебу студентам мех-мату Львовского национального университета имени Ивана Франко при прохождении практикума из математического анализа.
Студенты всех Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления площади.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. "Практикум из математического анализа" (рядом стоит номер из сборника Б. П. Демидовича).
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы подинтегральными кривыми.
Прибор 2.100 (2413) Найти площадь фигуры, которая ограничена кривыми, заданными в параметрической форме x=a(t-sin(t)), y=a(1-cos(t)) на промежутке [0;2*Pi] и y=0.
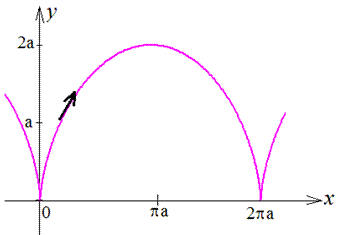
Вычисление: Циклоида - плоская трансцендентная кривая, которая определяется кинематически как траектория фиксированной точки круга радиуса a, что катится без скольжения по прямой.
Найдем производные по переменной t заданных функций:
x'=a(1-cos(t));
y'=a*sin(t).
Пределы интегрирования известны по условию - [0;2*Pi].
Запишем подинтегральную функцию за формулой x'*y-x*y' (поскольку кривая (циклоида) проходит за ходом часовой стрелки):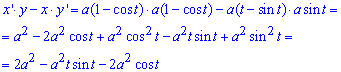 
Вычислим площадь фигуры ограниченной одною аркой циклоиды:
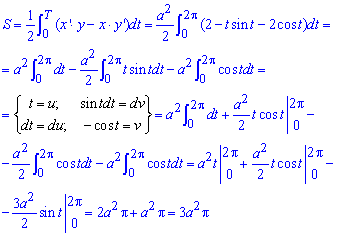
Определенные интегралы методом интегрирования частями вычисляются достаточно быстро.
Также не забывайте, что площадь измеряется в единицах квадратных.
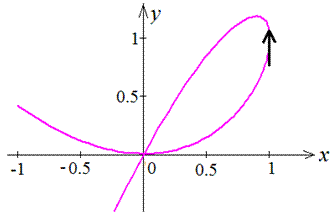
Пример 2.101 (2414) Вычислить площадь фигуры, которая ограничена параметрическими кривыми x=2t-t2, y=2t2-t3.
Вычисление: Вычислим производные по переменной t функций:
x'=2-2t;
y'=4t-3t2.
Найдем пределы интегрирования - точки пересечения кривой, которая ограничивает заданную фигуру:
x=0 при t1=0, t2=2 и
y=0 при t1=0, t2=2 .
Поэтому имеем период ровный T=2.
Запишем подинтегральную функцию по формуле x'*y-x*y' (поскольку кривая проходит против часовой стрелки):
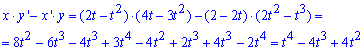
Вычислим площадь фигуры, которая ограничена заданной кривой:
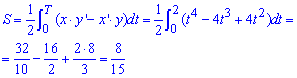
Здесь, как видите, интеграл найти вообще просто, подобные примеры на практических из математического анализа Вы возможно вычисляли огромное количество раз.
Пример 2.102 (2417.1) Найти площадь фигуры, которая ограничена параметрическими кривыми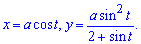 
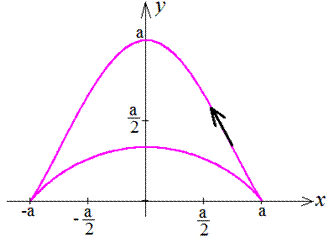
Вычисление: Продифференцируем функции по переменной t:
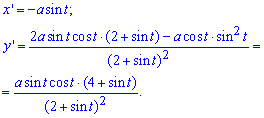
Запишем пределы интегрирования (нужно предварительно исследовать функцию):
T=[0;2*Pi].
Запишем подинтегральную функцию за формулой x'*y
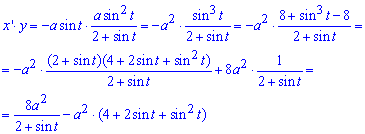
Вычислим площадь фигуры по формуле для параметрических кривых:
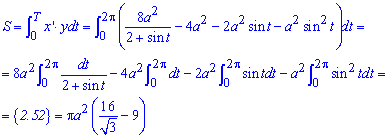
Определенный интеграл достаточно простой в плане вычислений.
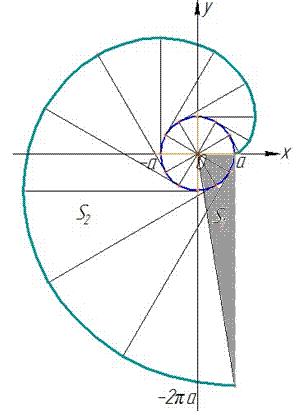
Пример 2.103 (2415) Найти площадь фигуры, ограниченной кривыми
x=a(cos(t)+t*sin(t)), y=a(sin(t)-t*cos(t)) (развертка круга) и x=a, 
.
Вычисление: Найдем производные функций по переменной t:
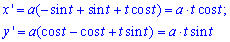
Пределы интегрирования выписываем из начального условия - [0;2*Pi].
Выведем подинтегральную функцию за формулой x'*y-x*y'
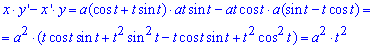
Вычислим площадь фигуры, которая ограничена заданной кривой и прямыми:
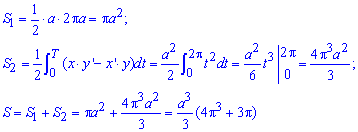
Следует заметить, что при интегрировании по углу не учитывается площадь треугольника S1, что заштрихована серым.
Без построения графика функции учесть необходимость находить дополнительную площадь достаточно трудно.
Пример 2.104 (2416) Найти площадь фигуры, ограниченной кривыми
x=a(2*cos(t)-cos(2t)), y=a(2*sin(t)-sin(2t)).
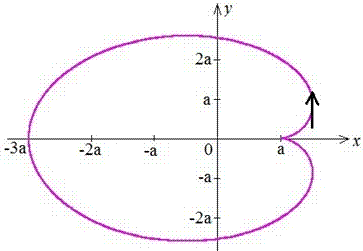
Вычисление: Вычислим производные по переменной t функций:
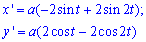
Запишем пределы интегрирования: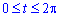 
Сложим уравнение подинтегральной функции по формуле x'*y-x*y'
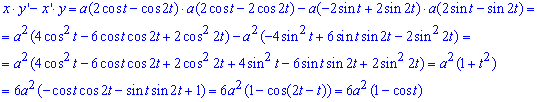
Через определенный интеграл вычисляем площадь фигуры, которая ограничена заданной кривой:
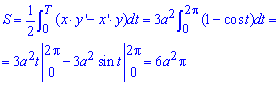
Интеграл не сложный, а конечная формула простая для расчетов площади.
Пример 2.105 (2417) Найти площадь фигуры, ограниченной параметрическими кривыми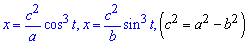 
(эволюта эллипса)
Вычисление: Эволюта - множество точек центров кривизны кривой.
По отношению к своей эволюте любая кривая является эвольвентой (інволютою, то есть разверткой этой кривой).
Найдем производные функций по переменной t :
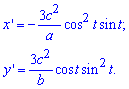
Пределы интегрирования равны:
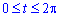
Запишем подинтегральную функцию по формуле
x'*y-x*y':
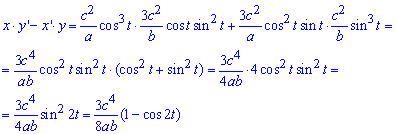
Интегрированием за периодом находим площадь фигуры, которая ограничена заданной кривой:
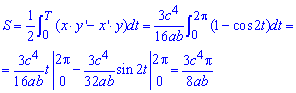
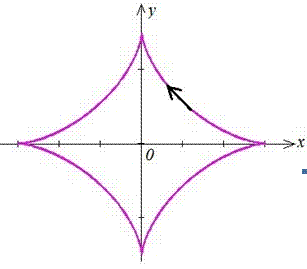
Пример 2429 Возведя уравнение к параметрическому виду, найти площади фигуры, ограниченной кривой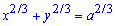
(астроида).
Вычисление: Перепишем уравнение астроиды в виде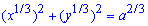 
Пусть x=a*cos3(t), y=a*sin3(t).
Нетрудно подставить и убедиться, что это именно та подстановка которая будет уравнением астроиды в параметрической форме.
Далее по аналогии с примером 2.105 будем иметь
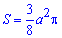
В следующих публикациях Вы найдете больше примеров на нахождение площади фигуры с помощью определенного интеграла.
