Якщо об'єм тіла V існує і функція S=S(x) є площею перерізу тіла площиною (визначена і гладка на проміжку [a;b]) , яка перпендикулярна до осі Ox в точці x, то об'єм тіла знаходиться за формулою
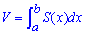Це досить проста залежність визначеного інтегралу, проблема полягає в тому, що функція площі не завжди виражається простою залежністю. В цьому Ви скоро переконається з розгляду готових відповідей на знаходження об'єму.
Приклади підібрано із програми для студентів мех-мату Львівського національного університету імені Івана Франка. Студенти решти міст України мають схожу програму навчання, завдання в ряді випадків співпадають.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:
Площа фігури а) Площа фігури, що обмежена кривими в прямокутних координатах; |
Довжина дуги а) Довжина дуги кривої в прямокутних координатах; |
Об'єм тіла а) Об'єм тіла за відомими поперечними перерізами; |
Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича).
Для вивчення методики знаходження об'єму тіл за відомими перерізами основні етапи інтегрування повторюватися з прикладу в приклад.
Знайти об'єми тіл, які обмежені наступними поверхнями
Приклад 2463 Знайти об'єм еліпсоїда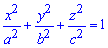 
Обчислення: Складемо рівняння підінтегральної функції. В перерізі тіла площиною, що перпендикулярна до осі Ox, отримаємо еліпс
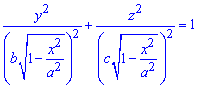
площа якого виражається функцією
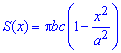
Визначимо межі інтегрування: у еліпсоїда в канонічній системі координат це проміжок [-a;a].
Знайдемо об'єм еліпсоїда:
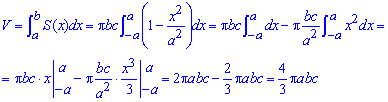
В тому що формула справедлива можете переконатися, порівнявши обчислену формулу з відомими в довідниках.
Об'єм фігур вимірюється в кубічних одиниць !
Бачимо, якщо еліпсоїд вироджується у сферу (a=b=c=R), то його об'єм рівний V=4/3*Pi*R3 (формула відома зі «шкільної» геометрії).
Приклад 2464 Знайти об'єм тіла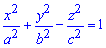 
(однополий гіперболоїд) 
.
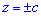Обчислення: Виразимо підінтегральну функцію. В перерізі тіла площиною, що перпендикулярна до осі Oz, отримаємо еліпс
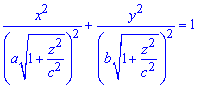
площа якого
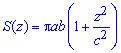
Межі інтегрування відомі за умовою: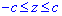 
.
Крім цього вони є підказкою в якому напрямку виконувати переріз і шукати функцію площі.
Знайдемо об'єм однополого гіперболоїда, що обмежений зверху і знизу площинами:
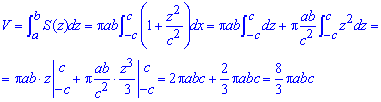
Визначений інтеграл в цьому завданні знаходиться без труднощів.
Приклад 2465 Знайти об'єм тіла утвореного перетином циліндричних поверхонь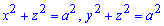
Обчислення: Складемо рівняння підінтегральної функції. Розглянемо 1/8 частину тіла (вона розташована в І квадранті).
В перерізі площиною, яка перпендикулярна до осі Oz, отримаємо квадрат, площа якого рівна
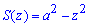
Межі інтегрування: І квадрат прямокутної системи координат [0;a].
Інтегруванням обчислюємо об'єм тіла:
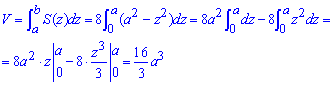
Як можна переконатися з формул площі, їх інтегрування доволі не складне.
Приклад 2468 Обчислити об'єм тіла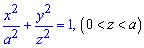 
Обчислення: Виразимо підінтегральну функцію. В перерізі площиною, яка перпендикулярна до осі Oz, отримаємо еліпс, площа якого відома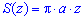
Межі інтегрування за умовою теж відомі: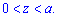 
.
Залишилося проінтегрувати і підставити межі.
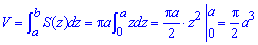
Отримали, що об'єм тіла рівний V=Pi/2*a3 куб. од.
Приклад 2469 Знайти об'єм тіла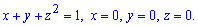 
Обчислення: Запишемо підінтегральну функцію. В перерізі площиною, яка перпендикулярна до осі Oz, отримаємо рівнобедрений прямокутний трикутник з катетом довжиною 1-z2, площа якого легко знаходиться
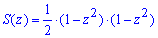
Межі інтегрування: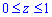 
(це видно із області існування функції 
).
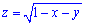Об'єм тіла знаходимо інтегруванням:
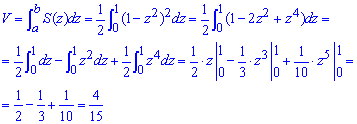
З наведених прикладів Ви могли зауважити, що все залежить від рівняння площі перерізу. Для того щоб його записати потрібно володіти доброю просторовою уявою та знати перерізи основних просторових тіл. Все решта залежить від Вашого вміння інтегрувати.
