Площа фігури обмеженої кривими в прямокутних координатах

Площа фігури між двома кривими в прямокутних координатах визначається інтегралом
від різниці кривих, де одна з них завжди приймає не менші значення ніж інша 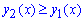, а також криві неперервні. Межі інтегрування - прямі x₁=a, x₂=b - обмежують фігуру, (a<b найчастіше це точки перетину заданих кривих).
Даний цикл задач в першу чергу підійде студентам мех-мату Львівського національного університету імені Івана Франка для проходження практикуму з математичного аналізу. Студенти інших ВУЗів можуть набиратися практики на таких інтегралах, та вивчати методику обчислення.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:

Перший номер в прикладах відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича).
Для запам'ятовування основних моментів схема інтегрування та знаходження площ з прикладу в приклад буде повторюватися. По можливості самі розв'язки будуть проілюстровані підінтегральними кривими.

Приклад 2.81 ( 2397). Знайти площу фігури, обмеженої кривими, заданими в прямокутних координатах ax=y², ay=x²,(a>0).

Обчислення: Запишемо графіки функцій, що обмежують шукану площу фігури: 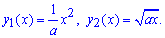На графіку вони матимуть наступний вигляд

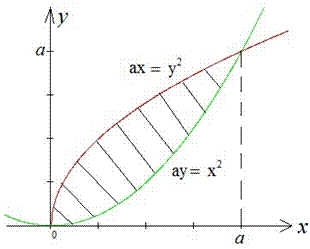
Площу між кривими і потрібно знайти. Як правило, Вам рідко буде відомо сам графік, тому в завданнях де не задано області на якій знаходити площу в першу чергу необхідно знайти точки перетину кривих.
Знайдемо межі інтегрування, тобто точки абсцис перетину заданих функцій y₁(x)=y₂(x):

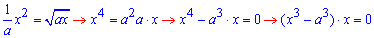
Як бачите такою умовою є умова рівності функцій.
З останнього рівняння отримаємо дві точки x₁=0, x₂=a. Далі, коли Ви не бачите графіка функцій необхідно встановити котра з кривих приймає більші значення. Це потрібно лише для того, щоб з першого разу отримати позитивне значення площі фігури. Оскільки площа завжди додатна, а інтеграл може приймати довільні значення, то без перевірки наступної умови для знаходження площі інтеграл потрібно брати за модулем.
Вибираємо довільну точку з відрізку інтегрування [0;a] і переконуємося у правильності нерівності 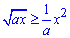, тобто перевіряємо котра з кривих приймає вищі значення 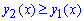. Як відзначалося вище, це потрібно для того, щоб після інтегрування отримати додатну площу фігури між кривими.
Обчислюємо площу фігури, що обмежена заданими кривими інтегруванням:

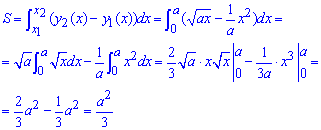
Тут ми мали доволі прості функції, тож звівши їх до табличних інтегралів знайти площу доволі легко. Наступні приклади міститимуть дедалі важчі функції, для інтегрування яких потрібно застосовувати знання практично усіх формул інтегрування.
Слід зауважити: значення площ (в усіх завданнях) вимірюються в квадратних одиницях (кв. од.), про це Ви повинні пам'ятати, однак для економії місця та часу тут будуть наведені лише значення визначених інтегралів.

Приклад 2.82 ( 2398). Обчислити площу фігури, обмеженої кривими y=x², x+y=2.
Обчислення: За методикою записуємо рівняння кривих, що обмежують площу фігури: y₁(x)=x², y₂(x)=2-x. Тут функції виразити доволі просто.
Обчислимо межі інтегрування, прирівнявши між собою функції y₁(x)=y₂(x):
x²=2-x.
Переносимо змінні по одну сторону від знаку рівності і розв'язуємо квадратне рівняння
x²+x-2=0;
(x+2)(x-1)=0.
Отже корені рівняння x₁=-2, x₂=1. Сам графік кривих та фігури, площу якої шукаємо, наведено на рисунку

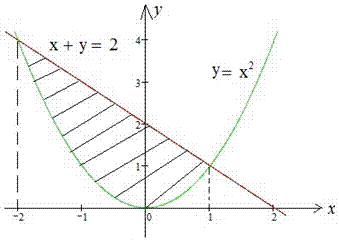
Підстановкою будь-якої точки з проміжку [-2;1], наприклад x=0 у функції переконуємося, що виконується нерівність 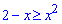, тому .
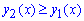Площа фігури обчислюємо інтегруванням різниці кривих у знайдених межах:

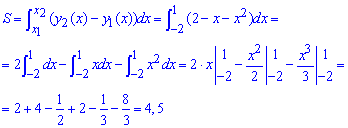
Площа рівна S=4,5 квадратних одиниць. За фізичним змістом площа фігури рівна різниці площ двох криволінійних трапецій. Перша відповідає за верхній графік y₂(x), нижня криволінійна трапеція за функцію, що приймає менші значення y₂(x). Різниця полягає в тому, що тут ще потрібно визначати межі інтегрування.

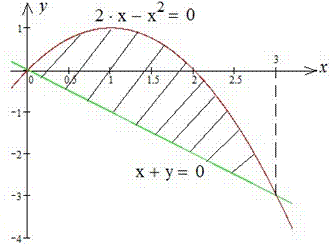
Приклад 2.83 ( 2399). Знайти площу фігури, обмеженої кривими y=2x-x², x+y=0.
Обчислення:Запишемо рівняння кривих, що обмежують шукану фігуру: y₁(x)=-x, y₂(x)=2x-x².
З умови рівності функцій y₁(x)=y₂(x) знайдемо границі інтегрування:
2x-x²=-x;
x²-3x=0;
x(x-3)=0.
Отже x₁=0, x₂=3.
Підстановкою одиниці бачимо, що на проміжку [0;3] справджується нерівність 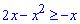, тобто .

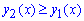Знаходимо площу фігури обмеженої заданими кривими:

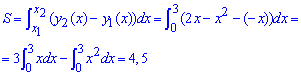
Під інтегралом проста квадратична функція, тому саме інтегрування не складне. Наступні функції дещо складніші в плані інтегрування, проте використовуючи табличні інтеграли площу знайти вдається.

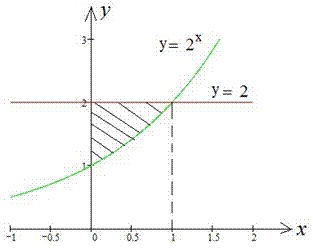
Приклад 2.84 (2400) Знайти площу фігури, обмеженої кривими y=2^x, y=2, x=0.
Обчислення: Запишемо підінтегральні функції: y₁(x)=2^x, y₂(x)=2, а також пряму x₁=0 (обмежує фігуру по осі абсцис).
Знайдемо другу границю інтегрування з умови рівності функцій y₁(x)=y₂(x):
2^x=2 , 2^x=2¹, звідси маємо другу точку x₁=1.
На проміжку [0;1] справджується нерівність 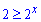, тому .
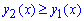Графіки степеневої функції та прямої наведено нижче.

Площа фігури, що обмежена кривими рівна інтегралу:

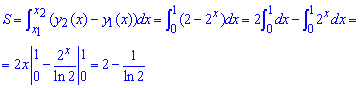
При інтегруванні отримаємо логарифм. На калькуляторах можете переконатися, що площа додатна.

Приклад 2.85 ( 2401) Обчислити площу фігури, обмеженої кривими y=x, y=x+sin²x , .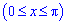

Обчислення: Запишемо рівняння кривих, що обмежують площу фігури: y₁(x)=x, y₂(x)=x+sin²x.
Далі межі інтегрування: x₁=0, x₂=Pi (це відомо нам за умовою).
На проміжку 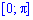справедлива нерівність 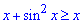, тому .

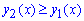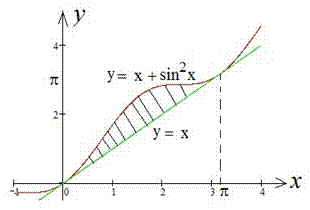
Якщо б існувала додаткова точка перетину, то площа була б рівна сумі двох інтегралів.
Площу фігури обчислюємо інтегруванням: квадрат синуса під інтегралом понижуємо та виражаємо за допомогою косинуса подвійного кута, а далі за класичною формулою інтегрування

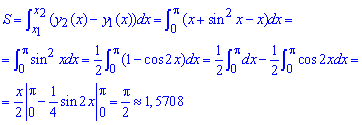
Площа рівна Pi/2, що приблизно рівно 1,5708.

Приклад 2.86 ( 2402) Знайти площу фігури, обмеженої кривими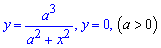
Обчислення: Переписуємо графіки функцій

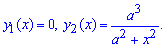
Знайдемо межі інтегрування, тобто точки абсцис перетину заданих функцій y₁(x)=y₂(x):
Оскільки функція парна

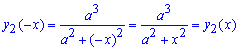
то знайдемо половину площі і результат помножимо на двійку;
З умови знаходимо

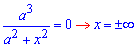
що межі рівні плюс, мінус безмежності. Щоб легше було уявити, що ми інтегруємо наведемо графік підінтегральних функцій

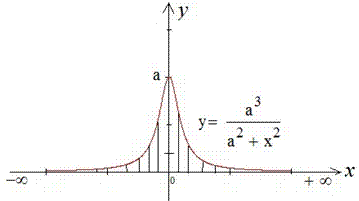
Враховуючи парність функції інтегрувати будемо від 0 до безмежності 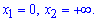, а отримане значення помножимо на двійку.
Отримаємо невластивий інтеграл першого роду (детальніше про нього у частині ІІІ).
Площу фігури обчислюємо через границю інтегралу:

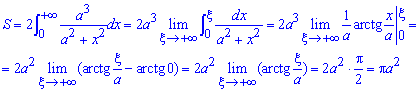
В результаті інтегрування отримаємо арктангенс, який в граничному випадку прямує до Pi/2.
Кінцева формула досить компактна та зручна для розрахунків, хоча з таким типом інтегралів Ви знайомитеся вперше.

Приклад 2.87 (2403) Обчислити площу фігури, обмеженої кривими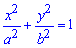
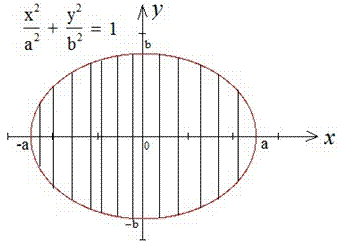
Обчислення: Всі Ви повинні знати, що такою формулою задається рівняння еліпса. Так як осі еліпса в канонічній системі координат є його осями симетрії, то ці осі ділять еліпс на 4 рівні частини. Тому розглядатимемо частину еліпса, що знаходиться в першому квадранті канонічної (прямокутної) системи координат. Виразимо рівняння функції, що обмежує шукану площу (четвертину еліпса):

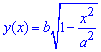
Запишемо межі інтегрування: з аналітичної геометрії відомо, що четверта частина еліпса обмежена x₁=0, x₂=a.

Для обчислення площі еліпса в самому інтегралі необхідно виконати заміну змінних, що в свою чергу веде до зміни меж інтегрування. При цьому прийдемо до квадрату косинуса, який понижуємо через косинус подвійного кута. В кінці маніпуляцій приходимо до табличних інтегралів, які легко інтегруємо та підставляємо межі:

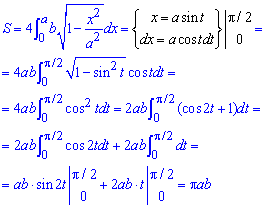
Отримали класичну формулу площі еліпса S=Pi*a*b .
Бачимо, якщо еліпс вироджується в коло при (a=b=R), тоді формула площі кола S=Pi*R².

Приклад 2.88 (2404) Обчислити площу фігури, обмеженої кривими y²=x²(a²-x²).
Обчислення: Так як усі змінні в заданому рівнянні входять у квадратах, то осі прямокутної системи координат є осями симетрії фігури, що обмежена цією лінією, тому ці осі ділять задану фігуру на 4 рівні частини. Достатньо розглянути частину фігури, що заходиться в першому квадранті прямокутної системи координат. Запишемо графік функції, що обмежує шукану площу четвертини фігури: .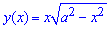
Графік невідомої фігури подібний на крила метелика.

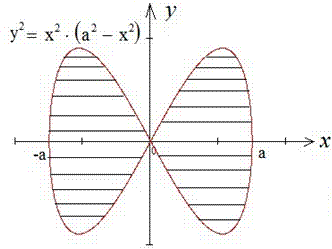
При y=0 маємо два корені рівняння x₁=0 і x₂=a. Площа фігури рівна 4 помножити на інтеграл із знайденими межами. Під час інтегрування виконуємо заміну змінних та меж інтегрування

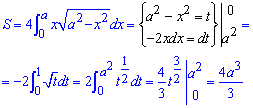
Це дозволяє перейти до показникової функції, яка легко інтегрується. Завжди пам'ятайте, що заміна змінних під інтегралом веде до зміни меж інтегрування.

Приклад 2.89 Знайти площу фігури, обмежену лініями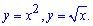
Обчислення: Запишемо графіки функцій, що обмежують шукану площу фігури: , .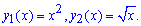
Визначимо межі інтегрування з умови y₁(x)=y₂(x):
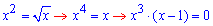отож x₁=0 і x₂=1.
Між функціями справедлива залежність 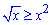на [0;1], тому 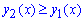. Графік функцій, що аналізуємо наступний

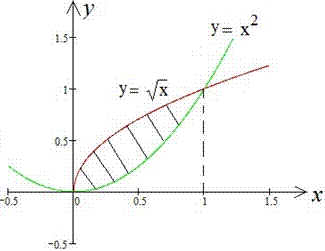
Площа фігури через визначений інтеграл рівна 1/3 (порівняйте 2.81 при a=1):

Приклад 2.90 Обчислити площу фігури, обмеженої кривими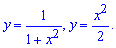
Обчислення: Обчислимо межі інтегрування з умови рівності функцій y₁(x)=y₂(x):

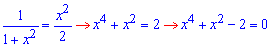
З біквадратного рівняння отримаємо значення точок перетину : x₁=-1 і x₂=1. Самі ж функції в прямокутних координатах матимуть вигляд

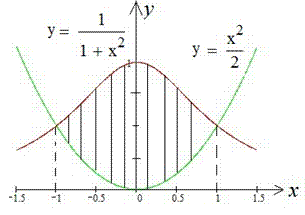
Інтегруванням знаходимо площу фігури (дивись рисунок і зразок 2.89) :

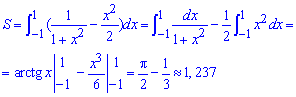
Перший інтеграл дасть арктангенс, запам'ятайте добре цю формулу.

Приклад 2.91 Обчислити площу фігури, обмеженої кривими y=e^x, y=e^-x,x=1.
Обчислення: З умови, яку Ви вже з повторюваності повинні вивчити y₁(x)=y₂(x) знаходимо точки перетину кривих:
e^x=e^-x,x=-x,2x=0, отже x₁=0. x₂=1 (відомо за умовою). Графік функцій наступний

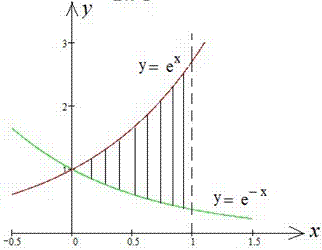
Експоненту інтегрувати не важко, а площа фігури виражається формулою (дивись рисунок і зразок 2.84) :

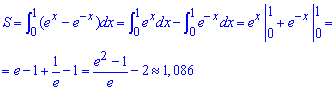
Приклад 2.92 Знайти площу фігури, обмеженої кривими y=ln(x), y=ln²(x).
Обчислення: Межі інтегрування з умови рівності функцій y=ln(x), y=ln²(x) рівні x₁=1 і x₂=e.

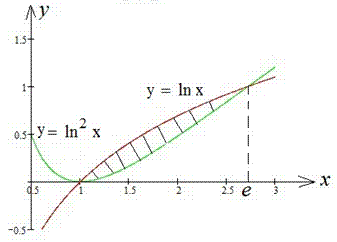
Інтегруванням логарифмів знаходимо площу фігури (дивись рисунок) :

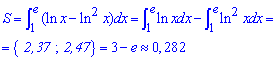
Тут треба проінтегрувати по частинах, поклавши ln(x)=u (ln²(x)=u) і dx=dv. Спробуйте проміжні викладки провести самостійно.

Приклад 2.93 Обчислити площу фігури, обмеженої кривими y=ln(x), y=ln(a), y=ln(b), x=0, де 0<a<b.
Обчислення: Запишемо графіки функцій, що обмежують шукану площу фігури: x(y)=e^y (тобто обернена функція до заданої функції y(x)=ln(x)) . Такий прийом застосовують, коли межі інтегрування паралельні осі Оx, тобто y=const.
Запишемо межі інтегрування: y₁=ln(a),y₂=ln(b) (відомо за умовою).
Графік шуканої фігури наступний

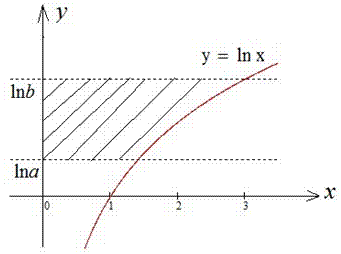
Площа фігури, що обмежена заданими кривими:

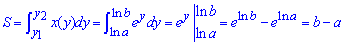
Приклад 2.94 Знайти площу фігури, обмеженої кривими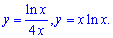
Обчислення: Межі інтегрування в формулі площі знаходимо з умови y₁(x)=y₂(x):
ln(x)/(4x)=x*ln(x).
Спростивши на логарифм (якщо він більший нуля), отримаємо
1=4x²; 4x²-1=0, x₁=1/2.
З умови на логарифм (=0) отримаємо
ln(x)=0; x₂=1. ОДЗ: x>0.
Графік фігури в прямокутних координатах наступний

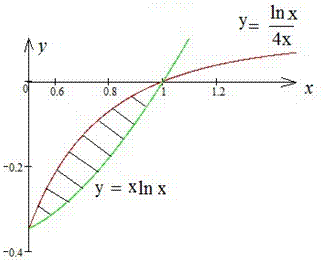
Площа фігури між кривими (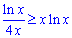 на [0,5;1]) знаходимо інтегруванням: для обчислення інтегралів використовуємо метод заміни змінних

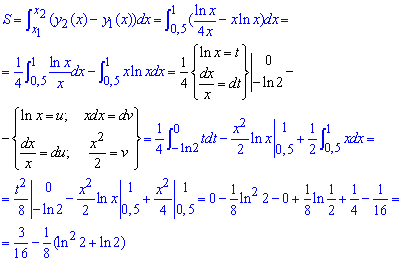
Обчислення не з простих, тому з перетвореннями спробуйте розібратися самостійно.

Приклад 2.95 Обчислити площу фігури, обмеженої кривими y=arcsin(x), y=arccos(x), y=0.
Обчислення: Знаходимо точки перетину кривих з рівності x₁(y)=x₂(y):
sin(x)=cos(y), звідси y₁=0 (відомо за умовою) і y₁=Pi/4 (зразок 2.93). На графіку це виглядає наступним чином

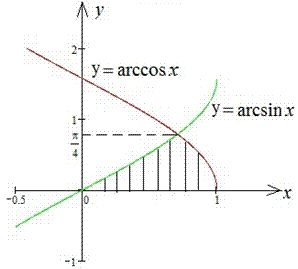
Враховуючи справедливість нерівності 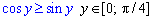обчислюємо площу фігури:

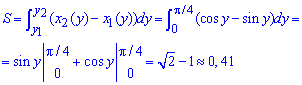
Думаю, що з такими завданнями на екзамені чи модулях Ви справитеся.

Приклад 2.96 Знайти площу фігури, обмеженої кривими y=tg(x) , y=2/3*cos(x), x=0.
Обчислення: Знайдемо межі інтегрування, тобто точки абсцис перетину заданих функцій y₁(x)=y₂(x):
tg(x)=2/3*cos(x), звідси 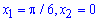(друга відома за умовою).
Криві на площині мають вигляд

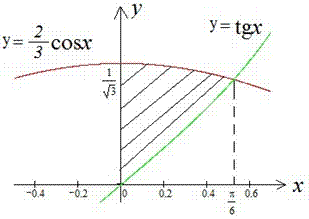
Площа фігури, що обмежена заданими кривими () рівна інтегралу:

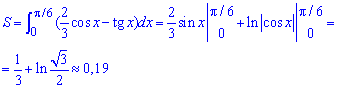
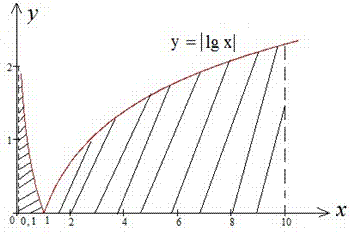
Приклад 2.97 (2400) Обчислити площу фігури, обмеженої кривими y=|ln(x)|, y=0, x=0,1; x=10.
Обчислення:Виписуємо межі інтегрування x₁=0,1; x₂=10 з початкової умови. Як будувати модуль від логарифма Ви, мабуть, ще не забули

Площа фігури рівна сумі двох інтегралів, причому перший беремо зі знаком мінус ():

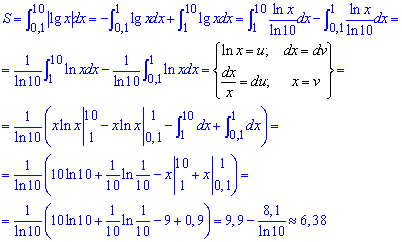
Під час інтегрування використовували інтегрування частинами.

Приклад 2.98 (2400) Знайти площу фігури, обмеженої кривими y=(x+1)² , x=sin(Pi*y), y=0, .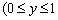
Обчислення: Запишемо графіки функцій, що обмежують шукану площу фігури: 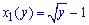(тут взяли обернену функцію до заданої y₁(x)=(x+1)² ), x₂=sin(Pi*y).
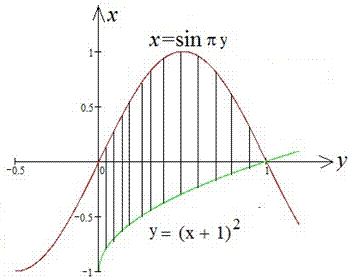
Випишемо межі інтегрування: y₁=0; y₂=1 (відомо за умовою). Графік функцій наведено нижче

Невідому площу фігури обчислюємо інтегруванням ():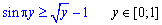

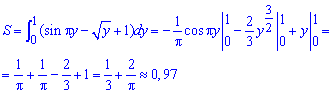
Приклад 2.99 Обчислити площу фігури, обмеженої кривими y=sin(x) , y=cos(x), y=0,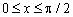
Обчислення: З рисунку видно, що площу S краще розбити на дві частини: S=S₁+S₂.

Запишемо графіки функцій, що обмежують шукану площу фігури:


Інтегруємо синус та косинус функції та знаходимо шукану площу
.
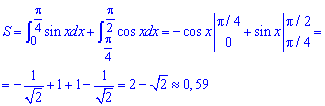
Інший варіант полягає у інтегруванні різниці обернених функцій по y.

Приклад 2407 Знайти площу фігури, обмеженої кривими 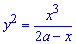(цисоїда Діокла), x=2a, (a>0).
Обчислення: Оскільки графік функції 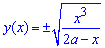симетричний відносно осі Ox, то будемо розглядати половину площі фігури (над віссю Ox) і результат помножимо на 2. В точці x=2a функція не визначена, тому матимемо інтеграл другого роду (детальніше дивіться частину ІІІ), він є збіжним і тому площа буде виражена числом. Запишемо межі інтегрування: x₁=0 (бо 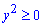), x₂=2a (за умовою). Графік функцій наступний

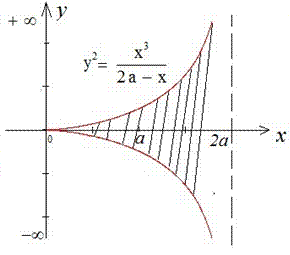
Площа фігури, що обмежена заданою кривою знаходиться доволі непростим інтегруванням



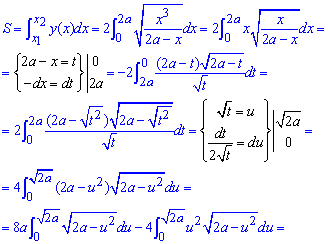
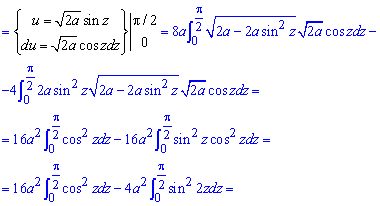
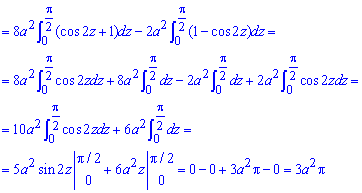
Тут довелося тричі виконувати заміну змінних, щоб добратися до правильної відповіді.
Ще раз уважно розберіть інтеграл.

Приклад 2408 Обчислити площу фігури, обмеженої кривими 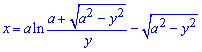(трактриса), y=0.
Обчислення: Трактриса – крива, по якій рухається об'єкт, коли його тягнути по горизонтальній площині за мотузку фіксованої довжини, якщо напрямок руху тягача є ортогональним до початкового положення мотузки та швидкість тягача нескінченно мала величина.
Очевидно, що (дивись рисунок).

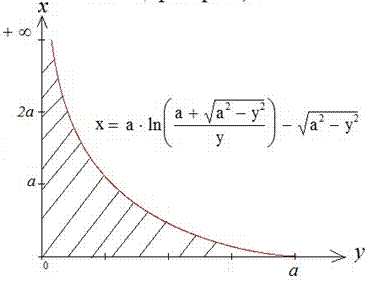
Приймаючи до уваги, що додатному приросту x відповідає від'ємний приріст y, і що фігура не квадрована (в загальному розумінні), допускаємо

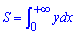
де диференціал за x знаходимо через похідну

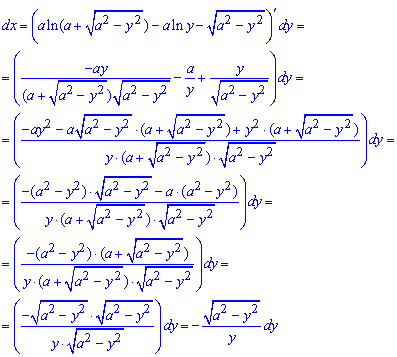
Отож, площа фігури через визначений інтеграл рівна

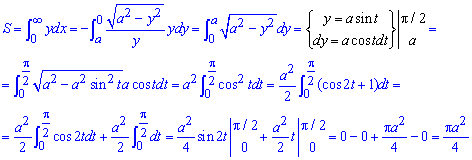
Кінцева формула досить проста для обчислень площі.
На цьому, поки що все. Наступним іде матеріал з якого Ви навчитеся знаходити площу фігури, що обмежена кривими заданими параметрично.