Приклади на інтегрування функцій взято з матеріалів контрольної роботи, яку задають студентам 1, 2 курсів математичних факультетів. Для економії Вашого часу самі умови завдань пропущені, всюди потрібно або "Знайти неозначений інтеграл" або "Обчислити інтеграл". Тексту в коментарях до кожного завдання рівно стільки, скільки потрібно Вам для засвоєння матеріалу і вивчення методики та схем інтегрування.
Інтегрування частинами
Приклад 8. Тут необхідно інтегрувати частинами. Хто не знає як інтегрувати часинами, то спершу ознайомтеся з цією статтею. За dv зручно обрати експоненту помножену на dx. Обчислюємо v, du та застосовуємо інтегрування частинами
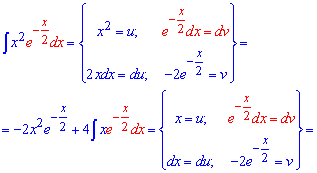
До другого інтегралу повторно застосовуємо правило інтегрування частинами
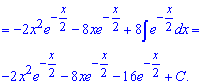
Якщо би мали змінну в 3-му степені то інтегрували б частинами тричі і т.д. Іншого методу обчислити такого сорту інтеграли математики ще не придумали.
Приклад 9. В цьому інтегралі за dv можемо позначати як експоненту так і синус, оскільки його друга похідна теж дасть синус (зі знаком мінус). В кожному із випадків прийдемо до рекурентної формули з якої і знайдемо інтеграл
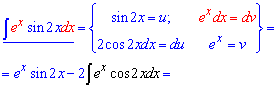
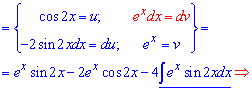
Прийшли до рекурентної формули, коли справа і зліва від знаку рівності маємо шуканий інтеграл
![]()
Групуємо доданки та ділимо праву сторону на коефіцієнт при інтегралі
![]()
Приклад 10. Незважаючи на короткий запис, інтеграл від арксинуса подвійного «ікс» потрібно знаходити інтегруванням частинами. Функції u, dv вибираємо за поданими формулами
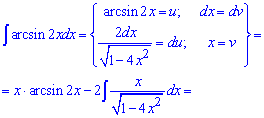
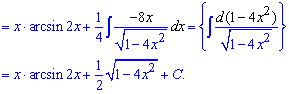
Останні два рядки можна розписати переходом до нової змінної, а потім її підставленням в інтеграл, однак і такий запис буде правильним та змістовним для Вас.
Приклад 11. Знаходимо інтеграл частинами, для цього прямо застосовуємо метод. Тут в дужках виконуємо спрощення в обчисленнях диференціалу du
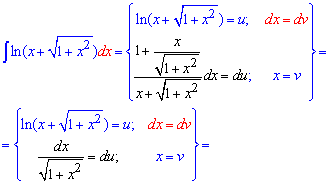
Для застосування формули інтегрування вносимо змінну під диференціал, щоб отримати такий самий вираз, як під коренем
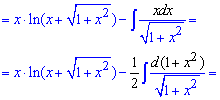
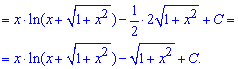
Поступово Ви запам'ятаєте, що внесення під диференціал дозволяє опускати заміни змінних і зразу переходити до готових формул на інтеграли.
Інтеграли, що містять квадратні тричлени
Приклад 12. Маємо квадратний тричлен в знаменнику дробу. Для зведення до табличного інтегралу слід його звести то різниці або суми квадратів. В заданому випадку отримаємо арктангенс
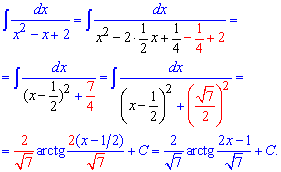
Для легкості читання формул важливі моменти виділені кольором. Повірте, що це допомагає в рази швидше запам'ятати те, що на перший погляд виглядає одним зрозумілим, а іншим і після другого та третього перегляду важким.
Приклад 13. Незважаючи на те, що квадратний тричлен в знаменнику міститься під коренем схема зведення до табличного інтегралу подібна до попереднього прикладу. Різниця лиш в тому, що тут отримаємо логарифм, а не арктангенс. Важливі моменти перетворень записано формулами
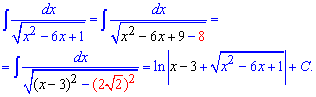
Завдання типу 12, 13 на контрольних та тестах зустрічаються часто, тож добре їх запам'ятайте.
Приклад 14. В цьому інтегралі заміна змінних дещо специфічна і навряд чи Ви її завчите, однак без неї інтеграл не знайти. Тож уважно розгляньте, як перетворюється функція під інтегралом при такій заміні змінних
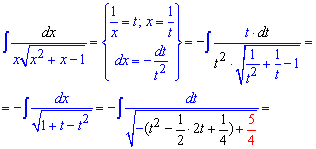
Під коренем в знаменнику виділяємо різницю квадратів. Оскільки перед дужками, що містять змінну стоїть від'ємний знак то при інтегруванні отримаємо арксинус
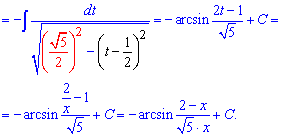
Решта відповідей в наступних матеріалах. Пам'ятайте, що такого роду приклади задають на контрольній чи тестах та уважно розбирайте відповіді до завдань.
Готові розв'язки контрольної з інтегрування


