Приклади на інтегрування функцій взято з матеріалів контрольної роботи, яку задають студентам 1, 2 курсів математичних факультетів. Для економії Вашого часу самі умови завдань пропущені, всюди потрібно або "Знайти неозначений інтеграл" або "Обчислити інтеграл". Тексту в коментарях до кожного завдання рівно стільки, скільки потрібно Вам для засвоєння матеріалу і вивчення методики та схем інтегрування.
Інтегрування раціональних дробів
Приклад 15. Спершу розкладаємо знаменник на прості множники
![]()
В результаті функція під інтеграл зведеться до найпростіших дробів з невідомими сталими.
![]()
Для їх обчислення зводимо доданки під спільний знаменник
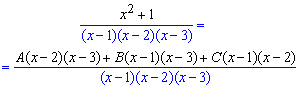
При рівних знаменниках розписуємо та прирівнюємо коефіцієнти при однакових степенях "ікс" по обидві сторони знаку рівності.
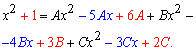
В результаті отримаємо систему лінійних алгебраїчних рівнянь (СЛАР) для обчислення сталих A, B, C
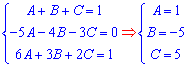
Розв'язок СЛАР можете знаходити методом Крамера, якщо більшість коефіцієнтів ненульові, або методом Гауса в протилежному випадку. При відомих сталих переходимо до інтегрування.
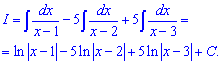
Приклад 16. Знаменник дробу розкладаємо на прості дроби. Один з коренів знаходимо серед дільників вільного члена (4={4;-4;2;-2;1;-1}).
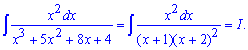
Розкладаємо дріб на доданки з невідомими сталими
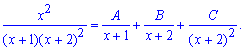
Далі зводимо під спільний знаменник
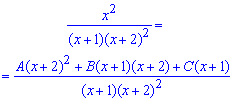
та після розкриття дужок у чисельнику, групуємо доданки
![]()
Далі складаємо систему рівнянь і обчислюємо коефіцієнти
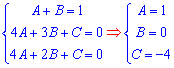
Сталі підставляємо у інтеграл та знаходимо його значення
![]()
Методика зведення під табличні інтеграли
Приклад 17. В даному завданні необхідно в чисельнику дробової функції виділити множник, який отримаємо при розписі знаменника до різниці чи суми квадратів. Далі його вносимо під диференціал та інтегруємо
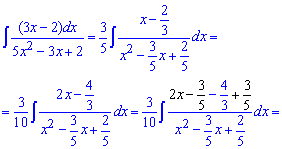
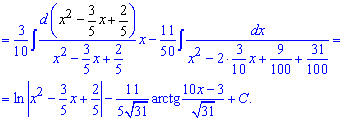
Тут пропущено перехід від останнього інтегралу до арктангенсу, тому спробуйте виконати перетворення самостійно. Практична робота нікому ще не пошкодила, а багатьох навіть змінила в кращу сторону.
Приклад 18. Щоб позбутися ірраціональності в чисельнику введемо степеневу заміну змінних. При цьому інтеграл розкладеться на два доданки, які мають простий для інтегрування вигляд
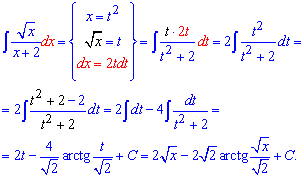
Якщо подивитися на відповідь, то все ніби просто і зрозуміло але як тільки доводиться мати справу з подібним завданням зразу руки опускаються і всі знання кудись зникають. Щоб такого не було розв'язуйте аналогічні прилади самостійно. Їх можете придумати на основі цього, або пошукати наприклад в Демидовича. Приклад 19. В знаменнику маємо ірраціональну функцію, тому щоб від цього позбутися за нову змінну вибираємо таку, щоб при її підстановці не мати коренів. В результаті заміни інтеграл зведеться до табличних формул
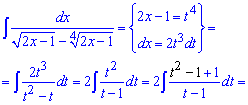
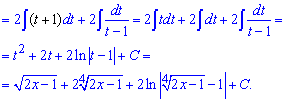
Після інтегрування повертаємося до виконаної заміни.
Решта відповідей в наступних матеріалах. Пам'ятайте, що такого роду приклади задають на контрольній чи тестах та уважно розбирайте відповіді до завдань.
Готові розв'язки контрольної з інтегрування


