Приклади на інтегрування функцій взято з матеріалів контрольної роботи, яку задають студентам 1, 2 курсів математичних факультетів. Для економії Вашого часу самі умови завдань пропущені, всюди потрібно або "Знайти неозначений інтеграл" або "Обчислити інтеграл". Тексту в коментарях до кожного завдання рівно стільки, скільки потрібно Вам для засвоєння матеріалу і вивчення методики та схем інтегрування.
Приклад 1. При інтегруванні дробової функції необхідно в знаменнику корінь квадратний перетворити на показник, далі розділити чисельник на знаменник і отримані доданки проінтегрувати. Якщо не вдаватися в дрібні розписування то в кінцевому варіанті інтеграл прийме значення
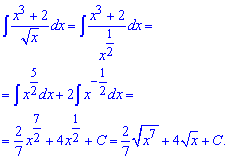
Для більшості студентів хід обчислень має бути зрозумілим, якщо перехід між останніми двома рядками Ви не можете здійснити то почніть з того, що відкрийте або роздрукуйте основні формули інтегрування.
Приклад 2. Маємо під інтегралом дріб від синус функцій, спершу спрощуємо діленням чисельника на знаменник. Далі знаменник дробу в другому інтегралі розписуємо за теоремою косинуса, а синус вносимо під диференціал. Таким чином перейдемо до нової змінної t=cos(x) в інтегруванні.
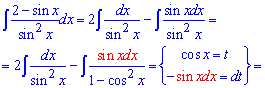
Другий інтеграл за табличними формулами рівний логарифму від частки простих множників знаменника
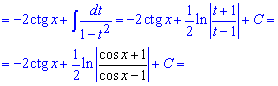
Повертаємося до заміни, яку виконували. На цьому інтегрування можна було і завершити, а можна записати в компактнішому вигляді. Але для цього необхідно знати або мати під рукою тригонометричні формули та властивості логарифма.
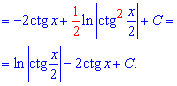
Приклад 3. Для обчислення інтегралу запишемо знаменник дробу у вигляді різниці квадратів, а далі помножимо на мінус одиницю та зведемо до табличного логарифма від частки простих множників
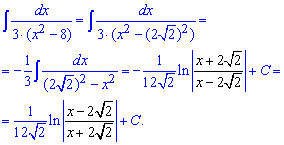
Мінус перед логарифмом загнали в показник функції, тому дріб під логарифмом в кінцевому варіанті обернутий.
Приклад 4. Дуже повчальне завдання на інтегрування, побільше би таких на контрольних чи тестах. Якщо б в степені мали 3 чи 4, то підносити ще хоч якось було б можна. Тут же стоїть 10, тому підносити до 10 степеня мало хто захоче. Для спрощення вираз в дужках в подібних завданнях на інтегрування позначте за нову змінну t=2x+5. Далі застосовуємо табличну формулу і після того, як проінтегрували не забуваємо підставити заміну.
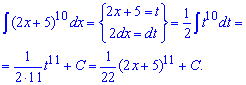
Добре запам'ятайте схему обчислення цього інтегралу.
Приклад 5. На перший погляд складний інтеграл, однак схема обчислень достатньо проста. Позначимо арккосинус за нову змінну t=arccos(x) та запишемо її диференціал. Як бачите диференціал рівний dx розділити на знаменник. І така схема більшості складних прикладів на неозначені інтеграли. Тому Ваше основне завдання – навчитися бачити заміни змінних, схеми зведення під табличну формулу, вдало вибирати функцію під правило інтегрування частинами. А для цього потрібно розв'язати чимало інтегралів, тож краще вчитися на готових відповідях+самосійна робота.
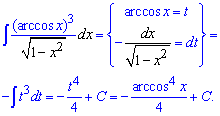
Приклад 6. Під інтегралом маємо дробову ірраціональну функцію від експоненти. Для обчислення інтегралу позначимо функцію під коренем за нову змінну. Також перетворимо експоненту в чисельнику та знайдемо диференціал від нової змінної.
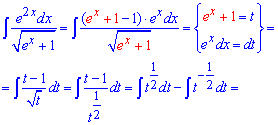
Після таких дій отриманий інтеграл за складністю нічим не поступатиметься першому з розглянутих прикладів. Після інтегрування не забуваємо повернутися до виконаної заміни змінних.
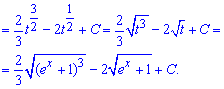
Приклад 7. Для обчислення цього та інших прикладів Ви повинні знати, що похідна від логарифма рівна одиниці розділеній на змінну. Таким чином більшості інтегралів де міститься показникові функція від логарифма та «ікс» в знаменнику за нову змінну вибирайте логарифм t=ln(x). В результаті інтеграл суттєво спростися і отримаємо компактний результат
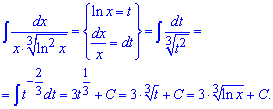
Решта відповідей в наступних матеріалах. Пам'ятайте, що такого роду приклади задають на контрольній чи тестах та уважно розбирайте відповіді до завдань.
Готові розв'язки контрольної з інтегрування


