Із формули диференціала добутку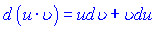 
інтегруванням двох частин рівності одержуємо формулу інтегрування частинами
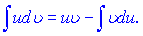
За цією формулою знаходження інтеграла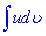 
зводиться до знаходження іншого інтеграла 
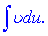Застосовувати цю формулу потрібно в тих випадках, коли інтеграл 
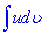легко знаходитися. Якщо неправильно вибрати 
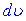, то завдання навпаки може ускладнитись. Для застосування формули інтегрування частинами до інтегралу 
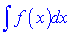необхідно підінтегральний вираз 
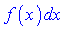представити в вигляді добутку двох множників 
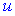та 
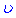. За диференціал 
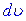завжди вибирають такий вираз, що містить 
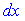. Його інтегруванням можна знайти 
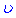. За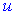 
в більшості випадків приймається функція, яка при диференціюванні спрощується.
В такий спосіб на перший погляд важкі і незрозумілі, з точки зору обчислень, інтеграли можна швидко звести до табличного вигляду.
Поширені приклади інтегрування частинами
Приклад 1. Обчислити невизначені інтеграли методом інтегрування частинами.
а) якщо на практиці Ви зустрінете добуток полінома на синус чи косинус, то останні і слід вносити під диференціал
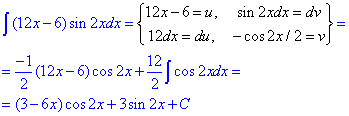
б) Перший раз арктангенс залишаємо, а за dv позначаємо dx. Далі обчислюємо похідну арктангенса та підставляємо.
подальші заміни для інтегрування частинами розбирайте самостійно з формули
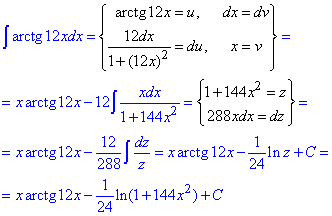
Приклад 2. Обчислити інтеграли
а)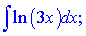 
Розв'язок: Даний інтеграл один з класичних в курсі вищої математики. Функції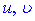 
підбираємо таким чином
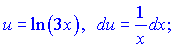
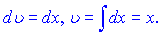
Згідно формул інтегрування частинами маємо
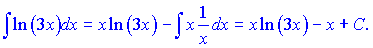
б)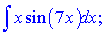 
Розв'язок: Для даного інтеграла функції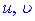 
для підстановки вибираємо у вигляді
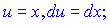
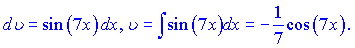
За формулою отримаємо
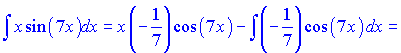
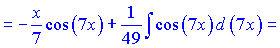
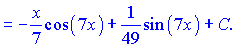
На цьому прикладі добре видно ефективність методу підстановки. Ніяка інша методика не дозволяє так швидко обчислити інтеграл.
в)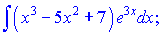 
Розв'язок: Для заданого заміни вибираємо наступними
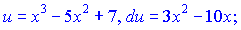
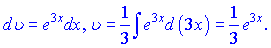
Підставляємо в інтеграл та обчислюємо його
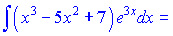
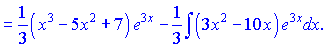
Бачимо, що знову отримали інтеграл до якого потрібно застосувати правило інтегрування частинами. За схемою вибираємо функцію
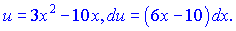
Формли для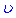 
беремо з попереднього інтегрування. Підставляємо в інтеграл та знаходимо
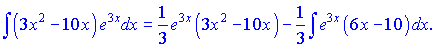
Останній доданок потребує повторного інтегрування частинами. Для цього записуємо заміну змінних
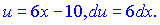
Друга змінна залишається без змін. Залишився один крок до повного обчислення значення інтегралу.
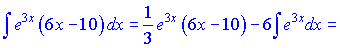
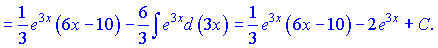
Всі внутрішні інтеграли підставляємо у початкову формулу
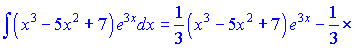
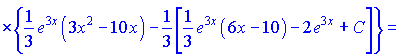
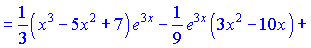
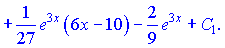
Це і є відповіддю до завдання.
г) 
Розв'язок: Вибираємо функції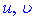 
для застосування правила заміни змінних у вигляді
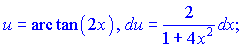
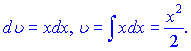
За правилами інтегрування отримаємо
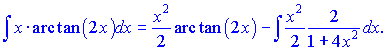
Останній інтеграл знайдемо за правилом розкладу, для цього чисельник доповнюємо до вигляду знаменника
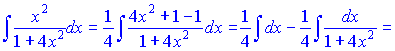
Остаточно інтеграл матиме вигляд
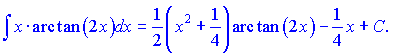
д)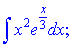 
Розв'язок: За функції u,v вибираємо наступні
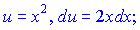
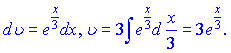
За правилом інтегрування частинами знаходимо неозначений інтеграл
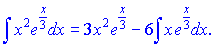
Для останнього доданку необхідно повторно застосувати інтегрування частинами.
Першу функцію вибираємо так
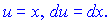
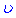- залишається без змін. Обчислюємо інтеграл
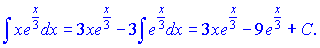
Значення інтегралу підставимо в попередній вираз
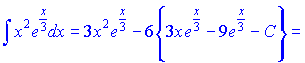
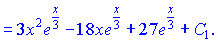
В цьому завдання застосовувати правило доводилося повторно. Це не складно, адже Ви тепер знаєте, яку робити заміну змінних при інтегруванні частинами.
е) 
Розв'язок:Вибираємо функції u,v для заміни змінних наступними
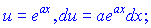
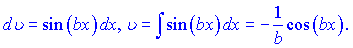
Здійснимо інтегрування частинами
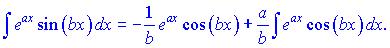
Далі u залишаємо без змін, а v знаходимо інтегруванням
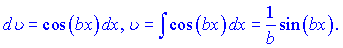
Повторно інтегруємо косинус
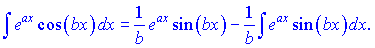
Необхідно зауважити, що шуканий інтеграл та останній однакові. Позначимо їх
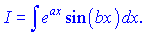
При цьому отримуємо рекурентну залежність
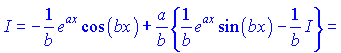
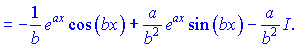
З рівняння виражаємо невідомий інтеграл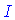
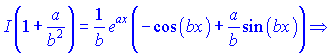
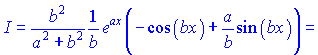
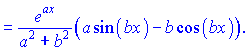
Інтеграли на подобі останнього зустрічаються доволі рідко, проте вимагають особливої уваги при їх розв'язанні. Найменша помилка може призвести до ускладнення інтегралу і красивого рівняння Ви можете не отримати. Тому будьте уважні при обчисленнях.
Сподіваюсь, що з даного уроку Ви багато потрібного для себе почерпнули. Практикуйте в розв'язуванні задач і до зустрічі в наступних уроках.
