Сьогодні будемо застосовувати попередній досвід зі знання методів розкладу, заміни змінних та інтегрування частинами до неозначених інтегралів. Паралельно з тим вчимося обчислювати інтеграли в математичному пакеті Maple. Щоб не дублювати "Знайти інтеграл", "обчислити інтеграл.." і т.д.
Замість інтегралу, що потрібно знайти, в умові наведемо код в Maple для розрахунку неозначеного інтегралу.
В такий спосіб швидше охопимо більше матеріалу.
Приклад 1. int(ln(x),x);
Щоб знайти інтеграл від логарифма проінтегруємо частинами
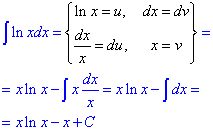
Результат з Мейплу наведемо нижче, а Ви вже звіряйте чи співпали чи ні. В будь-якому випадку вони вірні, тільки підхід до обчислень може бути інший.
Приклад 2. int(1/cos(x), x);
Щодо універсальних способів інтегрування тригонометричних функцій, то методик і алгоритмів тут безліч. А все тому, що є безліч формул запису тої самої тригонометричної ф-ї через інші. Це може як ускладнити обчислення, так і значно спростити їх.
Тут в штучний спосіб перетворили дріб та заміною змінних звели до інтеграла дробової функції, який рівний логарифму
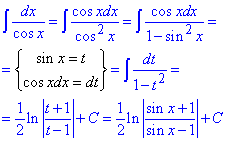
В мат. пакеті закладений свій алгоритм, тому результат відрізняється (див. нижче)
Приклад 3. int(x*exp(-x), x);
Майже усі інтеграли, в яких функція під інтегралом має множником експоненту знаходять інтегруванням частинами
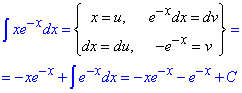
Приклад 4. int(1/(1-co(x)), x);
Замінимо косинус за тригонометричною формулою через синиус в квадраті половини кута, а далі при інтегруванні отримаємо котангенс

Приклад 5. int(1/(1+x)/sqrt(x), x);
Вносимо змінну під диференціал, попередньо перетворивши підінтегральну функцію
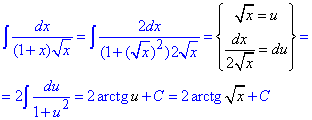
В дужках наведений номер в збірнику задач Б. П. Демидовича
Приклад 6 (1670). int(1/(1+sin(x)), x);
Використаємо наступний спосіб обчислення такого виду інтегралів
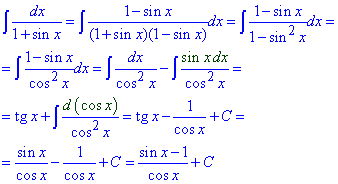
або скористаємося періодичністю синуса та позбудемося одиниці в знаменнику
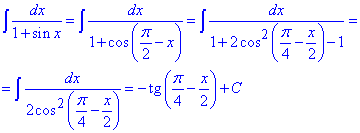
Приклад 7 (1748) int(cos(x)^3, x);
Виконуємо обчислення, застосовуючи основну тригонометричну тотожність та вносячи косинус під диференціал

Приклад 8 (1768). int(x^2/sqrt(2-x), x);
Тут щоб знайти інтеграл застосовуємо заміну змінних.
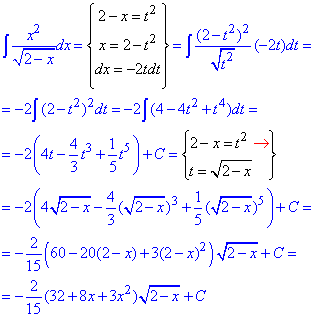
Вкінці не забувайте виконувати зворотну заміну змінних.
Приклад 9. int(sin(x)^3, x);
Інтеграл від синуса в кубі шукаємо аналогічно до 2, 7 прикладів
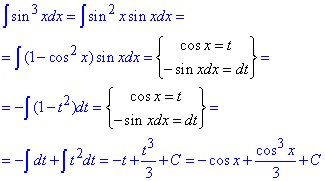
Приклад 10. int(x^2*(-x+1)^(1/3), x);
Інтеграли з коренями такого виду обчислюють заміною змінних, таким чином при розписанні отримують многочлен, а його інтегрувати не важко.
Вкінці виконуємо зворотну заміну та розкриваючи дужки, сумуємо подібні доданки
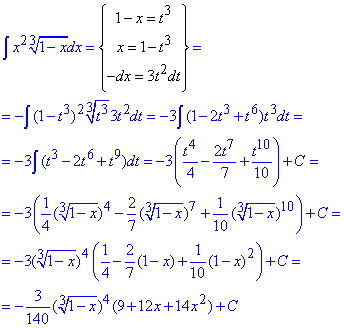
В мейплі всіх переходів Ви не отримаєте, зате кінцева відповідь, на відміну від отриманої ручним численням, точно буде правильною, а також інформативною для усіх, хто хоче навчитися чогось нового.
Плюс - Ви побачите кінцевий результат, що теж є підказкою як обчислювати інтеграл.

Відповідний файл з інтегралами з Maple ви можете завантажити та використовувати в навчанні.
Пізніше навчимо Вас обчислювати в Мейпл визначені, подвійні та потрійні інтеграли.
Серед онлайн сервісів для обчислення інтегралів заслуговує увагу wolfram alpha за адресою
https://www.wolframalpha.com/calculators/integral-calculator/
Для прикладу, щоб знайти 10 інтеграл, достатньо в поле ввести функцію з коду Мейпла та натиснути знак "дорівнює".
В результаті отримаємо
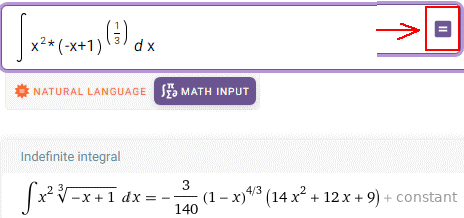
На контрольних чи розрахункових це добрий помічник.
Якщо потрібна повна відповідь, тоді вчіться інтегрувати самостійно. В крайніх випадках можете звертатися за допомогою до нас.
На сусідніх сторінках сайту ще багато готових інтегралів, тож вчитися є з чого, головне знайти час та мати бажання самостійно розібратися з методами інтегрування, на яких наголошуємо у формулах.


