Контрольну роботу на інтегрування подібного складу завдань задають студентам 1, 2 курсів. Це здебільшого завдання для математиків, економістів, статистів, програмістів. Дані приклади задавали на контрольній роботі в ЛНУ ім. І. Франка, "Львівська Політехніка", КНЕУ також практикує подібні контрольні з інтегрування.
Щоб формули в завданнях і відповідях не повторювалися самі завдання описувати не будемо. Всім і так відомо, що в завданнях потрібно або "Знайти інтеграл" , або "Обчислити інтеграл".
Приклад 1. Потрібно знайти інтеграл від дробової ірраціональної функції. Для цього спершу корені перетворимо на показники
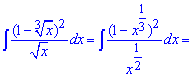
Далі в чисельнику підносимо дужку до квадрату. Залишається поділити чисельник на знаменник та за правилом суми про інтегрувати кожен із доданків.
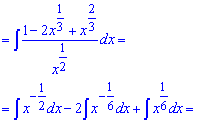
В результаті інтеграл прийме значення
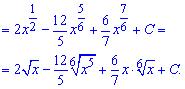
Приклад 2. Обчислюємо інтеграл від добутку показникової функції на експоненту. Для цього обидва множники вносимо під спільний степінь та застосовуємо формули інтегрування
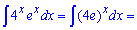
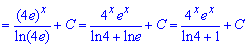
Приклад 3. Для знаходження інтегралу під коренем виконаємо такі перетворення, які б дозволили отримати при змінній коефіцієнт одиницю. Це зручно для прямого застосування табличної формули
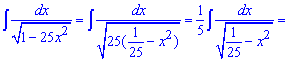
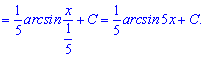
Оскільки маємо справу з неозначеними інтегралами, то слід не забувати додати вкінці сталу.
Приклад 4. Для обчислення інтегралу позначимо дужку в знаменнику за нову змінну. Далі знаходимо dx та підставимо в інтеграл
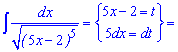
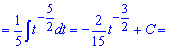
Вкінці не забуваємо повернутися до заміни, яку робили на початку.
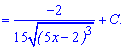
Приклад 5. Для обчислення інтегралу від дробу тригонометричних функцій слід виконати наступну заміну. Її важко помітити, однак похідна від котангенса рівна мінус одиниці розділеній на синус в квадраті, тобто знаменнику дробу. Таким чином інтеграл перетворимо до наступного
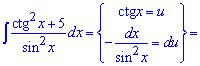
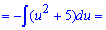
Після інтегрування підставляємо зроблену заміну.
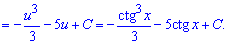
Приклад 6. Потрібно знайти інтеграл від експоненти помноженої на ірраціональну функцію від експоненти. Для спрощення вираз під коренем візьмемо за нову змінну і знайдемо решта потрібних для інтегрування величин.
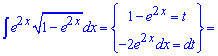
Після інтегрування повертаємося до заміни.
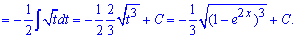
Приклад 7. На вигляд складний інтеграл має просте рішення. Все, що для Вас створює труднощі при інтегруванні позначайте за нову змінну. В цьому завданні особливість вносить функція під синусом. Її і позначимо за u, та знайдемо диференціал du
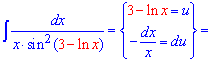
Інтеграл спроститься до табличного значення, після його знаходження виконуємо заміну змінних.
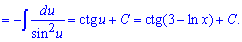
Як тільки Ви вивчите наведені схеми та методики зведення інтегралів під те чи інше правило, навчитеся бачити в прикладах табличні інтеграли та перетворення, які в кілька кроків дозволять Вам знайти інтеграл – то будь-яка контрольна робота, чи "зрізи" для Вас не будуть перешкодою в навчанні. Для цього потрібно розв'язати з десяток різних інтегралів до кожного з наведених прикладів. Всі решта після цього будуть для Вас подібними, а схема їх обчислень очевидною і зрозумілою для Вас. Якщо в навчанні зустрічаються складні інтеграли, або ж маєте сумніви у власних силах пам'ятайте – ми завжди готові надати допомогу. Як на контрольних так і на тестах, ця пропозиція актуальна не тільки для студентів стаціонарної форми навчання, а й для заочників та школярів. В 11 класі в навчанні з недавніх часів школярам також доводиться мати справу з інтегралами.
Готові розв'язки контрольної з інтегрування


