Криволінійний інтеграл I роду для кривих в полярних координатах

Продовжуємо аналізувати відповіді до прикладів на знаходження криволінійних інтегралів І роду. В цій статті піде мова про криві, які задані в полярній системі координат або можуть бути зведені до таких. Наведемо кілька завдань, які в значній мірі розкриють алгоритм знаходження криволінійних інтегралів.

Криволінійний інтеграл I роду вздовж кривих, заданих в полярних координатах

ЗАВДАННЯ 6.5 Обчислити криволінійний інтеграл:

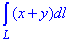
де L - правий пелюсток лемніскати

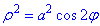
Розв'язання: Знайдемо похідну від полярного рівняння лемніскати

Рисунок лемніскати має вигляд

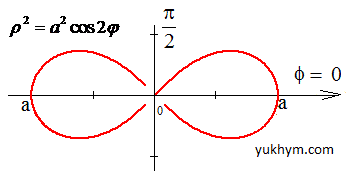
Необхідно знайти криволінійний інтеграл І роду.
Для цього обчислюємо диференціал дуги заданої кривої:

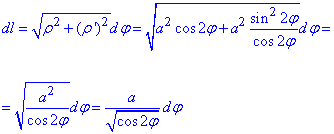
Перерахуємо підінтегральну функцію:

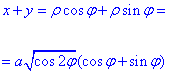
Запишемо межі інтегрування:
0≤φ≤π/4
Тут взяли чверть пелюстки, тому результат помножимо на 2 (не на 4 тому що потрібний лише правий пелюсток).
Обчислюємо криволінійний інтеграл

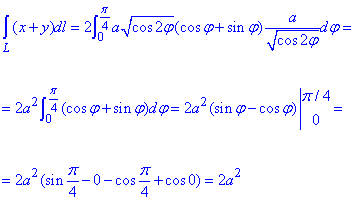
Уважно розберіть сам хід інтегрування.

ЗАВДАННЯ 6.6 Обчислити криволінійний інтеграл:

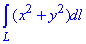
де L - коло x²+y²=ay.
Розв'язання: Зведемо рівняння до канонічного вигляду
x²+y²=ay,

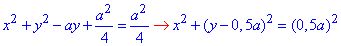
- задане коло з центром у точці O(0;0,5) і радіусом 0,5.
В декартовій площині коло має вигляд

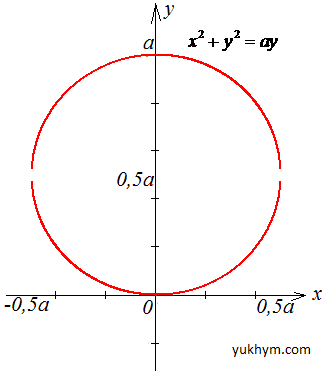
Щоб спростити обчислення криволінійного інтеграла запараметризуємо криву, щоб вона мала простий вигляд в полярній системі координат (СК).
Параметричне рівняння заданого кола отримаємо заміною змінних:

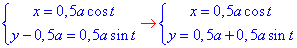
звідси

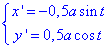
Далі обчислюємо диференціал дуги за формулою:

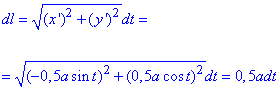
Знаходимо вигляд підінтегральної функції в полярній СК:
.
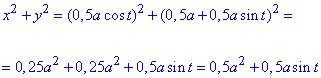Вкажемо межі інтегрування:
0≤t≤2π (параметр t пробігає по всьому колу).
Переходимо до знаходження криволінійного інтеграла І роду

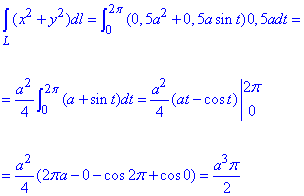
Обчислення не складні та зводяться до інтегрування сталої та синуса. Далі підставляємо межі та спрощуємо вираз.
Спробуйте самостійно знайти інтеграл для цього прикладу в декартових координатах і Ви побачите, що перехід до полярних координат зменшує час розрахунків, складність обчислень зменшується в рази.

ЗАВДАННЯ 6.7 Знайти криволінійний інтеграл:

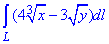
де L - дуга астроїди x=cos(3t), y=sin(3t), яка з'єднує точки A(-1;0) і B(0;1).
Розв'язання: Запишемо похідні заданих функцій:

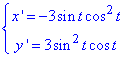
Обчислимо криволінійний інтеграл І роду вздовж наведеної нижче астроїди

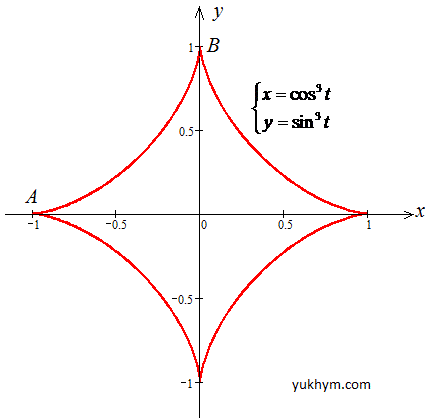
Знайдемо диференціал астроїди за формулою:
.
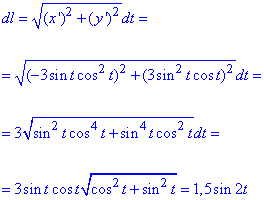Перетворимо підінтегральну функцію:
.
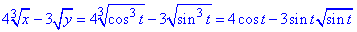Межі інтегрування належать інтервалу:
π/2≤φ≤π.
Виконуємо інтегрування

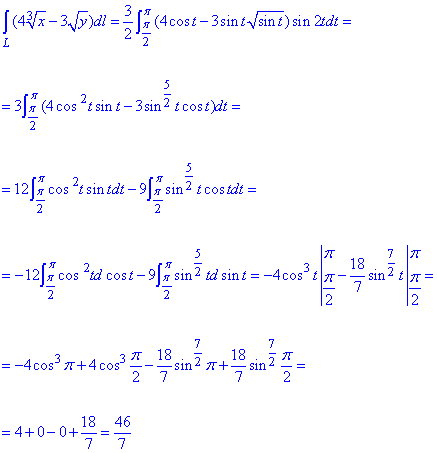
При інтегруванні довелось інтегрувати частинами. Такий спосіб досить поширений на практиці, коли маємо добуток синуса в певнім степені на косинус, або навпаки. Тут же маємо обидва випадки разом.
Проаналізуйте наскільки ефективним при інтегруванні є наведений метод.

ЗАВДАННЯ 6.8 Обчислити криволінійний інтеграл:
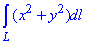, де L - коло x²+y²=9y.
Розв'язання: Перетворимо рівняння до канонічного вигляду
x²+y²=9y,

- задане коло з центром у точці O(0;4,5) і радіусом 4,5.

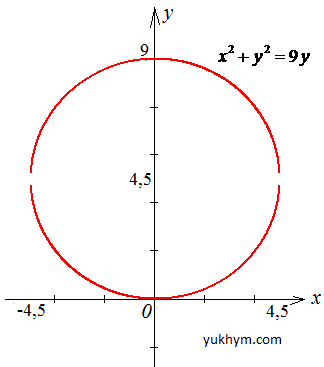
Запише параметричне рівняння заданого кола:
,
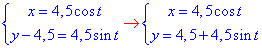звідси

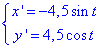
Знайдемо криволінійний інтеграл І роду вздовж дуги кола.
Для цього знайдемо диференціал дуги заданої кривої:

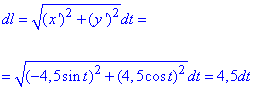
Зробимо перехід до полярної СК в підінтегральній функції:

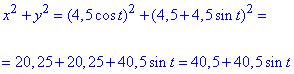
Запишемо межі інтегрування:
0≤t≤2π (параметр t пробігає по всьому колу).
Розраховуємо інтеграл

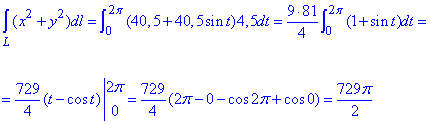
Підінтегральні функції мають простий вигляд, тому їх не важко інтегрувати.

Як можна переконатися з наведених відповідей, алгоритм обчислення криволінійного інтеграла І роду не складний.
Розрахунок диференціалу, перехід до полярної СК та саме інтегрування теж не важке, якщо не пропускати практичних та виконувати самостійно домашні завдання.
Успіху Вам у навчанні та до зустрічі на сайті!