Если кривая задана уравнением 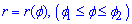 в полярной системе координат, где функция является гладкой непрерывной на промежутке
в полярной системе координат, где функция является гладкой непрерывной на промежутке 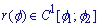 , тогда длина дуги кривой равняется определенному интегралу, рассчитанному по формуле
, тогда длина дуги кривой равняется определенному интегралу, рассчитанному по формуле
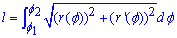
В формуле длины дуги в полярных координатах под интегралом имеем корневую функцию от суммы квадратов радиуса и его производной. Вычисления в определенной мере дружат с предыдущими публикациями, из них Вы уже знаете как вычислить длину дуг, которые заданы в декартовой системе координат и параметрически.
Примеры подобрано из программы практикума для студентов мех-мата Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький и др. "Практикум из математического анализа" (рядом стоит номер из сборника Б. П. Демидовича ).
Для изучения основных моментов схема интегрирования и формулы вычисления дуги кривой, заданной в параметрической форме повторяются из примера в пример. Часть заданий обязательно проиллюстрируем графиками кривых.
Как найти длину дуги кривой, заданной в полярных координатах?
Пример 2.132 (2446) Найти длину дуги кривой 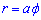 (спираль Архимеда)
(спираль Архимеда) 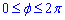 .
.
Вычисление: Найдем производную по переменной 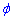 заданной функции: r'=a
заданной функции: r'=a
Пределы интегрирования известны за условием: [0;2pi].
Запишем подынтегральную функцию:
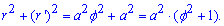
Вычислим длину дуги полярной кривой на заданном отрезке:
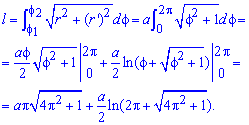
Пример 2.133 (2447) Найти длину дуги кривой 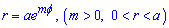 (), .
(), .
Вычисление: Найдем производную по переменной 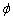 заданной функции:
заданной функции: 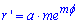
Запишем пределы интегрирования:
 при
при 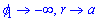 , при
, при 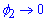 , поэтому
, поэтому 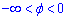
(получим несвойственный интеграл I рода, который совпадающий).
Запишем подынтегральную функцию:
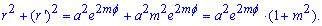
Вычислим длину дуги кривой на заданном отрезке:
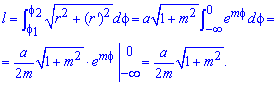
Пример 2.134 (2448) Найти длину дуги кривой 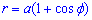 (кардиоида) (Смотри 2.107).
(кардиоида) (Смотри 2.107).
Вычисление: Найдем производную по переменной 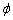 заданной функции:
заданной функции:
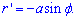
Пределы интегрирования: [0;Pi].
(найдем длину половины кривой и умножим на 2).
Запишем подынтегральную функцию:
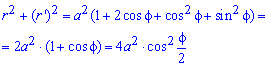
Вычислим длину дуги кривой на заданном отрезке:
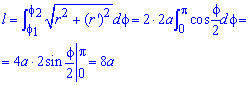
Пример 2.135 (2450) Найти длину дуги кривой 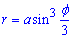 .
.
Вычисление: Найдем производную по переменной 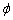 заданной функции:
заданной функции:
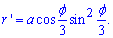
Пределы интегрирования: [0;3Pi], поскольку задана кривая замкнутая в этих пределах.
Выпишем подынтегральную функцию:
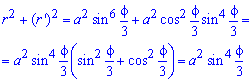
Интегрированием вычислим длину дуги кривой на заданном отрезке:
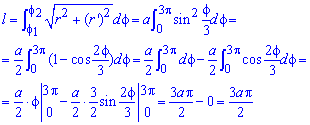
Пример 2.136 (2449) Найти длину дуги кривой 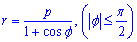 (парабола)
(парабола)
Вычисление: Найдем производную по "фи" заданной функции:

Пределы интегрирования известны из начального условия:
для параболы 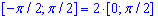
Выпишем подынтегральную функцию:
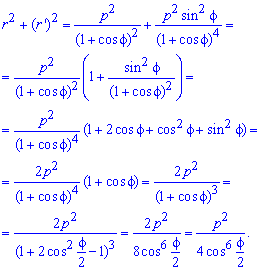
Вычислим длину дуги кривой на заданном отрезке:
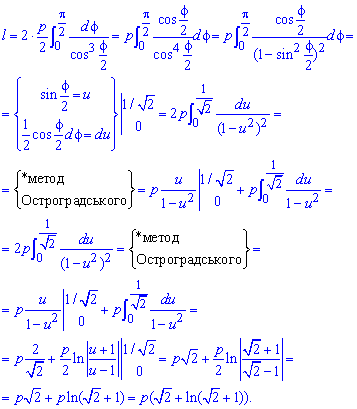
* Метод Остроградського :
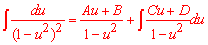
Возьмем производную от каждой части равенства (из каждого слагаемого), где 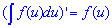
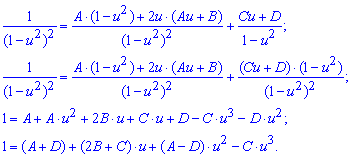
приравниваем коэффициенты при каждой переменной из двух частей равенства:
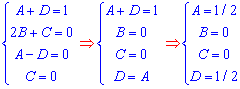
Получаем
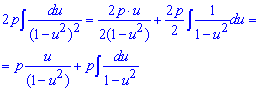 (см. выше).
(см. выше).
Пример 2.137 (2452.1) Найти длину дуги кривой 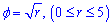 ,
,
Вычисление: Найдем производную по переменной 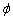 заданной функции:
заданной функции:
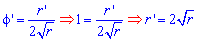
Пределы интегрирования известны: rє[0;5].
Выпишем подынтегральную функцию: 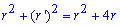
Вычислим длину дуги кривой на заданном отрезке:
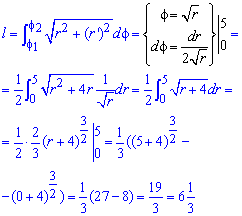
Пример 2.138 (2452) Найти длину дуги кривой 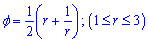 ,
,
Вычисление: Найдем производную по переменной 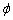 заданной функции:
заданной функции:
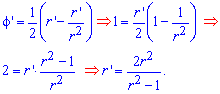
Пределы интегрирования равны: [1;3].
Выпишем подынтегральную функцию:
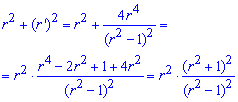
Вычислим длину дуги кривой на заданном отрезке:
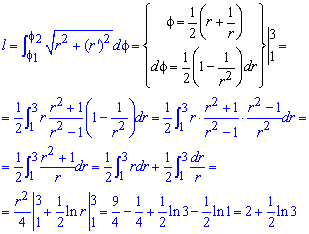
Пример 2451 Найти длину дуги кривой 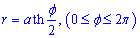 ,
,
Вычисление: Найдем производную по переменной 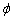 заданной функции:
заданной функции:
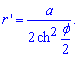
Пределы интегрирования известны за условием: [0;2pi].
Запишем подынтегральную функцию:
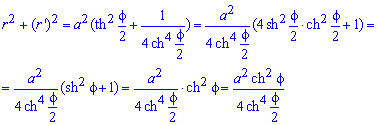
Вычислим длину дуги кривой на заданном отрезке:
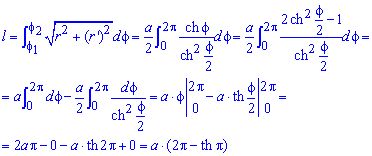
Пример 2452.2 Найти длину дуги кривой
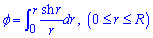
Вычисление: Найдем производную по переменной "r" заданной функции:
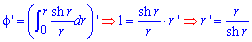
Пределы интегрирования равны: [0;R].
Запишем подынтегральную функцию:
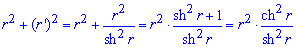
Вычислим длину дуги кривой на заданном отрезке:
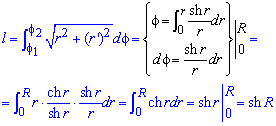
Пример 2452.3 Найти длину дуги кривой 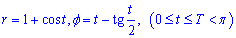
Вычисление: Найдем производную 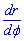 и дифференциал
и дифференциал 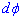 по переменной t заданных функций:
по переменной t заданных функций:
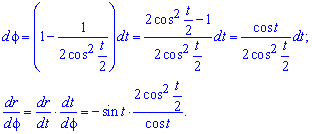
Пределы интегрирования равны: t[0;T].
Запишем подынтегральную функцию:
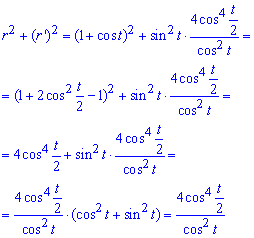
Вычислим длину дуги кривой на заданном отрезке:
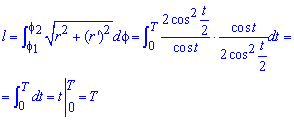
Вот и все примеры, какие мы успели Вам оформить.


