В цій категорії систематизовані приклади на різні геометричні фігури та їх складові. Окремої уваги заслуговують задачі на обчислення радіусів вписаного та описаного кіл в трикутниках. Таких завдань небагато і їх важко зібрати разом, але ми спробували на прикладі відповідей до ЗНО тестів. Пізніше доповнимо завданнями зі школи за 10-11 клас.
Завдання 26. ЗНО 2018 У прямокутному трикутнику ABC (∠C=90) відстані від середини медіани BM до катетів AC і BC дорівнюють 5 см і 6 см відповідно.
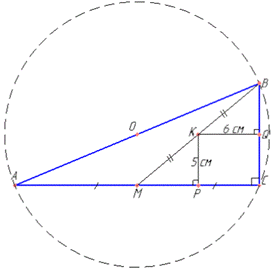
1. Визначте довжину катета AC (у см).
2. Визначте радіус (у см) кола, описаного навколо трикутника ABC.
Розв'язування: 1. Розглянемо трикутник BMC, у якого KQ=6 см - середня лінія (відстань від точки K до катета BC у ΔABC), KQ⊥BC, тому KQ||MC і MC=2•KQ=12 см.
Тоді обчислимо довжину катета AC, де AM=MC (MB - медіана ΔABC):
AC=2•MC=2•12=24 (см).
2. Розглянемо трикутник BMC, у якого KP=5 см - середня лінія (відстань від точки K до катета AC у ΔABC), KP⊥AC, тому KP||BC і BC=2•KP=10 см.
Скористаємося теоремою Піфагора для обчислення довжини гіпотенузи AB:
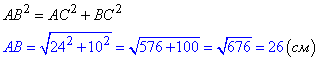
Центр кола, описаного навколо прямокутного ΔABC знаходиться на середині гіпотенузи, тому радіус R описаного кола дорівнює половині гіпотенузи
R=AB:2=26:2=13 (см).
Відповідь: 24; 13.
Приклад 30.34 У прямокутний трикутник ABC вписано коло, яке дотикається до катетів AC та BC у точках K і M відповідно.
Знайти радіус кола, описаного навколо трикутника ABC (у см), якщо AK=4,5 см, MB=6 см.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого вписане коло з центром у точці O1 і який вписаний у коло з центром у точці O2.
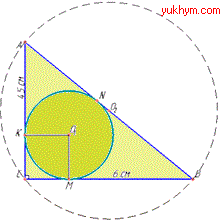
Вписане коло дотикається: до гіпотенузи AB в точці N; до катета AC в точці K; до катета BC в точці M, причому AK=4,5 см і MB=6 см (за умовою).
За властивістю трикутника і вписаного в нього кола отримаємо:
AN=AK=4,5 см, BN=BM=6 см.
Звідси отримаємо:
AB=AN+BN=4,5+6=10,5 см – гіпотенуза прямокутного ΔABC.
За властивістю кола, описаного навколо прямокутного ΔABC, отримаємо
R=AB:2=10,5:2=5,25 см – радіус описаного кола, навколо ΔABC.
Відповідь: 5,25.
Приклад 30.34а Точка дотику вписаного в прямокутний трикутник кола ділить гіпотенузу на відрізки 4 см і 6 см.
Знайти у сантиметрах радіус вписаного кола.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого вписане коло з центром у точці O.
Коло дотикається: до гіпотенузи AB в точці K, причому AK=6 см і BK=4 см (за умовою); до катета AC в точці M; до катета BC в точці N.
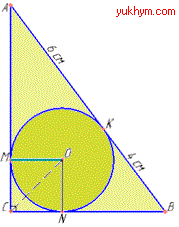
За властивістю трикутника і вписаного в нього кола отримаємо:
AM=AK=6 см, BN=BK=4 см і CM=CN (позначимо CM=CN=r) – радіус вписаного кола (це доводиться з рівності прямокутних ΔCOM (∠M=90) і ΔCON (∠N=90).
Звідси отримаємо:
AB=AK+BK=6+4=10 см – гіпотенуза, AC=AM+CM=6+r і BC=BN+CN=4+r – катети прямокутного ΔABC.
У прямокутному ΔABC за теоремою Піфагора запишемо рівність:
AC^2+BC^2=AB^2, звідси (6+r)^2+(4+r)^2=10^2, 36+12r+r^2+16+8r+r^2=100, 2r^2=20r-48=0, r^2+10r-24=0,
за теоремою Вієта, отримаємо
r1=2 і r2=-12<0,
звідси r=2 см – радіус вписаного кола в прямокутний ΔABC.
Відповідь: 2.
Приклад 30.38 У прямокутний трикутник вписано коло радіуса r.
Визначити синус меншого гострого кута трикутника, якщо довжина гіпотенузи 5r.
Розв'язування: Нехай маємо прямокутний трикутник ABC (∠C=90), у якого вписане коло з центром у точці O і радіусом r.
Коло дотикається: до гіпотенузи AB в точці K, причому AB=5r (за умовою);
до катета AC в точці M;
до катета BC в точці N.
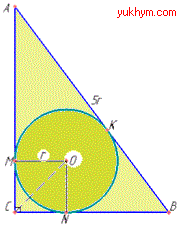
Позначимо: AK=x, тоді BK=5r-x.
За властивістю трикутника і вписаного в нього кола отримаємо:
AM=AK=x, BN=BK=5r-x, CM=CN=r (це доводиться з рівності прямокутних ΔCOM (∠M=90) і ΔCON (∠N=90).
Звідси отримаємо:
AC=AM+CM=x+r, BC=BN+CN=6r-x – катети прямокутного ΔABC.
У прямокутному ΔABC за теоремою Піфагора запишемо рівність:
AC^2+BC^2=AB^2, звідси
(x+r)^2+(6r-x)^2=(5r)^2,
x^2+2rx+r^2+36r^2-12rx+x^2=25r^2,
2x^2-10rx+12r^2=0,
x^2-5r•x+6r^2=0,
за теоремою Вієта, отримаємо
x1=2r і x2=3r.
Приймаємо x=3r, тоді отримали AC=3r+r=4r і BC=6r-3r=3r.
Обчислимо синус ∠A (меншого гострого кута прямокутного ΔABC):
sin(∠A)=BC/AB=3r/(5r)=0,6.
Відповідь: 0,6.
Надіємось, відповіді на трикутники допоможуть Вам як в шкільному навчанні, так і ЗНО підготовці, та у ВУЗах.
Поширюйте публікації в соцмережах та серед знайомих!


