Обчислити периметр та площу рівнобедреного трикутника Вам допоможе перегляд готових відповідей до завдань із ЗНО підготовки. Таким чином Ви вбиваєте двох зайців, готуєтесь до ЗНО та вчитеся розв'язувати задач на рівнобедрені трикутники.
Приклад 31.29 У рівнобедреному трикутнику центр вписаного кола ділить висоту, проведену до основи, у відношенні 12:5, а бічна сторона дорівнює 60. Знайти периметр трикутника.
Розв'язування: Нехай маємо рівнобедрений трикутник ABC, у якого AC=BC=60 - бічні сторони.
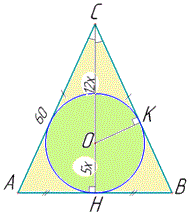
У ΔABC вписано коло з центром у точці O, причому CO:HO=12:5 (за умовою). Проведемо радіус вписаного кола OK до сторони BC, тоді OK⊥BC (за властивістю). Нехай HO=5x - радіус вписаного кола, тоді OK=HO=5x і CO=12x.
Розглянемо прямокутні ΔAHC (∠H=90) і ΔOKC (∠K=90). У них гострі кути при вершині C рівні (адже HC - висота, медіана і бісектриса).
Звідси випливає, що ΔAHC і ΔOKC подібні, а тому їх відповідні сторони пропорційні:
AC/CO=AH/OK,
звідси
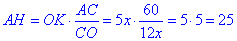
Оскільки HC - медіана, то AB=2•AH=2•25=50.
Знайдемо периметр рівнобедреного ΔABC:
PΔABC =2•AC+AB=2•60+50=170.
Відповідь: 170.
Приклад 31.30 Периметр рівнобедреного трикутника дорівнює 108 см, а основа - 30 см. Знайти (у см) площу трикутника і радіус вписаного кола.
Розв'язування: Нехай маємо рівнобедрений трикутник ABC, у якого AC=BC - бічні сторони, AB=30 см - основа і PΔABC=108 см - периметр (за умовою).
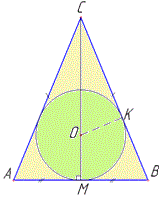
Знайдемо бічну сторону ΔABC:
PΔABC=2•AC+AB=108, звідси
AC=BC=(PΔABC–AB):2=(108-30):2=39 (см).
Проведемо висоту CM до основи AB рівнобедреного ΔABC (CM⊥AB), тоді, за властивістю, CM - медіана і бісектриса, тобто AM=BM=AB:2=30:2=15 (см).
У прямокутному ΔAMC (∠M=90) за теоремою Піфагора знайдемо катет CM - висоту ΔABC:
AM2+CM2=AC2, звідси
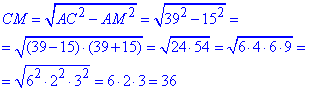
Обчислимо площу рівнобедреного трикутника ΔABC:
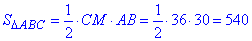(см2).
Знайдемо півпериметр ΔABC:
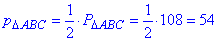(см).
Визначимо радіус вписаного кола в ΔABC за формулою:
r=S/p=540/54=10 (см).
Відповідь: 540; 10.
Приклад 31.31 Основа рівнобедреного трикутника дорівнює 12, а висота, що проведена до основи, - 8. Знайти площу трикутника і радіус кола, вписаного в цей трикутник.
Розв'язування: Нехай маємо рівнобедрений трикутник ABC, у якого AC=BC - бічні сторони, AB=12 - основа і CM=8 - висота, що проведена до основи AB, CM⊥AB (за умовою). Тоді за властивістю, CM - медіана і бісектриса, тобто
AM=BM=AB:2=12:2=6.
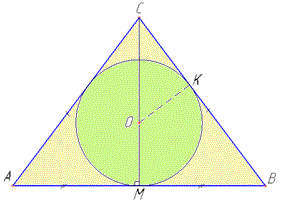
У прямокутному ΔAMC (∠M=90) за теоремою Піфагора знайдемо гіпотенузу AC - бічну сторону ΔABC:
AC^2=AM^2+CM^2, звідси
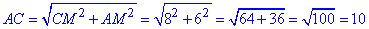
Знайдемо площу ΔABC:
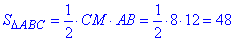
Далі півпериметр трикутника ΔABC:
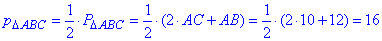
Обчислимо радіус вписаного кола в трикутнику ABC за формулою:
r=S/p=48/16=3.
Відповідь: 48; 3.
Приклад 31.35 Знайти площу рівнобедреного трикутника з точністю до 0,01 см2, якщо висота, яка проведена до бічної сторони, дорівнює 12 см, а інша висота - 9 см.
Розв'язування: Нехай маємо рівнобедрений трикутник ABC, у якого AC=BC - бічні сторони, AB - основа і CM=9 см - висота, що проведена до основи AB, CM⊥AB, AK=12 см - висота, що проведена до бічної сторони BC, AK⊥BC (за умовою).
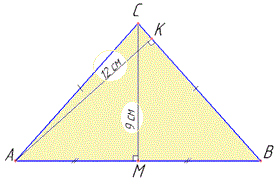
За властивістю висоти проведеної до основи рівнобедреного ΔABC: AB=2BM.
Запишемо формули для обчислення площі ΔABC:
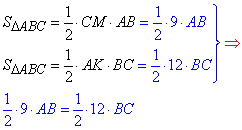
отримаємо BC=0,75*AB=0,75*2*BM=1,5BM, отже BC=1,5•BM.
У прямокутному ΔBMC (∠M=90) за теоремою Піфагора знайдемо катет BM:
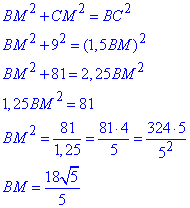
тоді AB=2•BM=36√5/5 (см).
Знайдемо площу рівнобедреного ΔABC з точністю до 0,01:
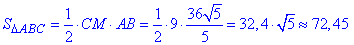
Відповідь: 72,45.
Задача 1 Центр кола, вписаного у трикутник, ділить висоту проведену до основи на відрізки 13 і 5 см. Знайти периметр трикутника.
Розв'язування: Оскільки центр кола (точка O), вписаного в трикутник ABC, лежить на висоті BM, то ΔABC – рівнобедрений.
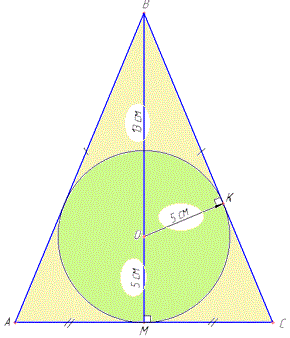
Маємо AB=BC – бічні сторони, AC – основа рівнобедреного ΔABC, BM – висота рівнобедреного трикутника ABC, проведена до основи AC (BM⊥AC). За властивістю: AM=CM, звідси AC=2CM.
За умовою задачі BM=BO+OM=13+5=18 см. OM=OK=5 см – радіус вписаного кола. За властивістю вписаного в трикутник кола OK⊥BC.
Розглянемо прямокутний трикутник OBK, у якого ∠BOK=90, OK=5 см – катет, OB=13 см – гіпотенуза. За теоремою Піфагора знайдемо катет BK:
OB^2=BK^2+OK^2, звідси
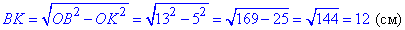
Розглянемо прямокутні трикутники OBK (∠BOK=90) і CBM (∠BMC=90).
У них ∠OBK=∠MBC (тобто гострий кут при вершині B спільний, а тому рівний). Звідси слідує, що прямокутні трикутники OBK і BCM подібні.
За властивістю подібності трикутників (сторони подібних трикутників пропорційні) маємо BK/BM=OK/CM, звідси 12/18=5/CM, CM=5•18/12=7,5 см.
За властивістю кола, вписаного в трикутник, маємо KC=CM=7,5 см.
Обчислимо довжини сторін рівнобедреного ΔABC:
AC=2CM=2•7,5=15 см;
AB=BC=BK+KC=12+7,5=19,5 см.
Обчислимо периметр трикутника ΔABC:
PΔABC=AB+BC+AC=19,5+19,5+15=54 см.
Відповідь: 54 см.
На сайті опубліковано біля 1000 завдань на різні геометричні фігури. Пояснення зрозумілі як для школяра в 10-11 класі, так і для студента. Якщо є бажання, можете доповнити будь-яку статтю якісними задачами.
Все у Ваших руках, беріть і вчіться!
- Вас може зацікавити:
- Задачі на рівнобедрений трикутник з розв'язками
- Рівнобедрений трикутник. Приклади на висоту, сторони, радіус вписаного кола
- Знаходження основи, сторін, відрізків рівнобедреного трикутника
- Обчислення висоти, основи, площі Рівнобедрений трикутника
- Рівнобедрений трикутник. Периметр і площа
