 Посібник для підготовки до ЗНО тестування з МАТЕМАТИКИ
Посібник для підготовки до ЗНО тестування з МАТЕМАТИКИ
Підручник для 9-11 класів:
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити (скачати) відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Формат: PDF
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань. Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Рік випуску: 2010 р.
Тема 29: Трикутники
Перші десять прикладів розв'язані на попередньому занятті. Всього в розділі 25 завдань на кути, бісектриси, медіани, подібність трикутників.
Далі проаналізуємо 6 завдань на властивості трикутників і в наступному уроці розберемо ще 9 прикладів.
Таким чином Ви повторите шкільний матеріал за 7, 8, 9 класи та ознайомитеся з тестовими завданнями, які можуть чекати Вас на контрольній чи ЗНО.
Задача 29.11 Два кути трикутника дорівнюють α і β, а радіус кола, описаного навколо трикутника, дорівнює R.
Визначити площу трикутника.

Обчислення: Спершу будуємо трикутник вписаний у коло та наносимо всі позначення у відповідності з умовою.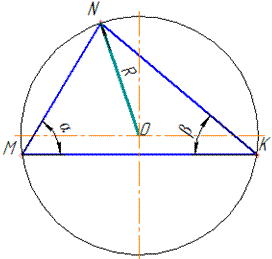
Розглянемо трикутник MNK, у якого <NMK=α і <MKN= β.
За теоремою синусів знайдемо сторони MN і MK:
MN/sin(β)=2R, звідси маємо MN=2R• sin(β). 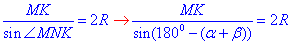
тобто, звідси маємо MN=2R• sin(α+β). де sin(180-(α +β)+ sin(α +β) за властивістю.
Обчислимо площу трикутника за двома MN і MK сторонами і кутом між ними <NMK:
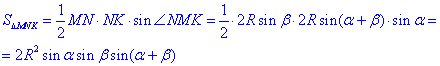
Відповідь: Д.
Задача 29.12 Дві сторони трикутника дорівнюють 48 см і 28 см. Указати всі можливі значення периметра трикутника.
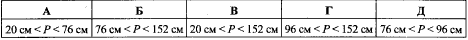
Обчислення: Нехай маємо трикутник ABC і AB=48 см, BC=28 см.
За властивістю трикутника маємо:
сума двох сторін довільного трикутника завжди більша за третю;
третя сторона довільного трикутника більша за різницю двох інших сторін цього ж трикутника.
Отже, AB-BC<AC<AB+BC,
тоді за властивістю нерівності запишемо:
AB_BC+AB+BC<AB+BC+AC<AB+BC+AB+BC,
2AB<PABC<2(AB+BC),
де PABC=AB+BC+AC - периметр трикутника ABC.
Підставивши задані значення сторін трикутника, отримаємо
2•28<PABC<2(48+28),
або
96 см< PABC см.
Відповідь: 96 см< PABC см – Г.
Задача 29.13 O – точка перетину бісектрис AK і BL трикутника ABC.
Знайти <AOB, якщо <C=50.

Обчислення: Побудуємо трикутник за умовою завдання
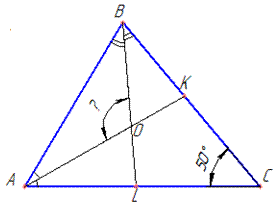
За теоремою про суму кутів трикутника маємо:
<A+<B=180-<C=180-50=130, тоді (<A+<B)/2=65.
Оскільки AK і BL – бісектриси трикутника ABC, то
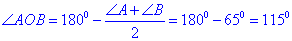
Відповідь: 115 – Б.
Задача 29.14 Градусні міри зовнішніх кутів трикутника ABC при вершинах A, B і C відносяться як 3:4:5.
Як відносяться градусні міри внутрішніх кутів трикутника при вершинах A, B і C.

Обчислення: Нехай градусна міра однієї частинки кожного зовнішнього кута трикутника ABC дорівнює x.(див. рисунок)
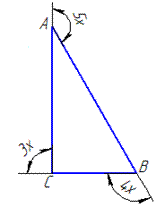
Тоді градусні міри трьох зовнішніх кутів трикутника дорівнюють (за умовою):
3x, 4x і 5x.
За теоремою про суму зовнішніх кутів трикутника маємо:
3x+4x+5x=360, звідси
12x=360,
x=360/12=30.
Градусні міри зовнішніх кутів трикутника ABC при вершинах A, B і C:
3•30=90,
4•30=120 і
5•30=150.
Оскільки внутрішній кут трикутника є суміжним із відповідним йому зовнішнім кутом, то за теоремою про суму суміжних кутів маємо:
180-90=90,
180-120=60 і
180-150=30 - внутрішні кути ΔABC.
Отож, запишемо відношення градусних мір внутрішніх кутів при вершинах A, B і C:
90:60:30, або 3:2:1.
Відповідь: 3:2:1– В.
Задача 29.15 Кути трикутника відносяться як 1:2:3.
Знайти відношення протилежних їм сторін.
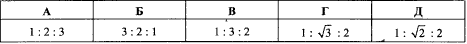
Обчислення: Завданн за алгоритмом обчислень подібне до попереднього.
Спершу побудуємо трикутник до задачі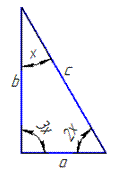 Нехай градусна міра однієї частинки кожного кута дорівнює x.
Нехай градусна міра однієї частинки кожного кута дорівнює x.
Тоді градусні міри трьох кутів трикутника дорівнюють (за умовою):
x, 2x і 3x.
За теоремою про суму кутів трикутника маємо:
x+2x+3x=180.
Розв'яжемо отримане рівняння і знайдемо x:
6x=180, x=180/6=30.
Отримали наступні градусні міри кутів:
α=30, β=60 і hamma=90.
За теоремою синусів запишемо рівність:
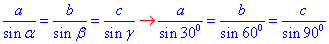
звідси 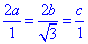
з цього слідує:
a=1•a, 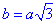 , c=2a.
, c=2a.
Тому маємо відношення сторін:
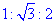
Відповідь: – Г.
Задача 29.16 Сторони трикутника дорівнюють 7 см, 8 см і 10 см.
Знайти косинус найбільшого кута цього трикутника.

Обчислення: Проти більшої сторони лежить більший кут, і навпаки, проти меншої сторони лежить менший кут.
Це Ви повинні вивчити і знати, як одну з важливих властивостей трикутника
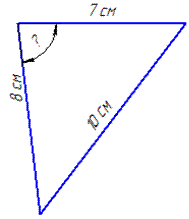
Тому косинус кута будемо шукати напроти сторони, що дорівнює 10 см за теоремою косинусів:
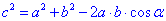
Тут c=10 см, a=7 см і b=8см.
Отже,
10^2=7^2+8^2-2•8•7•cos(α),
100=49+64-112•cos(α),
112•cos(α)=13.
Відповідь: cos(α)=13/112 - Г.
Сподіваємося Вам сподобалися пояснення до прикладів.
Далі наведемо готові відповіді до 9 прикладів на трикутники, які допоможуть в підготовці до ЗНО з математики.


