Розглянемо готові задачі на кулю та одну або декілька дотичних площин. Такого плану завдання Вас чекають як в курсі шкільної геометрії, так і при проходженні ЗНО тестування для вступу у ВУЗи.
Умови задач дещо перекликаються між собою, тому якщо зрозумієте як обчислювати наведені завдання, то подібні для Вас не будуть складними.
Тут Вам необхідно добре знати теорему Піфагора, властивості дотичної площини та вміння добре накреслити малюнок або уявити, що матимемо в перерізі.
Задача 40.2 Діаметр кулі дорівнює 6 см. Точка A лежить на дотичній площині на відстані 4 см від точки дотику.
Знайти відстань від точки A до поверхні кулі.
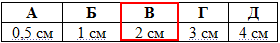
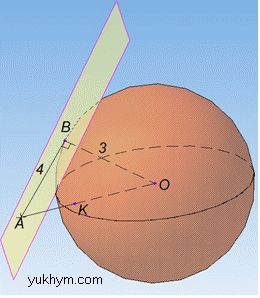
Розв'язання: Маємо кулю з діаметром D=6 см.
Тоді радіус кулі:
R=D/2=3см.
Маємо дотичну площину до кулі, яка (за властивістю) в точці дотику (точка B) перпендикулярна до радіуса BO.
Це означає, що радіус BO перпендикулярний до кожної прямої, що лежить в заданій дотичній площині, звідси BO⊥AB, де відрізок AB=4 см – відстань від точки A до точки дотику B. Це важливо знати і використовувати в доведенні багатьох тверджень.
Проведемо відрізок AO – відстань від точки A до центра кулі.
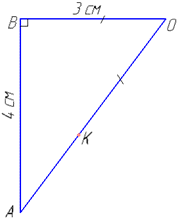
Цей відрізок перетинає кулю в точці K, тоді KO=BO=R=3 см – радіус кулі, а AK – відстань від точки A до поверхні кулі.
Із прямокутного трикутника ABO (∠ABO=90), в якому BO=3 см і AB=4 см – катети, за теоремою Піфагора знайдемо гіпотенузу AO:
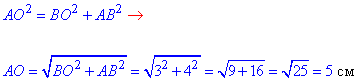
Отже, AO=5 см, тоді AK=AO-KO=5-3=2 см – відстань від точки A до поверхні кулі.
Відповідь: 2 см – В.
Задача 40.13 Вершини трикутника лежать на сфері радіуса 13 см.
Знайти відстань від центра сфери до площини трикутника, якщо сторони трикутника дорівнюють 6 см, 8 см і 10 см.
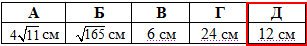
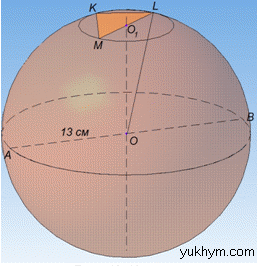
Маємо сферу з центром O і радіусом R=13 см.
Розв'язання:Маємо трикутник KLM зі сторонами KL=8 см, KM=6 см і LM=10 см, вершини якого лежать на сфері.
За властивістю: через три точки можна провести площину.
Ця площина перетинає сферу по колу з центром O1, яке є описаним навколо ΔKLM.
Відрізок OO1 – відстань від центра сфери до площини ΔKLM, тому OO1⊥LM, зокрема OO1⊥LO1.
Оскільки вершини ΔKLM лежать на сфері, то MO=KO=LO=R=13 см – радіус сфери.
Неважко переконатися, що LM2=KM2+KL2 (102=62+82), звідси слідує, що ΔKLM – прямокутний (∠MKL=90) з катетами KL=8 см, KM=6 см і гіпотенузою LM=10 см.
За властивістю, якщо навколо прямокутного ΔKLM описане коло, то його радіус дорівнює половині гіпотенузи:
LO1=LM/2=10/2=5см.
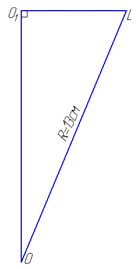
Розглянемо прямокутний трикутник OO1L (∠OO1L=90), в якому LO1=5 см – катет, LO=R=13 см – гіпотенуза за теоремою Піфагора знайдемо катет OO1:
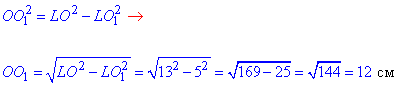
Отже, OO1=12 см – відстань від центра сфери до площини ΔKLM.
Відповідь: 12 см – Д.
Задача 40.14 Вершини прямокутника лежать на сфері радіуса 10 см.
Знайти відстань від центра сфери до площини прямокутника, якщо його діагональ дорівнює 16 см.
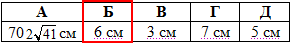
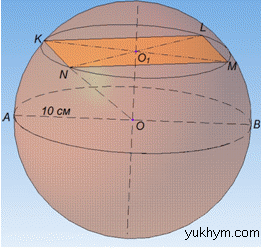
Розв'язання: Маємо сферу з центром O і радіусом R=10 см.
Маємо прямокутник KLMN з діагоналлю LN=16 см, вершини якого лежать на сфері.
Діагональ LN розбиває прямокутник KLMN на два рівних прямокутних трикутники KLN і LMN.
За властивістю: через три точки можна провести площину.
Ця площина перетинає сферу по колу з центром O1, яке є описаним навколо прямокутного ΔKLN.
Відрізок OO1 – відстань від центра сфери до площини прямокутника KLMN, або до площини ΔKLN, тому OO1⊥LN, зокрема OO1⊥NO1.
Оскільки вершини прямокутника KLMN лежать на сфері, то MO=KO=LO=NO=R=10 см – радіус сфери.
У прямокутника, що вписаний в коло, половина діагоналі є радіусом описаного навколо нього кола (за властивістю), тобто NO1=LN/2=16/2=8 см.
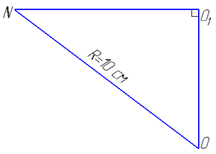
Розглянемо прямокутний трикутник OO1N (∠OO1N=90), в якому NO1=8 см – катет, NO=R=10 см – гіпотенуза.
За теоремою Піфагора знайдемо катет OO1:
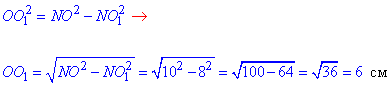
Отже, OO1=6 см – відстань від центра сфери до площини прямокутника KLMN.
Відповідь: 6 см – Б.
Задача 40.15 Через точку, що лежить на поверхні сфери, проведено дві взаємно- перпендикулярні площини, які перетинають сферу по колах з радіусами r1 і r2.
Визначити площу поверхні сфери.
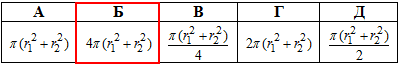
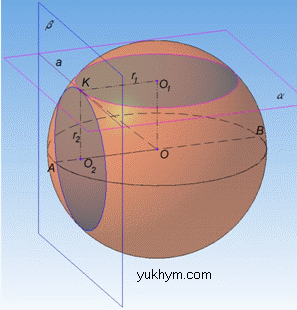
Розв'язання: Площу поверхні сфери обчислюють за формулою:
S=4πR2, де R– радіус сфери.
Маємо сферу з центром O, який перетнутий двома взаємно- перпендикулярними площинами alpha і beta.
Ці площини перетинають сферу по колах з центрами O1, O2 і радіусами r1, r2 відповідно.
За умовою задачі, площини alpha і beta проведені через точку (нехай K), що лежить на поверхні сфери, тому кола дотикаються одне до одного в цій точці, отже за властивістю перпендикулярності площин: KO1⊥KO2, де KO1=r1, KO2=r2.
Проведемо відрізки OO1 і OO2 – відстані від центра сфери до центрів відповідних кіл, тому KO1⊥OO1 і KO2⊥OO2.
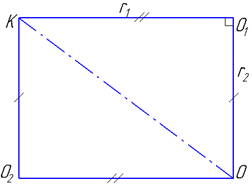
Звідси слідує, що чотирикутник OO1KO2 – прямокутник зі сторонами KO1=OO2=r1, KO2=OO1=r2 і діагоналлю KO=R (тобто радіуса сфери).
Із прямокутного ΔOO1K (∠OO1K=90) за теоремою Піфагора встановлюємо діагональ:
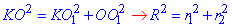
Площа поверхні сфери рівна:
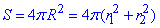
Відповідь: 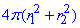 – Б.
– Б.
Задача 40.16 Через точку, що не лежить на сфері, проведено дві площини, які дотикаються до сфери. Знайти відстань від центра сфери до лінії перетину площин, якщо кут між площинами дорівнює 60, а площа поверхні сфери – 32π см2.
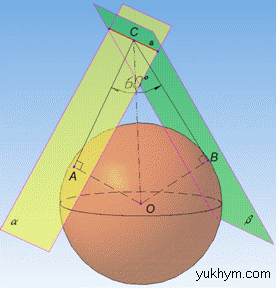
Розв'язання: Маємо сферу з центром O і площею поверхні: S=32π см2.
Площу поверхні сфери обчислюють за формулою:
S=4πR2. Звідси отримаємо, 32π=4πR2, 8•4π=4π•R2 тобто R2=8, або R=2√2 см – радіус сфери.
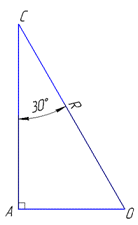
За умовою задачі, через точку (нехай C) проведені площини α і β, які утворюють між собою кут 60 і дотикаються до сфери у точках A і B відповідно.
Проведемо радіуси сфери AO=R=2√2 см і BO=R=2√2 см, які перпендикулярні до дотичних площин α і β відповідно (за властивістю).
До лінії перетину площин, а саме до точки C, проведемо перпендикуляри AC і BC, які належать площинам α і β відповідно, оскільки точки A, B і C належать їм.
Звідси слідує, що ∠ACB=60 – кут між площинами α і β.
З того, що α і β – дотичні площини до сфери, то AO⊥AC і BO⊥BC.
Проведемо відрізок CO – відстань від центра сфери до лінії перетину площин. Тоді отримаємо рівні прямокутні ΔAOC (∠OAC=90) і  (∠OBC=90) за гіпотенузою CO (спільна) і катетами AO=BO=R=2√2 см (як радіуси сфери).
(∠OBC=90) за гіпотенузою CO (спільна) і катетами AO=BO=R=2√2 см (як радіуси сфери).
Тому 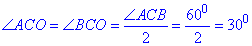
Розглянемо прямокутний ΔAOC (∠OAC=90), у якого AO=2√2 см – протилежний катет до кута ∠ACO=30.
За означенням синуса гострого кута прямокутного трикутника знайдемо гіпотенузу CO:
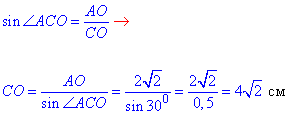
Отже, CO=4√2 см – відстань від центра сфери О до лінії перетину площин α і β.
Відповідь: 4√2 см – А.
Задача 40.25 Дві площини, які перетинаються під кутом 60 градусів, дотикаються до сфери. Установити відповідність між площею поверхні сфери (1–4) та відстанню від її центра до лінії перетину цих площин (А–Д).
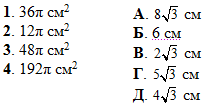
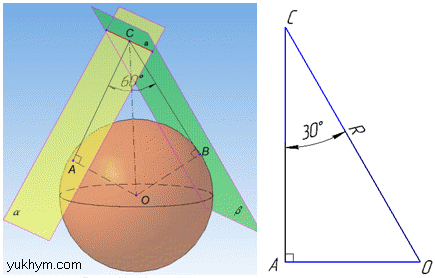
Розв'язання:
Розв'язок цієї задачі і задачі 40.16 можна звести до наступної залежності:
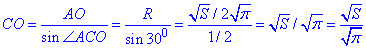
де S=4πR^2 – площа поверхні сфери радіуса R, звідки
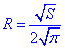
Обчислимо відстань CO від центра сфери O до лінії перетину площин α і β:
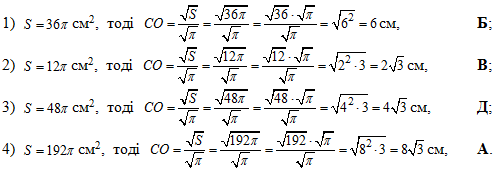
Більше задач на площу поверхню кулі (сфери), знаходження об'єму, радіуса міститься в сусідніх статтях.


