Задачі на площу трапеції розв'язують в шкільному курсі планіметрії. Розрахунки не надто складні при вивченні цієї теми, однак з плином часу забувається і теоретичний матеріал і формули для обчислення площі трапеції. З даного матеріалу Ви навчитеся знаходити площу трапеції та ознайомитеся з поширеними для обчислень формулами.
Формули площі трапеції
1. Площа трапеції рівна добутку півсуми основ на висоту:
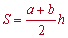
Середня лінія трапеції рівна півсумі основ, тому попередню формулу площі можна записати у вигляді
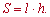
Нижче на рисунку наведено відповідні формули та позначення
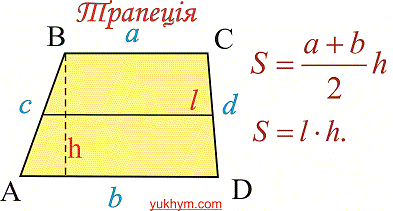
2. Якщо задано діагоналі трапеції та кут між ними (див. рис.),
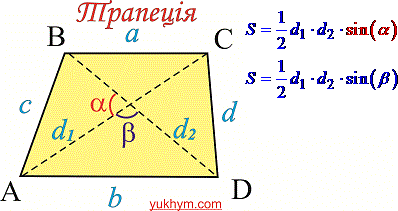
то площу трапеції знаходять через половину добутку діагоналей трапеції на синус кута між ними.
Варто зазначити, що неважливо чи тупий чи гострий кут підставляємо у формулу.
Значення площі від цього не поміняється.
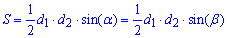
Дана формула, як і попередня, достатньо проста в обчисленнях.
Наступна формула вимагає більшої кількості розрахунків.
3. Бувають складні приклади на трапецію, коли задано усі чотири її сторони. В таких випадках використовують першу формулу площі трапеції
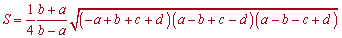
або другу
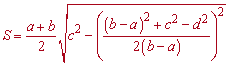
При застосуванні формули слід пам'ятати, що між сторонами повинні виконуватися умови b>a і c>d.
4. Якщо в завданні відомо, що трапеція рівнобічна (бічні сторони рівні) то для того, щоб знайти площу трапеції крім вище наведених формул використовують наступні:
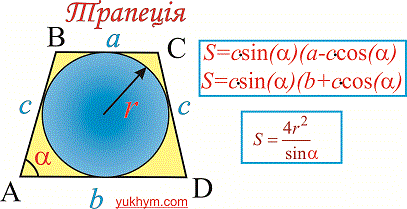
- якщо задано основу, бічну сторону та кут між ними
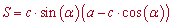
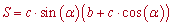
- якщо відомий радіус вписаного кола та кут при основі
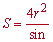
Тут r – радіус вписанного кола, alpha – кут при основі, c – бічна сторона рівнобічної трапеції.
Якщо радіуса вписаного кола та потрібного кута не задано в умові прикладу – користуйтеся вище наведеними формулами площі трапеції.
Тепер Ви знаєте як знайти площу трапеції, використовуйте наведені формули на практиці та не майте проблем у навчанні.
Далі розглянемо готові відповіді до прикладів на трапеції та покажемо, як застосовувати формули площі на практиці.


