Встановлення асиметрії та ексцесу дозволяє встановити симетричність розподілу випадкової величини X відносно M(X)=1. Для цього знаходять третій центральний момент, що характеризує асиметрію закону розподілу випадкової величини. Якщо він рівний нулю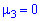 
, то випадкова величина X симетрично розподілена відносно математичного сподівання M(X). Оскільки момент 
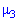має розмірність випадкової величини в кубі, то вводять безрозмірну величину — коефіцієнт асиметрії:
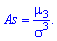
Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності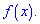 
Ексцес обчислюється за формулою
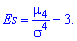
Число 3 віднімається для порівняння відхилення від центрального закону розподілу (нормального закону), для якого справджується рівність:
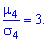
Отже, ексцес рівний нулю Es=0 для нормального закону розподілу. Якщо ексцес додатній Es>0 то на графіку функція розподілу має гостру вершину і для від'ємних значень Es<0 більш пологу. В такий спосіб можна встановити відхилення заданого закону від нормального. Для наочності при різних значеннях асиметрії і ексцесу Es<0 графіки щільності ймовірностей f(x) зображені на рисунках нижче
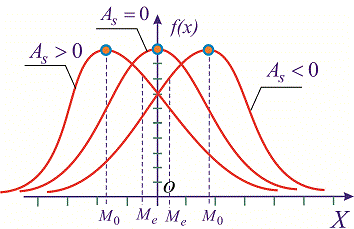
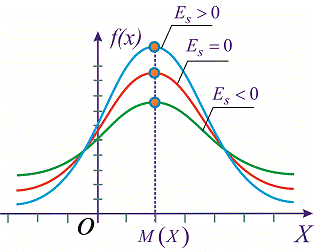
Наведу Вам один з поширених прикладів.
Приклад 1. Задано щільність імовірностей:
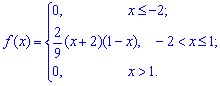
Обчислити асиметрію та ексцес As, Es.
Розв'язання. Обчислюємо математичне сподівання випадкової величини
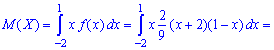
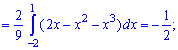
після цього - третій момент інерції
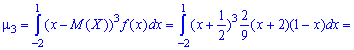
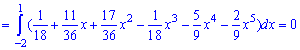
Оскільки момент нульовий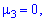 
то і асиметрія рівна нулю As=0 .Отже, можливі значення випадкової величини X симетрично розподілені відносно одиниці M(x)=1. Для обчислення ексцесу Es необхідно знайти четвертий момент 
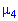та середнє квадратичне відхилення 
.
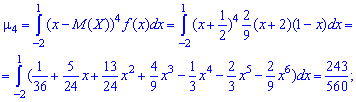
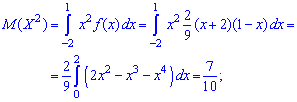
За допомогою знайдених значень обчислюємо дисперсію
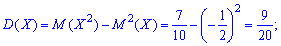
після неї середнє квадратичне відхилення
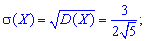
Тепер можемо знайти ексцес
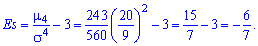
Від'ємний знак ексцесу вказує на пологість функції розподілу. Сам графік функції із знайденими величинами наведено нижче.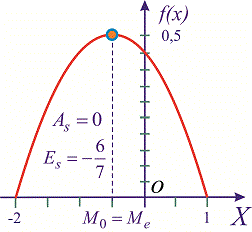
Добре розберіть наведений приклад, всі інші подібні. Знайти асиметрію та ексцес досить легко числити тим, хто добре вміє інтегрувати та не поспішає при обчисленнях.
