Знайти моду, медіану, дисперсію та інші характеристики вчать в курсі ймовірності для аналізу статистичного розподілу вибірки. Якщо мати заготовлені формули або методичку, то саме по собі обчислення числових характеристик статистичних вибірок не є складним. Однак на контрольних чи індивідуальних завданнях, а ще для заочників все завжди виглядає складнішим ніж є насправді. Нижче наведені розв'язки, які багато речей з ймовірності зроблять для Вас простими та зрозумілими. Головне не спішіть і в подібних завданнях поступайте по аналогії.
Практикум з ТІМС
Обчислення моди, медіани, дисперсії, середнього квадратичного відхилення, коефієнта асиметрії та ексцесу
Завдання 1. Побудувати статистичний розподіл вибірки, записати емпіричну функцію розподілу та обчислити такі числові характеристики:
- вибіркове середнє;
- вибіркову дисперсію;
- підправлену дисперсію;
- вибіркове середнє квадратичне відхилення;
- підправлене середнє квадратичне відхилення;
- розмах вибірки;
- медіану;
- моду;
- квантильне відхилення;
- коефіцієнт варіації;
- коефіцієнт асиметрії ;
- ексцес для вибірки:
Вибірка задана наступними значеннями
4, 9, 7, 4, 7, 5, 6, 3, 4, 5, 7, 2, 3, 8, 5, 6, 7, 4, 3, 4.
Розв'язання: Записуємо вибірку у вигляді варіаційного ряду (у порядку зростання):
2; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 7; 7; 7; 7; 8; 9.
Запишемо статистичний розподіл вибірки у вигляді дискретного статистичного розподілу частот:
![]()
Значення емпіричної функції розподілу визначаємо за формулою
![]()
де nx кількість елементів вибірки, що менші за х. Використовуючи таблицю, а також враховуючи, що обсяг вибірки n=1+3+5+3+2+4+1+1=20, запишемо емпіричну функцію розподілу:
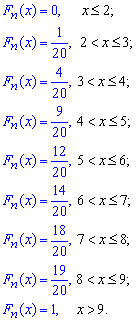
Далі обчислимо числові характеристики статистичного розподілу вибірки.
1. Вибіркове середнє обчислюємо за формулою
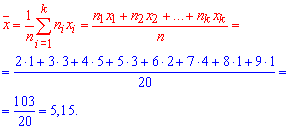
2. Вибіркову дисперсію обчислюємо за формулою
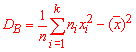
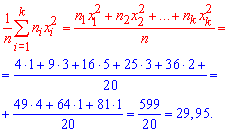
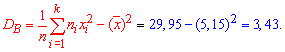
3. Підправлену дисперсію встановлюємо за формулою
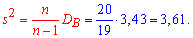
4. Вибіркове середнє квадратичне відхилення обчислюємо за формулою
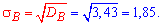
5. Підправлене середнє квадратичне відхилення знаходимо за формулою
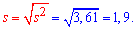
6. Розмах вибірки обчислюємо як різницю між найбільшим і найменшим значеннями її варіант, тобто:
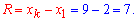
7. Медіану визначають за формулами:
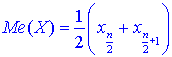 якщо число n – парне;
якщо число n – парне;
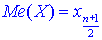 якщо число n – непарне.
якщо число n – непарне.
Тут беремо індекси в x[i] згідно з нумерацією варіант у варіаційному ряді.
У нашому випадку п=20, тому
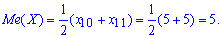
8. Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
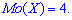
9. Квантильне відхилення знайдемо за формулою
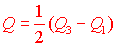
половини різниці 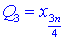 – третього та
– третього та 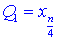 – першого квантилів.
– першого квантилів.
Самі ж квантилі отримуємо штучним розбиттям варіаційного ряду на 4 однакові частини. У нашому випадку
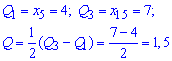
10. Коефіцієнт варіації обчислюємо за формулою
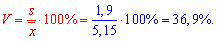
11. Коефіцієнт асиметрії знаходимо за формулою
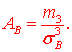
Тут m3 центральний емпіричний момент 3-го порядку,
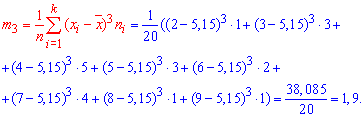
Звідси коефіцієнт асиметрії рівний 0,3
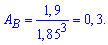
12. Ексцесом EB статистичного розподілу вибірки називається число, яке знаходять за формулою:
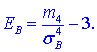
В чисельнику маємо m4 центральний емпіричний момент 4-го порядку,
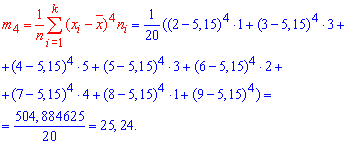
Момент та середня квадратичне відхилення підставляємо у формулу та визначаємо ексцес
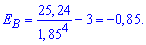
ПРАКТИКУМ з теорії ймовірностей і математичної статистики
Завдання 4.1 За даними вибірки знайти моду та медіану.
xi | 1 | 3 | 4 | 5 | 8 | 9 |
ni | 30 | 19 | 10 | 16 | 15 | 10 |
Розв'язування: Мода – це варіанта, яка у варіаційному ряді трапляється найчастіше, тобто
M0(X)=1,
(адже при найбільшій частоті n=30 маємо x30=1).
Формули медіани для дискретного закону розподілу мають вигляд:
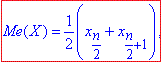 якщо число n= ∑ni – парне,
якщо число n= ∑ni – парне,
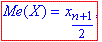 якщо число n – непарне,
якщо число n – непарне,
тут беремо індекси в xi згідно з нумерацією варіант у варіаційному ряді, у нашому випадку n=∑ni=100, (при n=50 маємо x50=4 і при n=51 маємо x51=4), тому
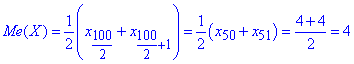
Відповідь: M0(X)=1, Me(X)=4.
Завдання 4.2 За даними вибірки знайти середнє вибіркове 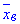 .
.
xi | 1 | 3 | 4 | 5 | 8 | 9 |
ni | 30 | 19 | 10 | 16 | 15 | 10 |
Розв'язування: Вибіркове середнє x знаходимо за формулою
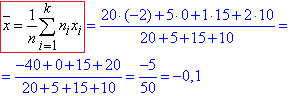
Відповідь: x=-0,1.
З того, як все доступно і зрозуміло на практиці виглядає робимо висновок, що знайти моду, медіану та дисперсію повинен вміти кожен, хто вивчає ймовірність.


