Задачі на знаходження координат точок, канонічних рівнянь кіл, сфер, обчислення відстані на площині та в просторі Ви повинні навчитися швидко та правильно розв'язувати, щоб успішно скласти ЗНО тести, вступні іспити та не мати проблем з навчанням у ВУЗах. Далі наведені 32 готові відповіді до ЗНО тестів на тему 41. Координати.
Приклад 41.1 Точки A(2;-4;-8) і B(10;-20;6) симетричні відносно точки C. Знайти координати точки C.
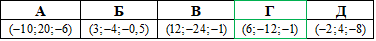
Розв'язування: Щоб Ви могли з легкістю розуміти всі текстові пояснення до формул, нами виконані допоміжні рисунки до завдань.
Це допоможе доказати (нехай і візуальна) ряд теорем та властивостей, які Ви повинні знати з теоретичного матеріалу. Плюс це Вам багато допоможе в навчанні і читанні формул.
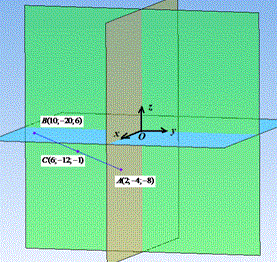
Якщо точки A(2;-4;-8) і B(10;-20;6) симетричні відносно точки C, то це означає, що точка C є серединою відрізку AB.
За формулою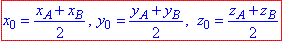 
знайдемо координати середини відрізка AB.
(Якщо відрізок знаходиться у площині xOy, то третя координата z відсутня).
Виконуємо обчислення
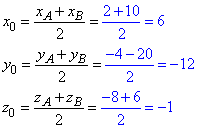
C(6;-12;-1) - координати шуканої точки C.
Відповідь: (6;-12;-1) – Г.
Приклад 41.2 На координатній площині xOy зображене коло, центр якого збігається з початком координат (див рисунок). Точки K(8;6) і M(x;y) належать колу. Визначте координати точки M.
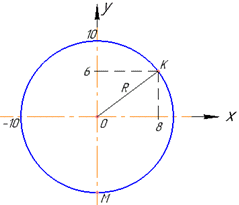
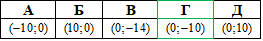
Розв'язування: Знайдемо радіус R кола як відстань між точками O(0;0) (початок координат, центр кола) і K(8;6) (точкою на колі).
- відстань між точками O і K (довжина OK відрізка ) на площині xOy.
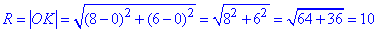
Відрізки OK і OM рівні як радіуси кола (OK=OM=R=10), тому точка M має координати (0;-10), оскільки належить колу і від’ємній півосі ординат Oy, тобто M(0;-10).
Відповідь: (0;-10) – Г.
Приклад 41.3 Дано трикутник ABC, вершини якого мають координати A(-2;6), B(-2;2) і C(4;-2). Знайти довжину медіани BM.
А | Б | В | Г | Д |
2 | 3 | 4 | 5 | 6 |
Розв'язування: Медіана трикутника - відрізок, який виходить з вершини трикутника і ділить протилежну сторону навпіл, тобто AM=MC (див.рис.).
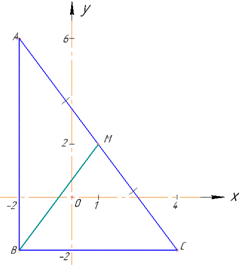
Знайдемо координати середини відрізка AC, тобто координати точки M:
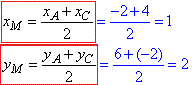
звідси M(1;2).
Знайдемо довжину відрізка (медіани) BM - відстань між точками B і M за формулою:
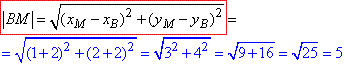
Відповідь: 5 – Г.
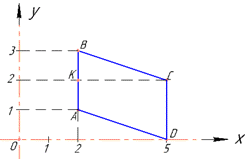
Приклад 41.4 Обчислити площу чотирикутника ABCD (див. рисунок), сторони AB і CD якого паралельні осі Oy.
А | Б | В | Г | Д |
10 | 5 | 3 | 6 | 7 |
Розв'язування: Оскільки AB||Oy і CD||Oy (звідси AB||CD), то заданий чотирикутник ABCD – трапеція з основами
|AB|=|yB-yA|=|3-1|=2 і |CD|=|yD-yC|=|0-2|=2.
Проведемо відрізок CK||Ox, звідси CK⊥AB, тому відрізок CK– висота трапеції ABCD.
За формулою площі трапеції через добуток середньої лінії на висоту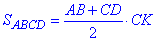
отримаємо
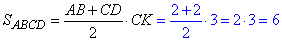
ІІ – спосіб.
Можна довести, що заданий чотирикутник ABCD – паралелограм. Тому за формулою площі паралелограма SABCD=AB•CK отримаємо
SABCD=AB•CK=2•3=6.
Відповідь: 6 – Г.
Приклад 41.5 Знайти координати точки, яка симетрична точці A(1;2;3) відносно площини xOy.
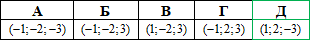
Розв'язування: Якщо точка B(x;y;z) симетрична точці A(1;2;3) відносно площини xOy, то координати абсциси x і ординати y обох точок співпадають, а координата аплікати z змінює свій знак на протилежний, отже точка B(1;2;-3) симетрична точці A(1;2;3) відносно площини xOy. Щоб мати уявлення як це виглядає в просторі до цього та наступних завдань побудовані зрізи 3d рисунків. З них Вам стане ясно чому так є, та загалом хід викладених міркувань.
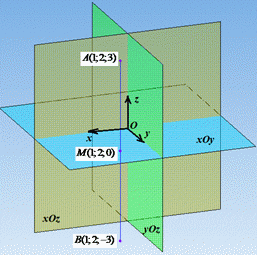
Точка M(1;2;0) є серединою відрізка AB і належить площині xOy (точки A і B симетричні відносно точки M).
Відповідь: (1;2;-3) – Д.
Приклад 41.6 Знайти координати точки, яка симетрична точці A(10;20;30) відносно осі аплікат.
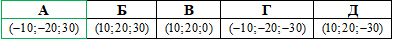
Розв'язування: Якщо точка B(x;y;z) симетрична точці A(10;20;30) відносно осі аплікат (осі Oz), то координати аплікати z обох точок співпадають, а координати абсциси x і ординати y змінюють свій знак на протилежний, отже точка B(-10;-20;30) симетрична точці A(10;20;30) відносно осі аплікат (осі Oz).
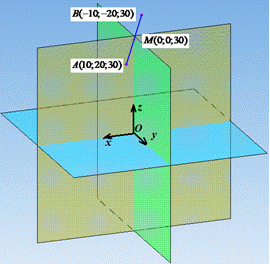
Точка M(0;0;30) є серединою відрізка AB і належить осі Oz (точки A і B симетричні відносно точки M).
Відповідь: (-10;-20;30) – А.
Приклад 41.7 При паралельному перенесенні точка A(1;2;6) переходить у точку A1(6;7;0). Вказати координати точки, у яку при цьому переходить точка B(7;9;1).
Розв'язування: Знайдемо координати вектора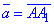 
, при якому здійснюється паралельне перенесення з точки A(1;2;6) в точку A1(6;7;0):
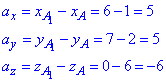
Напрямний вектор рівний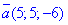 
. Наведемо просторовий рисунок до завдання
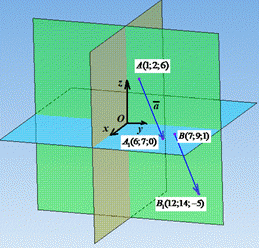Знайдемо координати точки B1(x;y;z), у яку переходить точка B(7;9;1) при паралельному перенесенні на вектор 
:
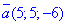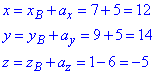
Записуємо у вигляді B1(12;14;-5).
Відповідь: (12;14;-5) – В.
Приклад 41.8 Знайти відстань від точки M(5;4;12) до осі ординат.
А | Б | В | Г | Д |
5 | 4 | 12 | 13 | 21 |
Розв'язування: Відстань від точки до прямої (в просторі) – це перпендикуляр опущений з точки на пряму.
Проведемо перпендикуляр MA до площини xOy і поставимо точку A(5;4;0), проведемо перпендикуляр AB до площини yOz (до осі Oy) і поставимо точку B(0;4;0).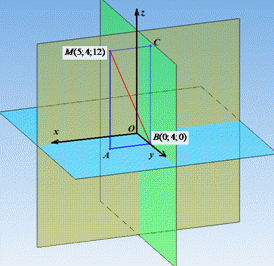 
Проведемо похилу MB до площини xOy, тоді AB її проекція на цю площину. Оскільки AB⊥Oy, то за теоремою про три перпендикуляри BM⊥Oy, тому відрізок MB - відстань від точки M(5;4;12) до осі ординат.
Точка A(5;4;0) має такі координати, оскільки відрізок (перпендикуляр) MA опущений з точки M(5;4;12) паралельно осі Oz на площину xOy (тому абсциса і ордината не змінилися, а у площині xOy апліката z дорівнює нулю).
Точка B(0;4;0) має такі координати, оскільки відрізок (перпендикуляр) AB опущений з точки A(5;4;0) паралельно осі Ox на вісь Oy (тому ордината не змінилася, а на осі Oy абсциса x і апліката z дорівнюють нулю).
Знайдемо відстань між точками M(5;4;12) і B(0;4;0)за формулою:
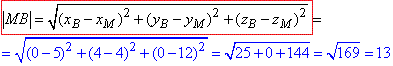
(Інша схема обчислень відрізка MB слідує із прямокутного трикутника ΔMAB за темою «35 прямі та площини в просторі», але тут показано метод координат).
Відповідь: 13 – Г.
Приклад 41.9 Знайти відстань від точки P(3;-6;8) до площини yOz.
А | Б | В | Г | Д |
3 | 4 | 6 | 8 | 10 |
Розв'язування: Відстань від точки до площини (в просторі) – це перпендикуляр опущений з точки на площину.
Проведемо перпендикуляр PK до площини yOz (паралельно вісі Ox) і поставимо точку K(0;-6;8), тут ордината і апліката не змінилися, а у площині yOz абсциса x дорівнює нулю.
Уважно погляньте на рисунок нижче, щоб переконатися в цьому.
Довжина відрізка PK і буде відстанню від точки P(3;-6;8) до площини yOz.
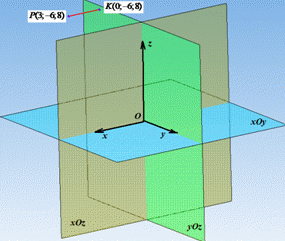
Знайдемо довжину відрізка PK: P(3;-6;8) і K(0;-6;8),
(Якщо відрізок паралельний деякій осі координат, то модуль різниці координат точок по цій осі й буде довжиною відрізка).
Відповідь: 3 – А.
В наступній статті навчимося складати рівняння кола, сфери, зводити їх рівняння до канонічного вигляду, знаходити радіус.
