Далі наведені готові відповіді до ЗНО тестів на тему 41. Координати. На попередньому уроці розглянули приклади на точки та довжини векторів, сьогодні будемо складати рівняння кіл та сфер та знаходити їх радіуси. З наведеними прикладами Ви повинні швидко розібратися, адже далі підуть уроки на зведення рівнянь кіл та сфер до канонічного вигляду та складніші завдання пов'язані з координатами.
Приклад 41.10 Скласти рівняння сфери, яка проходить через початок координат із центром у точці S(-1;2;-3).
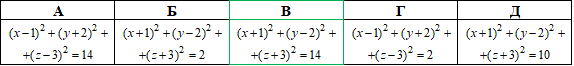
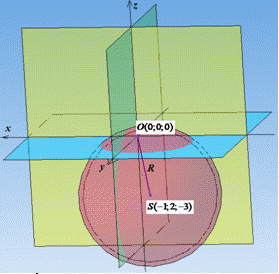
Розв'язування: Маємо точку на сфері, яка співпадає з центром координат і сам центр сфери. Побудуємо просторовий рисунок до завдання
Рівняння сфери з центром у точці S(a;b;c) і радіусом R:
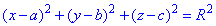
З умови відомо a=-1, b=2 і c=-3.
Оскільки точка S(-1;2;-3) - центр сфери, а точка O(0;0;0) (початок координат) належить сфері, то |OS|=R, звідси |OS|2=R2, обчислимо:
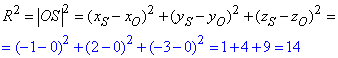
Отже, рівняння сфери має вигляд
(x+1)^2+(y-2)^2+(z+3)^2=14.
Відповідь: (x+1)2+(y-2)2+(z+3)2=14 – В.
Приклад 41.11 Вказати рівняння кола, яке на площині симетричне до кола (x-4)^2+(y+5)^2=9 відносно осі Oy.
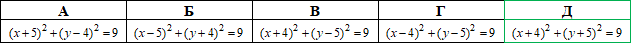
Розв'язування: Рівняння кола з центром у точці (a;b) і радіусом r:
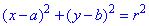
Маємо коло (x-4)2+(y+5)2=9 з центром A(4;-5) і радіусом r=3.
Якщо задане коло симетрично відобразити відносно осі Oy, то абсциси координат точок кола (та його центра) зміняться на протилежні, а ординати і геометричні розміри (радіус, довжина кола) залишаться без змін. Це добре видно з наступного рисунка кіл
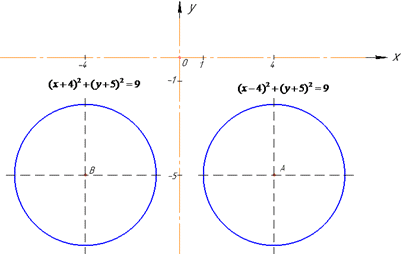
Тому при симетрії відносно осі Oy заданого кола отримаємо коло з центром B(-4;-5) та радіусом r=3.
Складаємо рівняння симетричного осі кола:
(x+4)2+(y+5)2=9.
Відповідь: (x+4)^2+(y+5)^2=9 – Д.
Приклад 41.12 Скласти рівняння кола з центром у точці C(5;-2), яке дотикається до осі ординат.
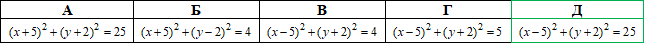
Розв'язування: Почнемо з теорії та пригадаємо, що рівняння кола з центром у точці (a;b) і радіусом r має запис:
(x-a)^2+(y-b)^2=r^2.
За умовою: a=5, b=-2.
Схематичний рисунок до завдання приведено далі
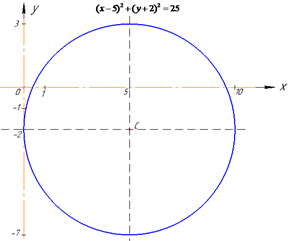
Радіус r знайдемо з умови, що задане коло дотикається до осі ординат (Oy). Оскільки в точці дотику радіус кола перпендикулярний до дотичної, то з цього випливає, що точка дотику кола до осі Oy має координати (0;-2) (абсциса x на осі ординат дорівнює нулю, а ордината дотику дорівнює ординаті центру кола).
Звідси отримуємо довжину радіуса кола: r=|5-0|=5 (тобто r=|x|=5, r^2=25).
Отже, рівняння заданого кола має вигляд:
(x-5)^2+(y+2)^2=25.
Відповідь: (x-5)^2+(y+2)^2=25 – Д.
Приклад 41.13 Скласти рівняння сфери з центром у точці A(-1;3;2), яке дотикається до площини xOy.
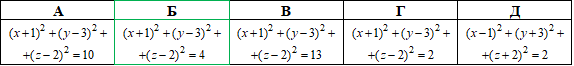
Розв'язування: Запишемо рівняння сфери з центром у точці A(a;b;c) і радіусом R:
(x-a)^2+(y-b)^2+(z-c)^2=R^2.
Рисунок сфери з площинами є підказкою до обчислень
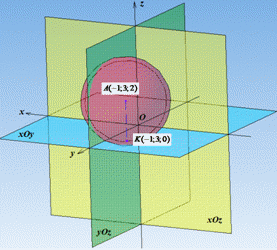
Радіус R знайдемо з умови, що задана сфера дотикається до площини xOy.
Оскільки в точці дотику радіус сфери перпендикулярний до дотичної, то з цього випливає, що точка дотику сфери з площиною xOy має координати (-1;3;0) (абсциса x і ордината y на площині xOy залишаються без змін, такі як у центра сфери, а апліката дотику z рівна нулю).
Базуючись на цьому можемо визначити радіус сфери:
R=|2-0|=2 (тобто R=|z|=2, R^2=4).
Складаємо рівняння сфери за вказаною на початку формулою:
(x+1)2+(y-3)2+(z-2)2=4.
Відповідь: (x+1)^2+(y-3)^2+(z-2)^2=4 – Б.
Приклад 41.14 Знайти координати центра кола x2-4x+y2+10y+20=0.
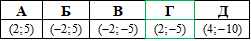
Розв'язування: Зведемо задане рівняння кола x^2-4x+y^2+10y+20=0 до канонічного вигляду (методом виділення повних квадратів):
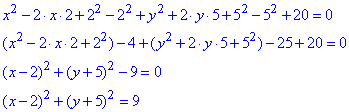
(x-2)^2+(y+5)^2=3^2.
Отримали канонічне рівняння кола (вигляду (x-a)^2+(y-b)^2=r^2), з якого маємо
A(2;-5) - координати центра кола, r=3 - радіус кола.
Наведемо рисунок досліджуваного кола в декартовій площині
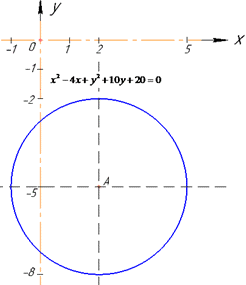
Відповідь: (2;-5) – Г.
Приклад 41.15 Знайти радіус сфери x2+y2-2y+z2+6z-6=0.
А | Б | В | Г | Д |
2 | 3 | 4 | 5 | 6 |
Розв'язування: Такого типу завдання полягають у зведенні до канонічної форми (методом виділення повних квадратів) самого рівняння сфери x^2+y^2-2y+z^2+6z-6=0, що само по соб не складно. Права частина тоді рівна квадрату сфери, а координати центра заховані в дужках.
Проведемо необхідні перетворення рівняння:
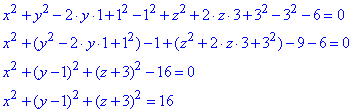
x^2+(y-1)^2+(z+3)^2=4^2.
Отримали канонічне рівняння сфери (вигляду (x-a)^2+(y-b)^2=r^2)), з якого маємо S(0;1;-3) - координати центра сфери, R=4 - радіус сфери.
Рисунок сфери має вигляд
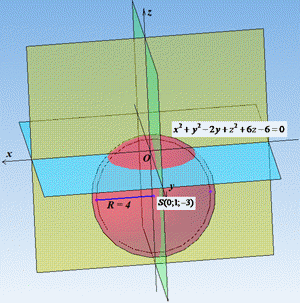
Відповідь: 4 – В.
Приклад 41.29 Знайти: 1) радіус R сфери;
2) площу S сфери (у відповідь записати S/π), заданої рівнянням x2+y2+z2-2x+2y-2=0.
Розв'язування: Зведемо задане рівняння сфери x^2+y^2+z^2-2x+2y-2=0 до канонічного виду (методом виділення повних квадратів):
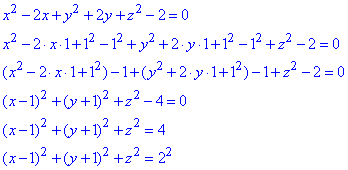
Вивели канонічне рівняння сфери (вигляду (x-a)^2+(y-b)^2+(z-c)^2=R^2), з якого маємо S(1;-1;0) - координати центра сфери, R=2 - радіус сфери.
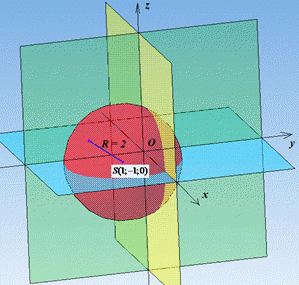
Знайти площу S сфери допоможе формула:
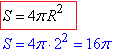
звідси S/π=16π/π=16.
Відповідь: 2; 16.
Приклад 41.30 Скласти рівняння кола з центром на осі ординат, яке проходить через точки A(-3;0), B(0;9). У відповідь записати довжину радіуса кола.
Розв'язування: Точка S - центр заданого кола, яке лежить на осі ординат (Oy), тому S(0;y).
Побудуємо допоміжний рисунок до завдання
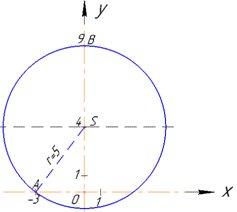
Оскільки задане коло проходить через точки A(-3;0), B(0;9), то |AS|=|BS|=r як радіуси кола (відстані від точки S(0;y) до точок A(-3;0) і B(0;9) відповідно), звідси |AS|2=|BS|2.
Складаємо рівняння квадратів модулів векторів
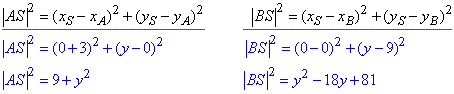
Прирівнявши останні дві залежності, знайдемо ординату y центра кола:
9+y^2=y^2-18y+81,
18y=81-9=72,
y=72:18=4.
S(0;4) - центр заданого кола.
Знайдемо його радіус r з умови (|AS|=|BS|=r):
r2=(|AS|2=9+42,
r^2=25,
r=5.
Будуємо рівняння кола :
(x-0)^2+(y-4)^2=5^2, або
x2+(y-4)2=25.
На цьому задача розв'язана, уважно перегляньте хід обчислень, адже такого типу завдань у Вас в навчанні буде багато.
Відповідь: 5.
Приклад 41.23 Установити відповідність між центрами і радіусами сфер (1–4) та їх рівняннями (А–Д). 
Розв'язування: Канонічне рівняння сфери має вигляд:
(x-a)^2+(y-b)^2+(z-c)^2=R^2, де C(a;b;c) - координати центра сфери;
R - радіус сфери.
У кожному з наведених завдань підставимо координати центра та радіус сфери у канонічне рівняння, розкриємо дужки і зведемо подібні доданки.
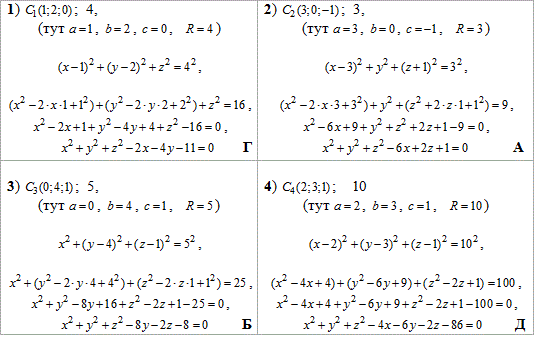
Розрахунки не складні, і всі деталі перетворень легко простежити з наведеної таблиці.
Задачі на знаходження координат точок, канонічних рівнянь кіл, сфер, обчислення відстані на площині та в просторі Ви повинні навчитися швидко та правильно розв'язувати, щоб успішно скласти ЗНО тести, вступні іспити та не мати проблем з навчанням у ВУЗах. Попереду ще дві публікації з готовими відповідями до задач на координати.


