Формула косинуса кута між векторами через скалярний добуток має вигляд
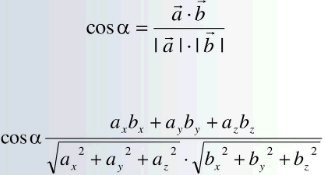
Верхня формула це векторний запис, нижня в координатній формі для просторових (тримірних) векторів.
Далі розглянемо приклади із ЗНО тестів на обчислення косинуса кута, та встановлення його градусної міри. Порядок розрахунків кута легко прослідкувати з наведених далі готових розв'язків. Завдання в першу чергу підійдуть учням 10-11 класів, останні приклади будуть повчальними і для студентів.
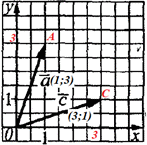
Приклад 42.17 Обчислити косинус кута між векторами a і c.
А | Б | В | Г | Д |
0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
Розв'язування: Випишемо координати початку O і кінця A вектора a:
O(0;0), A(1;3).
Обчислимо координати вектора a як різницю координат кінця A(1;3) та початку O(0;0):
A(1-0;3-0)=(1;3).
Обчислимо довжину (модуль) вектора a(1;3):
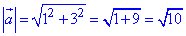
Такі ж операції проводимо для вектора с:
O(0;0), C(3;1).
Координати вектора c знаходимо через різницю координат кінця C(3;1) та початку O(0;0):
c(3-0;1-0)=(3;1).
Через корінь квадратний з суми квадратів координат знаходимо довжину (модуль) вектора c(3;1):
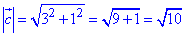
Скалярний добуток векторів a(1;3) і c(3;1):
a•c=1•3+3•1=6.
Обчислимо косинус кута φ між векторами a(1;3) і c(3;1) за формулою:
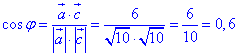
Відповідь: 0,6 – Д.
Приклад 42.13 Знайти кут між векторами a(1;0;-1) і b(0;-1;1).

Розв'язування: Кут φ між векторами a і b знайдемо за формулою:
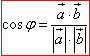
Обчислимо скалярний добуток векторів:
a•b=1•0+0•(-1)+(-1) •1=-1.
Визначимо довжину (модуль) векторів a,b:
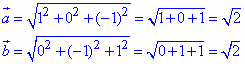
Знайдемо косинус кута φ між векторами a і b:
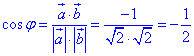
Визначимо кут φ між векторами через арккосинус:
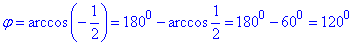
Отримали тупий кут в 120 градусів.
Відповідь: 1200 – Б.
Приклад 42.33 Дано |m|=2, |n|=3, а кут між векторами m і n дорівнює 120 градусів. Обчислити косинус кута між векторами m і m+n і знайти його значення з точністю до 0,01.
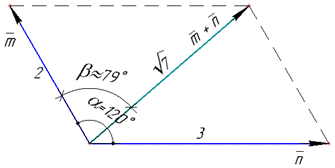
Розв'язування: Знайдемо скалярний добуток векторів m і n:
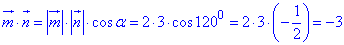 , отже отримали m•n=-3,
, отже отримали m•n=-3,
де α=120 – кут між векторами m і n, причому
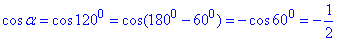
Знайдемо модуль (довжину) вектора m+n:
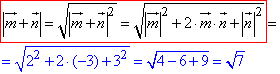
отже |m+n|=√7.
Знайдемо скалярний добуток векторів m і m+n:
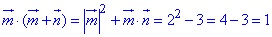
Обчислимо косинус кута β між векторами m і m+n, знайдемо його значення з точністю до 0,01:
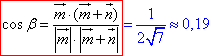
та сам кут β=arccos(0,19)=79.
Відповідь: 0,19.
Приклад 42.35 Знайти косинус кута між векторами -5a і 1/5•b з точністю до 0,01, якщо a(-1;1;4), b(1;0;-1).
Розв'язування: Знайдемо координати векторів -5a і 1/5•b:
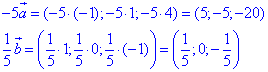
Знайдемо скалярний добуток векторів -5a і 1/5•b:
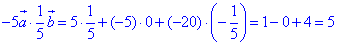 , отже отримали a•b=5.
, отже отримали a•b=5.
Знайдемо модуль (довжину) вектора -5a:
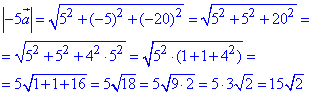
маємо|-5a|=15√2.
Знайдемо модуль (довжину) вектора 1/5•b:
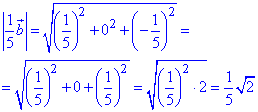
Знайдемо косинус кута φ між векторами -5a і 1/5•b з точністю до 0,01:
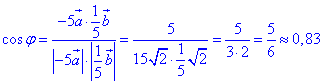
звідси φ=arccos(0,83)≈340.
Відповідь: 0,83.
Приклад 42.38 Дано трикутник MPK з вершинами в точках M(3;-2), P(1;4), K(2;-1). Знайти у градусах величину кута M.
Розв'язування: Знайдемо координати вектора MP:
MP=(1+3;4+2)=(4;6).
Знайдемо довжину (модуль) вектора MP(4;6):
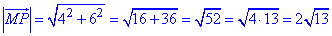
Знайдемо координати вектора MK:
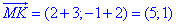
Знайдемо довжину (модуль) вектора MK(5;1):
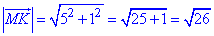
Знайдемо скалярний добуток векторів MP(4;6) і MK(5;1) рівний 26:
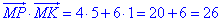
Обчислимо косинус кута M, тобто косинус кута між векторами MP і MK:
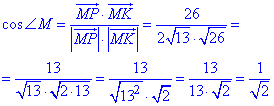
далі величину кута M через arccos():
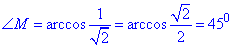
Побудуємо трикутник на трьох заданих векторах
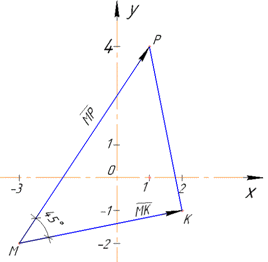
Відповідь: 45 градусів.
Приклад 42.40 Дано модулі двох векторів та кут між ними
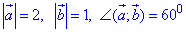
Знайти косинус кута між векторами a+b і a-b з точністю до 0,01.
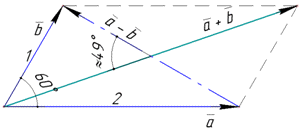
Розв'язування: Завдання ускладнюється тим що тут потрібно розраховувати модулі та скалярні добутки суми та різниці векторів, а для цього потрібно вивести більш складні формули. Уважно перегляньте хід обчислень, та запам'ятайте що для чого тут робили.
Визначимо скалярний добуток векторів a і b:
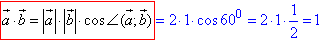
Довжину суми векторів a+b обчислимо за формулою:
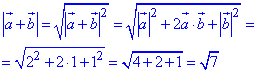
Модуль різниці векторів a-b знаходимо за правилом:
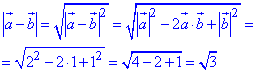
Скалярний добуток векторів a+b і a-b обчислимо за формулою різниці квадратів:
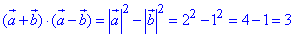
Знаходимо косинус кута φ між векторами a+b і a-b з точністю до сотих:
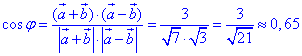
Знаючи що cos(φ)=0,65, на калькуляторі можемо визначити сам кут
φ=arccos(0,65)≈490.
Відповідь: 0,65.
Приклад 42.41 Знайти косинус кута між діагоналями паралелограма, побудованого на векторах a(3;2) і b(1;-2) з точністю до 0,01.
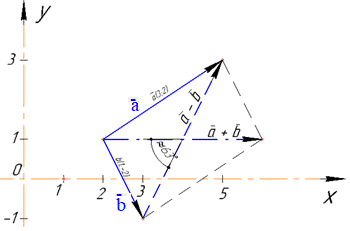
Розв'язування: Діагоналями паралелограма, побудованого на векторах a і b (згідно з правилом додавання і віднімання векторів) будуть вектори a+b і a-b.
Визначаємо координати вектора a+b:
a+b=(3+1;2-2)=(4;0).
З рисунку бачимо, оскільки вектор a+b має координати (4;0), то цей вектор розташований паралельно осі абсцис (Ox).
Знайдемо довжину a+b:
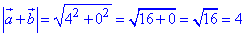
Координати вектора a-b:
a-b=(3-1;2+2)=(2;4).
Обчислюємо довжину (модуль) вектора a-b:
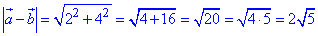
Скалярний добуток векторів a+b і a-b рівний різниці квадратів:
(a+b)(a-b)=4•2+0•4=8.
Знаходимо косинус кута φ між діагоналями паралелограма (векторами a+b і a-b) з точністю до сотих:
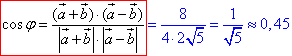
звідси φ=arccos(0,45)≈630.
Відповідь: 0,45.
Приклад 42.42 Знайти косинус кута між діагоналями паралелограма, побудованого на векторах a=4m+2n і b=4m+n з точністю до 0,01, якщо |m|=|n|=1, φ=∠(m;n)=60.
Розв'язування: Для ілюстрації, що шукаємо та який вигляд мають вектори на площині наведемо рисунок
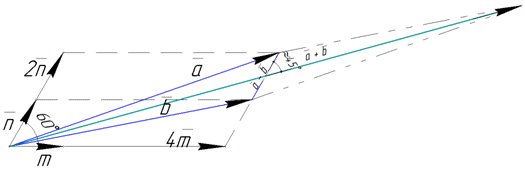
Діагоналями паралелограма, побудованого на векторах a і b (згідно з правилом додавання і віднімання векторів) будуть вектори a+b і a-b, де
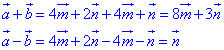
Знайдемо скалярний добуток векторів m і n:
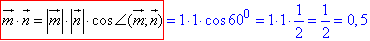
Знайдемо модуль суми векторів a+b=8m+3n:
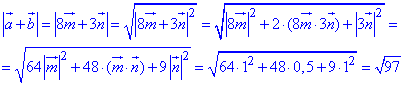
Знайдемо модуль вектора a-b=n:
|a-b|=|n|=1.
Обчислимо скалярний добуток векторів a+b=8m+3n і a-b=n:
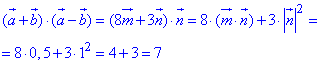
Визначимо косинус кута α між діагоналями паралелограма (векторами a+b і a-b) з точністю до сотих:
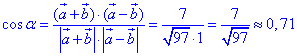
звідси α=arccos(0,71)≈450.
Відповідь: 0,71.
Попереду ще сотні готових відповідей із ЗНО підготовки, тому вчіться та економте грошенята на репетиторах.
Додавайте сайт в закладки та діліться з друзями у соцмережах!


