Для вивчення теми "Вектори" + успішного проходження зовнішнього незалежного тестування нами розв'язані типові тестові завдання. За шпаргалку можете використовувати при побудові векторів наведені далі схеми.
Cума векторів за правилом трикутника та паралелограма
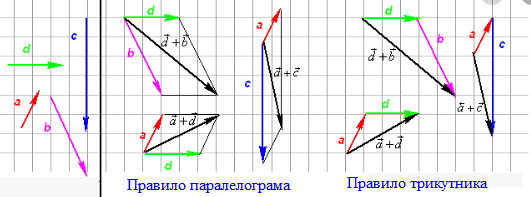
Схема побудови різниці векторів за правилом трикутника та паралелограма
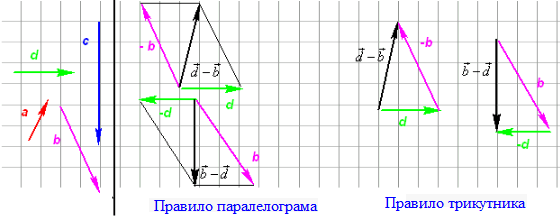
Відповідні формули скалярного добутку векторів, довжини та розрахунку кутів виділені в поясненнях до прикладів червоною рамкою. Для економії часу завантаження сторінки, всюди де йде мова про вектори над ними потрібно писати стрілку 
, хоча в тексті ми використовували позначення "вектор а". Це зроблено для покращення індексації сторінки та щоб швидше знайти завдання в пошуку, Ви прирозв'язуванні дотримуйтеся правил ().
Приклад 42.28 Установити відповідність між векторами (1–4) та їх координатами (А–Д).
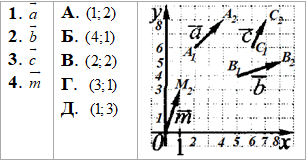
Розв'язування: Знайдемо координати початку та кінця заданих векторів, тоді по них запишемо координати цих векторів:
1. A1(2;6) – початок вектора a,
A2(4;8) – кінець вектора a,
A(4-2;8-6)=(2;2) В.
2. B1(5;4) – початок вектора b,
B2(8;5) – кінець вектора b,
B(8-5;5-4)=(3;1) Г.
3. C1(6;6) – початок вектора c,
C2(7;8) – кінець вектора c,
c(7-6;8-6)=(1;2) А.
4. O(0;0) – початок вектора m,
M2(1;3) – кінець вектора m,
M(1-0;3-0)=(1;3) Д.
Отже, маємо 1 – В, 2 – Г, 3 – А, 4 – Д.
Приклад 42.3 Дано вектори a і b. Який з наведених векторів дорівнює різниці a-b?
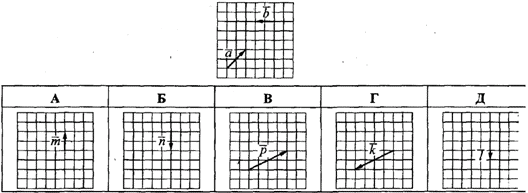
Розв'язування: Відняти вектор a від вектора b означає, що до вектора a треба додати вектор -b (протилежний за напрямком вектору b).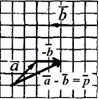
Додавання робитимемо за правилом трикутника:
від кінця вектора a відкладаємо вектор -b, далі суму векторів отримуємо, з'єднавши початок вектора a з кінцем вектора -b, в результаті отримаємо вектор p, тобто
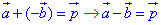
Відповідь: p – В.
Приклад 42.1 Дано паралелограм ABCD. O – точка перетину діагоналей.
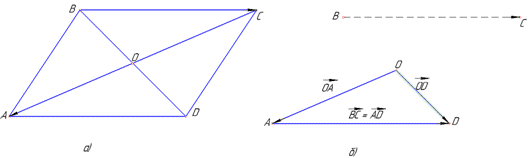
Який з наведених векторів дорівнює сумі BC+OA?
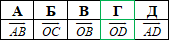
Розв'язування: Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні, а діагоналі в точці перетину діляться навпіл. У паралелограма ABCD сторони будемо позначати векторами із заданим напрямком . Звідси слідує, що вектори BC=AD, тобто рівні, бо колінеарні, співнапрямлені та рівні по модулю (довжині). Додавати вектори будемо за правилом трикутника (дивись рисунок б):
від кінця вектора OA відкладаємо вектор AD (він же BC), далі суму векторів отримуємо, з’єднавши початок вектора OA з кінцем вектора BC, в результаті отримаємо вектор OD, тобто OA+BC+OD,
BC+OA=OD.
Відповідь: OD – Г.
Правило трикутника, та як правильно будувати лінійні комбінації векторів Ви повинні поступово вивчити, та пам'ятати, як відкладати вектори,знаходити їх суму та різницю.
Приклад 42.2 Дано вектор a. Який з наведених векторів дорівнює -2/3a?
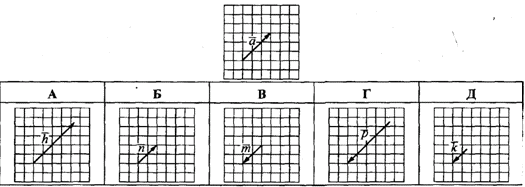
Розв'язування: Перш за все дамо загальні правила масштабування векторів:
Множення вектора на число λ:
якщо |λ|>1, то вектор розтягнули у λ разів;
якщо |λ|<1, то вектор стиснули у λ разів;
якщо |λ|=1, то модуль (довжина) векторане змінилася;
якщо λ<0, то напрямок вектора a змінили на протилежний.
Отже,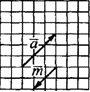 
при множенні вектора на число λ=-2/3 (тут -1< λ <0) вектор -2/3a змінив напрямок і стиснули у 2/3 рази, тобто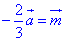 
(кількість клітинок по горизонталі і вертикалі зменшили у 3 рази, а потім збільшили у 2 рази, рисунок В).
Відповідь: m – В.
Приклад 42.4 O – точка перетину медіан трикутника ABC.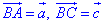 
Виразити вектор OB через вектори a і c.
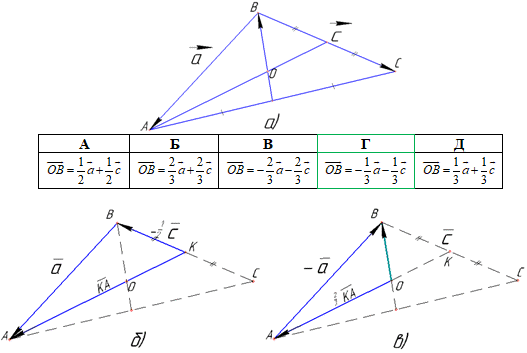
Розв'язування: Медіана AK трикутника ABC – відрізок, який виходить з вершини A трикутника і ділить протилежну сторону BC навпіл, тобто BK=KC.
Розглянемо трикутник ABK (рисунок а), у якого сторони є векторами:
BA=a, KB=-c/2 (тут BK=BC/2 і KB=-BK=-BC/2=-c/2).
За правилом трикутника додавання векторів знайдемо вектор AK:
KB+BA=KA, -c/2+a=KA, звідси KA=a-c/2.
Медіани трикутника ABC в точці перетину O діляться у відношенні 2:1, починаючи від вершини. Тобто KA=KO+OA і OA=2KO, звідси AO=2KA/3.
Розглянемо трикутник ABO (рисунок б), у якого сторони є векторами: AB=-a (протилежний до вектора a), OA=2/3•KA (за властивістю перетину медіан ΔABC).
За правилом трикутника додавання векторів знайдемо вектор OB:
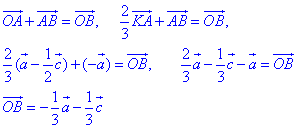
Відповідь: -1/3•a-1/3•c – Г.
Приклад 42.23 Дано квадрат ABCD. Який з наведених векторів дорівнює сумі AC+BD?
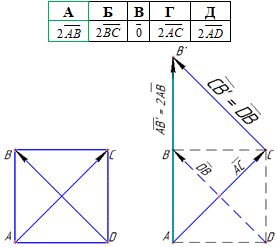
Розв'язування: У квадрата ABCD сторони і діагоналі будемо векторами із заданим напрямком позначати. Вектор DB паралельно перенесемо так, щоб його початок співпав з кінцем вектора AC, тоді отримаємо йому рівний вектор CB', тобто DB=CB' (при паралельному перенесенні напрямок і довжини векторів (їх координати) залишаються незмінними).
Додавати вектори будемо за правилом трикутника (дивись рисунок): від кінця вектора AC відкладаємо вектор DB (він же CB'), далі суму векторів отримуємо, з'єднавши початок вектора AC з кінцем вектора CB, в результаті отримаємо вектор AB' (він же 2AB, оскільки точка B перейшла в точку B' на таку ж відстань і напрямок як точку D перенесли в точку C), тобто
AC+CB'=AB', AC+DB=2AB.
Відповідь: 2AB – А.
Приклад 42.24 Вектор OA лежить на осі Oz прямокутної декартової системи координат у просторі (див. рисунок), і його початок збігається з початком координат.
Визначити координати вектора OA, якщо його довжина дорівнює 3.
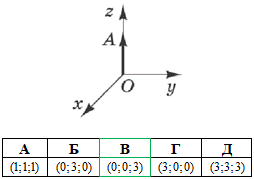
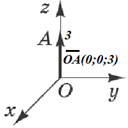
Розв'язування: За умовою завдання початок вектора OA збігається з початком координат, тому має координати O(0;0;0). Сам вектор OA лежить на осі Oz, тому його кінець, точка A, також лежить на осі Oz, тобто A(0;0;z) (на осі аплікат Oz абсциса x і ордината y дорівнюють 0).
Оскільки |OA|=3 (за умовою), то |z-0|=3, звідси z=3. Координата z>0 оскільки вектор OA напрямлений в додатному напрямку осі Oz.
Записуємо координати вектора
A(0;0;3).
Відповідь: (0;0;3). – В.
Попереду декілька статей на довжину (модуль) вектора, суми та різниці векторів, обчислення скалярного добутку та кутів між векторами. Готові приклади допоможуть Вам швидко пройти теоретичний матеріал та вивчити формули.
