Лінійна залежність і незалежність векторів. Розклад вектора за базисом

З даного матеріалу Ви навчитеся розкладати вектор за базисом, перевіряти вектори на лінійну незалежність, знаходити вимірність простору. Почнемо вивчати з самого основного, що потрібно знати.
Нехай нам задано вектори з -вимірного векторного простору, а також деякі дійсні числа
Вектор називається лінійною комбінацією векторів
Вектори бувають лінійно залежними або незалежними. Ці властивості визначають на основі наступних правил:
1) Вектори називаються лінійно залежними, якщо знайдуться такі дійсні числа , одночасно не рівні нулю, при яких справджується рівність

2) Якщо рівність виконується лише за умови, що то вектори називаються лінійно незалежними.

На практиці лінійну незалежність векторів перевіряють із умови, що визначник складений із координат векторів відмінний від нуля. Для прикладу, якщо маємо три вектори з простору , то для підтвердження їх лінійної незалежності визначник

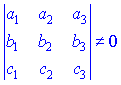
не має бути рівний нулеві. В іншому випадку вектори будуть лінійно залежними.
З властивостей визначників випливає, що вектори будуть лінійно залежні тоді і тільки тоді, коли хоча б один з них є лінійною комбінацією інших.

Вимірність простору - це максимальна кількість лінійно незалежних векторів, що може бути у ньому. Будь-яку сукупність лінійно незалежних векторів -вимірного лінійного простору називають його базисом.

Будь-який векторз єдиним способом може бути зображений у вигляді лінійної комбінації векторів базису. Якщо - базис лінійного простору , то - розклад вектора за базисом ,
- координати вектора у цьому базисі.
Задачі розкладу вектора займають важливе місце в курс вищої математики, і потрібні не менше за відшукання базису лінійного простору.

Алгоритм розкладу вектора за базисом

1. Записати рівність у матричній формі. Вектори подати у вигляді матриць-стовпців.
2. Матричне рівняння записати у вигляді системи лінійних алгебраїчних рівнянь. Розв'язати одержану систему.
3. Записати розклад вектора за базисом .
Для цього в рівність замість підставити розв'язки системи рівнянь.

Приклад 1. Записати розклад вектора за базисом

Розв'язок. Скористаємося формулою розкладу вектора

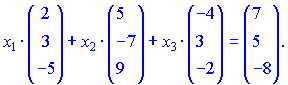
Дане рівняння записуємо у вигляді системи лінійних рівнянь

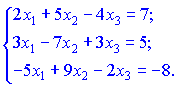
Розв'язком цієї системи
Обчисювати систему рівнянь моете методом Гауса або Крамера, що Вам простіше і швидше.
Отримані значення підставляємо в рівняння розкладу, в результаті отримаємо - розклад вектора в базисі
Як бачите обчислення не складні, наведена інструкція допоможе Вам розв'язати подібні задачі. Завдання розкладу за базисом векторів рівносильне до обчилення систем лінійних рівнянь. А от встановлення векторів базису, переходу між базисами - куда складніші задачі, які Ви навчитеся розв'язувати з наступних уроків.