Означення першої важливої границі: границя відношення синуса до аргумента, коли він прямує до нуля рівна одиниці
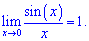
Наслідки першої особливої границі
Варто зазначити, що не всі границі, що містять тригонометричні функції слід зразу зводити до першої особливої границі. Все залежить, як входить функція, та чи можна звести під потрібну формулу. Плюс тригонометричні функції, коли ті прямують до нуля завжди можна замінити еквівалентними нескінченно малими виразами, але це вже інша техніка обчислення границь.
Слід відмітити, що на практиці в якості аргумента може виступати не тільки змінна, а й елементарна функція, поліном, чи будь-яка складна функція, що прямує до нуля. Про це Ви повинні пам'ятати і лише в таких випадках зводити обчислення під правило першої важливої границі. Важливо щоб змінна в тригонометричній функції прямувала до нуля, наприклад:
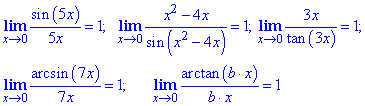
В наведених границях усі аргументи тригонометричних функцій прямують до нуля.
А от наступна границя знайдена неправильно
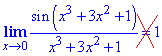
У Вас виникне запитання, Чому так? А тому що вираз x3+3x^2+1 не прямує до нуля, коли змінна x прямує до нуля.
Спробуйте самостійно знайти вказану границю, а ми вкінці статті звіримо відповіді.
Часто швидшим методом знаходження границі є заміна функцій еквівалентними (~) нескінченно малими величинами
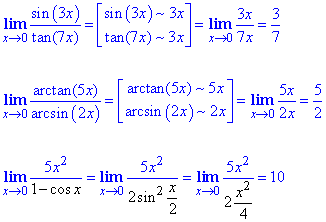
що є правильно, доцільно та виправдано в плані часу затраченого на розрахунки.
Але зараз в нас задача, навчити Вас розв'язувати завдання на першу границю, тому переходимо до підготовлених відповідей.
Приклади на першу важливу границю
Приклад 1 Знайти ліміт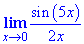 
Обчислення: Якщо бачите в границі синус, то з цього не завжди слідує про необхідність зводити до першої важливої границі
Спершу підставимо 0 в вираз під знаком ліміта (робимо це в голові не записуючи в зошит, або можете записати яку особливість дістанемо):
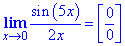
Отже, маємо особливість типу 0/0, її можна вказати при розв'язуванні, все залежить від ВУЗу та вимог оформлення границь. Дріб під знаком границі схожий на першу важливу границю, але це не вона.
Для зведення під формулу першої границі необхідно в штучний спосіб у знаменнику отримати такий самий вираз, який мститься під синусом.
На практиці виглядає це наступним чином:
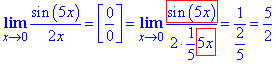
Обведений вираз в нас рівний першій границі, все решта множник при ній.
Аналогічно отримаєте якщо замінити синус еквівалентним нескінченно малим значенням sin(5x)~5x.
Відповідь: 5/2.
Приклад 2 Обчислити границю дробу
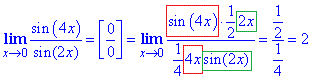
Обчислення: Чисельник та знаменник домножили на змінну, а далі штучно ввели множники які фігурують як аргументи синусів. Таким чином отримали дві чудові границі та сталі, які вкінці спростили.
Відповідь: 5/2.
Приклад 3 Знайти границю
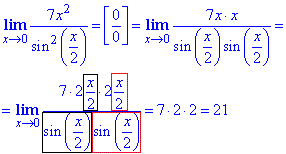
Обчислення: Тут штучно звели вираз в чисельнику під аргумент синуса в чисельнику та виразили першу визначну границю, після цього обчислення спростилися до множення трьох чисел.
Відповідь:21.
Приклад 4 Знайти границю
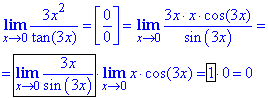
Обчислення: Проста підстановка показує, що маємо невизначеність виду 0/0, яку потрібно розкрити. Розпишемо в знаменнику tan(3x) за тригонометричною формулою tan(3x)=sin(3x)/cos(3x), а в чисельнику виділимо множник 3x. Таким чином отримаємо першу важливу границю помножену на границю від x•cos(3x), яка рівна нулю.
Тут не прийшлось шукати додаткові множники, проте розкриття невизначеності показало, що можна отримати в результаті як нуль, так і безмежність, якщо б мали обернений вираз.
Відповідь:0.
Приклад 5 Обчислити границю
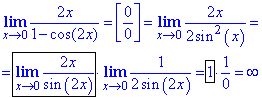
Обчислення: Невизначеність типу 0/0 розкриваємо шляхом виділення першої важливої границі, тільки цього разу вираз, що залишається в другій границі прямує до безмежності при змінній прямуючій до нуля.
Тут використали тригонометричну формулу
1-cos(2x)=2sin2(x).
Відповідь: ∞.
Бувають приклади коли застосування еквівалентних нескінченно малих величин є ефективнішим в плані простоти обчислень, ніж зведення під першу важливу границю.
Приклад 6 Знайти границю
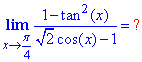
Обчислення: Легко переконатися, що чисельник і знаменник прямують до нуля. Для знаходження границі використаємо розклади функцй cos(x), tan2(x) по степенях при x→π/4.
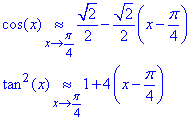
Підставимо отримані значення в границю
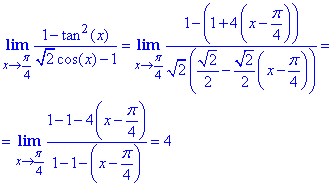
Відповідь:4.
Приклад 7 Знайти границю
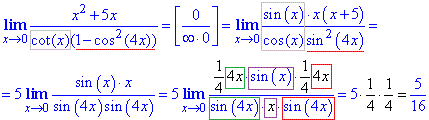
Обчислення: Тут сot(x) розписали за формулою ctg(x)=cos(x)/sin(x). Далі спростили доданки, які не вносять вкладу в границю. І наостанок в чисельнику та знаменнику ввели множники, які дозволили в одному прикладі виділити три перші особливі границі. Всі решта сталі псля множення дали значення границі.
Відповідь: 5/16.
Приклад 8 Знайти границю
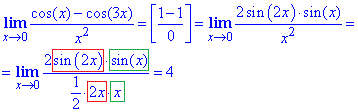
Обчислення: Отримали дещо іншу невизначеність від розглянутих раніше, яку розкрили за допомогою тригонометричної формули
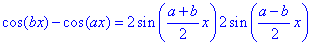
В результаті отримали добуток двох перших особливих границь.
Відповідь: 4.
Приклад 9 Обчислити границю
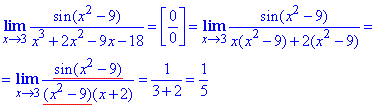
Обчислення: Розкрити невизначеність типу 0/0 вдалось завдяки виділенню в знаменнику множника ,який фігурує як аргумент синуса в чисельнику дробу. Тут можна було виконати заміну змінних y=x-3, що ви можете перевірити самостійно і подібним чином звести розв'язування до першої важливої границі.
Відповідь: 1/5.
Приклад 10Обчислити границю
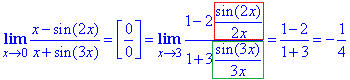
Обчислення:Підстановка 0 показує, що маємо невизначеність 0/0, яку необхідно розкрити. Щоб звести дріб під першу особливу границю в чисельнику та знаменнику виносимо аргумент та добиваємося, щоб дроби, що містить синуси мали в знаменнику однакові аргументи як у синусів.
Відповідь: -1/4.
Приклад 11 Обчислити границю
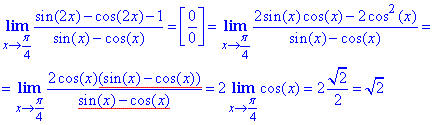
Тут використали тригонометричні формули синуса подвійного кута sin(2x)=2sin(x)cos(x) та залежність 1+cos(2x)=2cos2(x)
Відповідь: √2.
Приклад 12 Обчислити границю
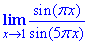
Розв'язування: Першу особливу границю тут застосовувати напряму неможна, оскільки аргументи πx, 5πx не прямують до нуля при x=1. Тому необхідно виконати заміну змінних x-1=y, тоді при x→1 змінна y→0, що й необхідно для застосування 1 особливої границі. Далі врахували періодичність тригонометричних функцій та штучно ввели потрібні множники
Відповідь: 1/5.
Приклад 13Обчислити границю
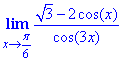
Розв'язування: Вводимо заміну змінних x-π/6=y, далі розписавши функції використовуємо тригонометричну форму представлення різниці косинусів через добуток відповідних синусів. Решта обчислень полягає в виділенні першої важливої границі
Відповідь: -1/3.
Приклад 14 Знайти ліміт функції
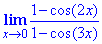
Розв'язування: Оскільки, взяті окремо границі чисельника 1-cos(2x) та знаменника 1-cos(3x) прямують до нуля коли x прямує до нуля, то маємо особливість типу нуль розділити на нуль. Розкриємо невизначеність за допомогою першої визначної границі. Для цього використаємо наступні тригонометричні формули, що, перейти від косинусів до синусів
1-cos(2x)=2sin2(x);
1-cos(3x)=2sin2(3x/2).
З врахуванням формул вище, обчислимо границю функції
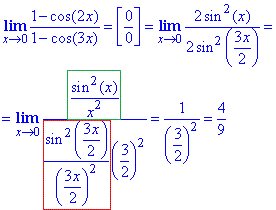
Відповідь: 4/9.
Приклад 15 Знайти ліміт функції
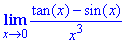
Розв'язування: Підстановка в уяві ургумента рівного нулю в чисельник і знаменник дає особливість типу нуль розділити на нуль 0/0. Щоб розкрити невизначеність розпишемо тангенс, а далі за тригонометричними формулами замінимо 1-cos(x)=2sin2(x/2). Далі штучним введенням потрібного множника зводима під правило першої визначної границі.
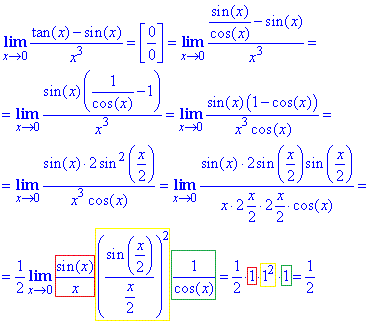
Відповідь:1/2.
При обчисленнях Вам часто доводиться використовувати різні тригонометричні формули, які дозволяють перейти до синусів. Ми для Вас їх згрупували, можете їх скопіювати, роздрукувати та використовувати в навчанні.
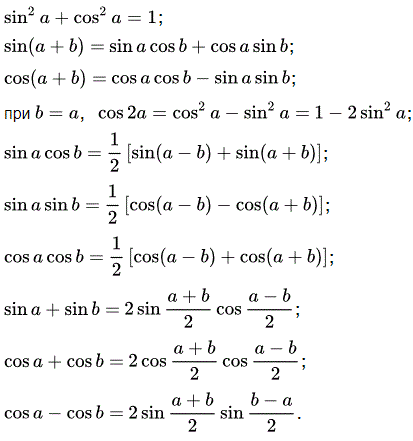
І на початку ми казали що границя 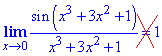подібна до першої, але не рівна 1, через те що аргумент не прямує до нуля. Якщо підставити нуль в чисельник та знаменник, то отримаємо limit=sin(1). Якщо Ви до цього прийшли самостійно, та можете розв'язувати наведені завдання без допомоги, то практикуми та екзамени здасьте на відмінно.
На цьогму розв'язування прикладів на першу важливу границю не закінчується, більше готових відповідей Ви можете знасти на сусідніх сторінках сайту.
